铁路双线连续钢桁梁桥竖向有载自振频率研究

任剑莹，李文平，苏木标

(1.石家庄铁道大学工程力学系，石家庄 050043;2.石家庄铁道大学土木工程学院，石家庄 050043;3.石家庄铁道大学大型结构健康诊断与控制研究所，石家庄 050043)

1 概述

列车上桥后，由桥梁恒载以及作用在桥梁上的活载一起确定的结构固有自振频率称为有载自振频率。当作用在桥梁上活载激励力的频率——强迫振动频率与桥梁的有载自振频率吻合时，将发生共振现象［1］。文献［2］中也指出:当列车以一定速度匀速通过桥梁时，具有相同长度的多辆车辆的轴重荷载对桥梁的动力作用相当于一个周期性荷载，如果这个周期性荷载的频率的整数倍与桥梁某一竖向有载自振频率相等时，车-桥系统将出现竖向共振现象，且共振峰值将随列车速度的提高而增大。

本文将在文献［3］的基础上，推导铁路双线连续梁桥的竖向有载自振频率的计算公式，并计算2列20辆相同参数的提速客车同时通过双线连续钢桁梁桥时，车-桥系统的竖向有载自振频率，得出一些有益的结论。

2 铁路双线连续梁桥竖向有载自振频率计算公式推导

2.1 车－桥系统计算模型

设列车自桥梁左侧上桥通过桥梁时(t时刻)，列车的第KL到第ML个轮对在桥上，车-桥系统的计算模型如图1所示。同样设列车自右侧上桥通过桥梁时(t时刻)，列车的第KR到第MR个轮对在桥上，计算模型如图2所示。两相邻车辆间的联接器设为铰接;每辆车有4个轴，车体理想化为具有沉浮自由度和点头自由度的刚体;转向架的质量平均分配给车体和4个轮对;车辆的两系竖向悬挂弹簧看作串联线性弹簧，刚度系数用等效刚度系数代替［4］;各个轮对与钢轨始终保持接触，保证轮对的竖向位移与相应位置的桥梁的挠度始终保持一致。车辆的计算模型如图3所示。

图1 列车自左侧上桥时车-桥系统计算模型

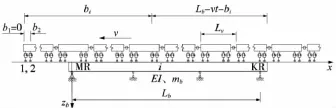
图2 列车自右侧上桥时车-桥系统计算模型

图3 车辆计算模型

2.2 车-桥系统振动方程

由达朗贝尔原理和车辆的计算模型可得出每辆车的振动方程为［2］

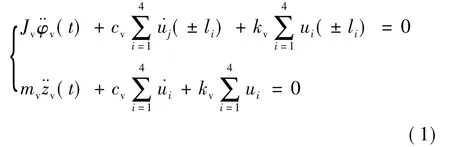
其中:ui为车辆第i轴悬挂弹簧的变形;kv、cv分别为车辆每一轴悬挂弹簧的等效刚度系数和等效阻尼系数;Jv、mv分别为车体的点头惯性矩和质量;φv、zv分别为车体的点头位移和沉浮位移;li的意义见图3所示。

桥梁的振动方程为

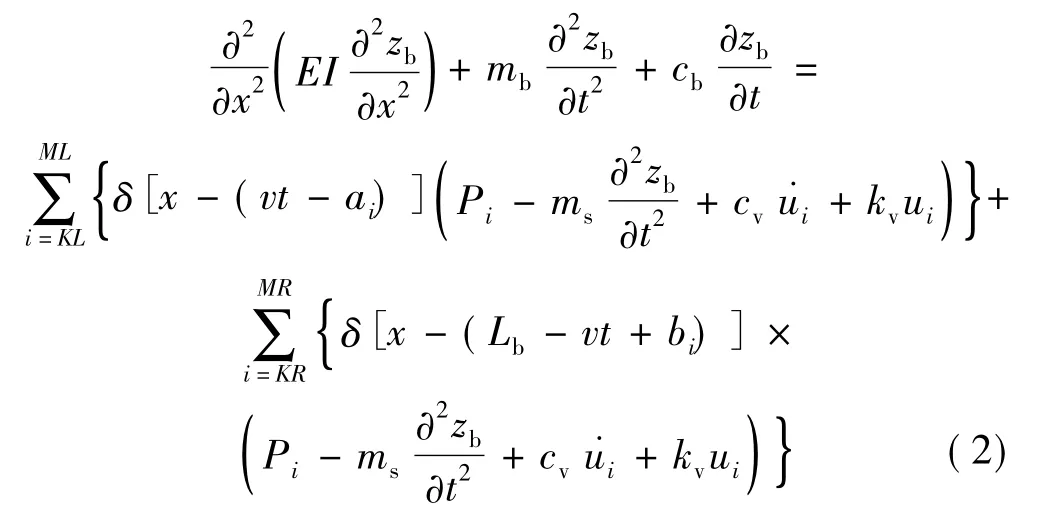
其中:EI、mb和cb分别为桥梁的竖向抗弯刚度、单位长度质量和阻尼系数;Pi为列车第i轮对的静轴重;ms为列车第i轮对的簧下质量;cv、kv分别为列车第i轮对悬挂弹簧的等效阻尼系数和等效刚度系数;ai、bi分别为左侧上桥列车和右侧上桥列车的第i轮对距第1轮对的距离(列车最前端的轮对为第1轮对);ui为列车第i轮对悬挂弹簧的变形;v为列车的行驶速度;δ(x－η)是 Dirac函数。

将式(1)和式(2)联立，可得车-桥系统的振动方程。由阵型叠加法，整理后可得车-桥系统的质量矩阵和刚度矩阵，再由Jacobi方法计算出车-桥系统的竖向有载自振频率，具体求解方法详见文献［3］。

3 铁路双线栓焊下承式连续钢桁梁桥竖向有载自振频率计算

3.1 计算结果

先计算桥梁的前5个竖向无载自振频率及其相应的阵型。由于本文只研究桥梁的竖向振动，故桥梁的有限元计算模型等效为一个竖向平面内的计算模型，采用平面杆单元，主桁每两个结点间的杆件为一个单元，单元的刚度和质量均为等效刚度和等效质量，所有结点均为铰接，全桥共计93个杆单元，如图4所示。

图4 3×64 m单线铁路栓焊下承式连续钢桁梁桥计算模型

当2列有20辆相同参数的提速客车分别以160 km/h的速度自桥梁的两端同时上桥，通过3×64 m双线铁路栓焊下承式连续钢桁梁桥时，自列车的第一轮对上桥时开始计时，计算得到该桥第1、第2、第3、第4、第5竖向有载自振频率，由于篇幅所限本文仅列出了前3个竖向有载自振频率随时间变化的曲线，如图5～图7所示。

图5 铁路双线连续钢桁梁桥第1竖向有载自振频率

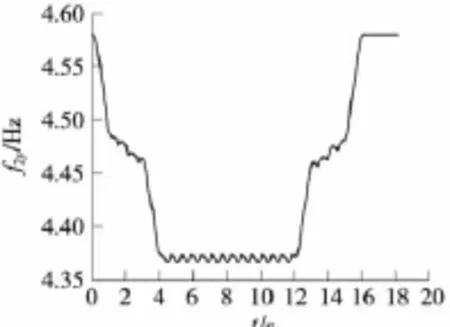
图6 铁路双线连续钢桁梁桥第2竖向有载自振频率

图7 铁路双线连续钢桁梁桥第3竖向有载自振频率

3.2 结果分析

通过对该3跨双线连续钢桁梁桥的计算，得出与文献［3］和文献［6］相似的结论:列车自桥梁两端同时上桥时，桥梁的竖向有载自振频率就开始逐渐减小;当桥上满布车辆时，桥梁的竖向有载自振频率开始呈周期性变化;当列车开始下桥(由车辆满布全桥到车辆逐步出桥)时，桥梁的竖向有载自振频率开始逐渐增大，直至列车全部离开桥梁，桥梁的竖向有载自振频率恢复到竖向无载自振频率。

由图5～图7可见，变化曲线在下降阶段和上升阶段，有一个周期变化的阶段。该阶段是2列列车开始会车，恰好桥上满布车辆时，和两列列车错车后，开始下桥时，竖向有载自振频率的变化规律，在图6和图7中比较明显。

表1列出了该连续梁桥的前5个竖向有载自振频率的变化范围及相应的竖向无载自振频率值。同时列出了文献［3］的结论。由表1及图5～图7可见，3×64 m铁路双线下承式连续钢桁梁桥的竖向有载自振频率与竖向无载自振频率比较，偏差值都比相同跨度单线桥的偏差大，双线最大偏差为6.042 5%，单线最大偏差为3.260 4%。双线有载自振频率的平均值和单线有载自振频率的平均值相差不多，最大差值为0.166 9 Hz。双线桥梁竖向有载自振频率周期变化的范围比较小，最大差值为0.013 7 Hz＜0.1 Hz，因此铁路双线连续钢桁梁桥的竖向有载自振频率可以取其平均值代替。

4 结论

通过以上计算和分析，得到以下几点结论:

(1)所得铁路双线连续钢桁梁桥的竖向有载自振频率的变化规律与简支梁桥［6］以及单线铁路连续钢桁梁桥［3］的竖向有载自振频率的变化规律相似。

表1 铁路连续钢桁梁桥竖向有载自振频率概况

(2)3×64 m铁路双线下承式连续钢桁梁桥的前5个竖向有载自振频率偏离其竖向无载自振频率的差值最小为1.310 1%，最大为6.042 5%，因此，在实际应用时，必须计算桥梁相应的竖向有载自振频率值。

(3)该双线连续钢桁梁桥满布车辆时，竖向有载自振频率呈周期性变化，但是变化幅度比较小，最大仅为0.013 7 Hz。因此，实际计算桥梁的竖向有载自振频率时，可取其平均值代替。

［1］中华人民共和国铁道部.铁运函［2004］120号 铁路桥梁检定规范［S］.北京:中国铁道出版社，2004.

［2］Li Jianzhong，Su Mubiao.The resonant vibration for a simply supported girder bridge under high-speed trains［J］.Journal of Sound and Vibration，1999，224(5):897-915.

［3］任剑莹，苏木标，李文平，梁滨波.铁路连续梁桥竖向有载频率研究［J］.铁道学报，2005，27(5):111-116.

［4］王福天.车辆动力学［M］.北京:中国铁道出版社，1983.

［5］蒋存煜.有限元基础［M］.北京:清华大学出版社，1984.

［6］苏木标，李建中，梁志广.铁路简支梁桥竖向有载频率研究［J］.铁道学报，2001，23(2):76-80.