基于FP-tree目录分割自适应算法

陆 楠，杜文峰，梁正平

深圳大学计算机与软件学院，深圳 518060

基于FP-tree目录分割自适应算法

陆 楠，杜文峰，梁正平

深圳大学计算机与软件学院，深圳 518060

研究面向顾客的商业智能目录分割问题，要求顾客对收到的目录至少有兴趣度t，并评估满足最小兴趣度的顾客数量.为优化评估效果，构建频繁模式树结构FP-tree存储顾客数据库，给出MCC-CS算法解决目录分割问题，该算法使用树深度遍历法选择目录产品.经验证，该算法能够获得更好的商业目标.

数据挖掘;目录分割;顾客覆盖;频繁模式树;自适应算法

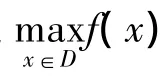
分割问题［3-4］是一类基于微观经济观点的经典商业智能优化问题，包括市场分割和目录分割［3］.本研究讨论的目录分割问题可描述为:企业将定制目录发送给顾客，使顾客了解企业产品达到促销效果.该问题有3个要求［3-4］:① 目录需大小适中.对传统企业来说，若目录太大则设计、印刷和邮寄等成本加大，对于电子商务公司来说，目录太大会分散顾客注意力，使顾客产生厌倦情绪.反之，若目录太小，则不足以产生促销效果;② 目录中包含的商品需具有代表性，使顾客能够对其感兴趣，从而促进非目录商品的销售.一旦顾客通过目录被吸引到实体店，就有可能购买非目录中的产品;③企业应针对不同顾客制定不同目录.仅对所有顾客制定1个目录是不明智的，并非所有顾客都关心同样的商品.然而限于成本也不能为每个顾客都制定一个特定目录.因此，企业通常将顾客划分为k个簇，再针对每个簇制定相应的目录，使促销效果最佳.由此可见，顾客目录分割问题也是一个NP(non-deterministic polynomial)完全问题［3］.

作为商业智能目录分割问题，从市场营销来说，以往的促销都是面向产品的促销，企业生产者很少从顾客角度考虑.现在企业销售产品都是面向顾客的促销，即生产的产品都经过严格调研且顾客需要的产品.这种观念的转变使得企业在制定目录时也应从顾客的角度出发，将顾客分成不同的顾客簇，并制定面向不同顾客群的目录，从而使目录对顾客簇产生最大效用.为使顾客对接收的目录感兴趣，要求每个顾客对接收的目录至少有兴趣度t.如此，目录分割问题变成了加入兴趣度约束的目录分割问题，也称面向顾客的目录分割问题.

1 目录分割问题

商业智能目录分割是基于单个企业效用的问题.设企业已对其顾客有充分了解，则可建立顾客数据库 (customers database)，用双向图G表示，G=(P，C，E)，P={p1，p2，…，pm}，C={c1，c2，…，cn}使用‖表示集合的基数，且其中，P是所有产品的集合;C是所有顾客的集合;E是边集，当且仅当顾客ci对产品pj感兴趣时，存在对应边eij，记做eij=(ci，pj).

1.1 目录分割定义

文献［3］已证明，基本分割问题是NP完全问题［3］.

定义2 顾客覆盖.若顾客对目录中至少1个产品感兴趣，则称该目录覆盖了此顾客.

下面给出目录分割问题的定义.用ω(P')［2］表示至少有1条边连接到产品集P'中的顶点c的顾客集合，即

定义3k目录分割问题［4］.用二分图G=(P，C，E)表示顾客数据库，且求P的k个子集P1，P2，…，Pk，和其对应C的k个子集C1，C2，…，Ck，使它们满足目标函数

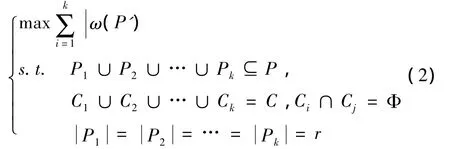
对于任意i和j，当i≠j时，Pi∩Pj可不必为空.

在定义3中，若将顾客分成k簇，每个顾客最多只能属于1个簇，每个簇对应的目录包含r个产品;而同一产品允许在多个产品簇中同时出现.

1.2 具有兴趣度约束的目录分割问题

定义1至定义3中的目录分割问题是以最大化覆盖顾客数量为目的.但实际上若顾客被目录所吸引，就会购买很多非目录产品.Ester等［2］引入最小兴趣度t，即在目录分割问题中加入兴趣度约束，使发送到顾客的产品目录至少有兴趣度t的顾客数量来测量顾客的整体效用.为形式化描述此问题，设 φ(P'，t)［2］表示至少有t条边连接到产品集P'中的顶点c的顾客集中，表达式为

2 最大顾客覆盖的目录分割算法

2.1 Naive算法

该算法提出解决目录分割问题的简单爬山算法［5］.首先依次选择支持度最高的前t个产品进入第1个目录;再计算此时覆盖的顾客;然后每次在目录中添加1个产品，要求是在未选产品中选择1个可覆盖增加顾客最多的产品，直到第1个目录含有r个产品结束;最后依次填充剩余目录.Naive算法虽然简单且易于实现，但实验效果差.

2.2 BPF算法

文献［6］提出解决顾客商品目录分割问题的BPF(best product fit)算法.根据对商品感兴趣的剩余顾客数量，和这些顾客需要感兴趣的当前商品目录中其他商品的数量，为每个商品赋予1个分值，从而提高已对目录中其他商品感兴趣的顾客所关注商品的优先权.图1给出了BPF算法描述.

图1 BPF算法描述 Fig.1 BPF algorithm

BPF算法的关键是确定商品P的评分函数，但它忽略了两个问题:①评分函数的两部分在函数中所起的作用不均衡;②第2部分未考虑对P的兴趣度，只考虑商品种类差异而忽视数量或利润的效用，导致聚簇性能下降，不能最大化全部顾客的效用f(x).

2.3 最大顾客覆盖目录分割算法的提出

为避免资源浪费，使用频繁模式树 (frequent-pattern tree，FP-tree)结构存储顾客数据库，即将顾客数据库映射到1棵树上，然后基于FP-tree设计相应的最大顾客覆盖的目录分割算法 (maximal customers cover for catalog segmentation，MCC-CS)，利用我们提出的基于兴趣度约束的目录分割算法，可将商品目录分割问题变成树深度搜索问题.

2.3.1 频繁模式树FP-tree结构定义

为找到能覆盖最多顾客的k个目录，需建立有效数据结构，同时存储事务和其对应的顾客信息.本研究使用树结构存储数据，即兴趣度t的约束.在构建树时仅构建顶上t层，顾客感兴趣的产品中支持度最高的t个产品就可覆盖其需求.将顾客对应的感兴趣产品按支持度降序排列，并取前t个插入树中.本研究使用改进后的FP-tree［6］结构存储数据，将每条交易对应的顾客信息存入对应的表中，称此树为t层兴趣度约束树 (frequent pattern tree witht-layer interest constraint).FP-tree每个树枝末尾加入顾客信息，如图2.

图2 频繁模式树示意Fig.2 FP-tree and its items lists

定义5 短交易.若顾客感兴趣的产品量小于t，则称该顾客交易为短交易.若将短交易插入树中，则叶节点到根的路径长度小于t，故没有必要将此交易插入树中.因此，在数据预处理中，可删除所有短交易和其对应的顾客信息.

定义6 锚节点［7］.它是距离FP-tree根节点t层的节点.若选择从锚节点到根上所有节点，则可覆盖全部顾客.FP-tree需维护2个表:频繁项列表按频繁计数降序排列;树下面的顾客表记录每个顾客对应的叶节点.

定义7 FP-tree.FP-tree是一种最高为t层的树结构，包含:①1个标记为null的根节点、1个项前缀子树作为根的孩子、1个频繁项表和1个顾客项表;②在项前缀子树上的每个节点包含项名称、频繁项和节点链3个域.其中，项名称记录当前项代表哪个节点;频繁项表示到此节点的频繁度，节点链链接到FP-tree上有相同名称的下一项，若无则为null;③在频繁项列表的每个入口包含项名称和节点链头2个域.其中，节点链头指向FP-tree上有相同项名称的第1个节点;④在顾客项表头的每个人包含顾客名称和节点链头2个域.其中，节点链头指向FP-tree上相应顾客交易的最后1个节点.

为构建FP-tree，需扫描数据库2次.第1次读取全部单个项，并将单个项按频繁度降序排列，构建FP-tree的根节点和链表;第2次扫描数据库，将事务数据库中的每个交易都插入FP-tree.

2.3.2 构建 FP-tree结构

基于上述定义构建FP-tree算法如下.

算法1.构建 FP-tree.算法输入为顾客数据库;输出为FP-tree.

①扫描数据库，找到所有频繁项集合和其对应的频繁度.将所有项按频繁度降序排列，所得链表记做Lf.

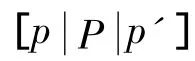
insert-tree(，T)操作.若T有同名项N，则将N计数加1;否则，创建新节点N，并将计数置1，将N的父节点链接到T，并将在频繁项表中对应的节点链头引出链接到此节点.若P∉Φ，则继续递归调用insert-tree(，T).

当插入操作完成后，在顾客项表中找到当前交易对应的顾客，并将其链接到p'上.

表1给出每个顾客感兴趣的产品示例数据库.设此时兴趣度t=3，修剪后的每条数据排在末列.

扫描表1数据库，删除短交易;按频繁度降序排列所有交易，并取前t个交易，得到项列表.然后扫描数据库构建相应的FP-tree，如图2(此处为清晰，将树上的节点到图2(a)相关的项上的链接省去).例如，对顾客C1，其对应的交易为I0，I1，I2，I4，将其排序为I0，I1，I2，由于t=3，则将其剪枝，仅保留前t个产品，即I0，I1，I2，然后将其插入FP-tree，成为最左边的树枝.对剩余的顾客交易，也使用类似方法插入.

表1 示例数据库Table 1 Example database

2.3.3 MCC-CS 算法

用FP-tree结构表示数据库，商品目录分割问题变成了在剪枝后的树上寻找某些节点的组合，并使该组合可最大限度地覆盖感兴趣的顾客.

算法2.MCC-CS算法.算法输入为历史交易记录Customer DB、目录数量k、每个目录包含的产品数量r及顾客兴趣度t;输出为k个目录和其对应的k个顾客簇.算法执行前需将每个顾客的所有交易合并为1条交易，删除所有短交易.按图3给出的MCC-CS算法描述，标记所有顾客为未覆盖顾客.

图3MCC-CS算法描述Fig.3 MCC-CS algorithm

MCC-CS算法在每次构建目录时需用未覆盖的顾客交易来构建1棵FP-tree，从而使构建的树能最大程度地覆盖尚未覆盖的顾客.

2.3.4 算法分析

MCC-CS算法为每个目录构建1棵FP-tree，共构建k棵树.构建1棵树，需扫描数据库2次.第1次获得所有未覆盖顾客对应商品的支持度，第2次将所有未覆盖顾客的交易插入树中，数据预处理完毕后，每个顾客仅对应1条交易.构建好树后，从树上选择节点进入当前目录需支持度最大的节点遍历当前树的r个节点.每个目录构建成功后，还要扫描数据库1次以便标记所有被当前目录覆盖的产品.因此，构建k个目录共需扫描3k次数据库.

3 实验及结果分析

为验证算法的有效性，我们在主频为2.66 GHz，内存为1 GB的PC上采用C++编程语言，对MCC-CS算法与BPF算法［6］性能进行比较.实验数据采集自CSDN-IT技术社区提供的IBM数据生产器［9］产生的合成数据库，含10×103个顾客，8×103个商品及50×103个交易.在数据预处理时合并了顾客交易，使得1个顾客仅对应1条交易，因此交易数量大减.为观测算法效果，同时采用BPF算法和Naive算法进行仿真对比.BPF算法是目前解决面向顾客的目录分割问题最佳算法.Naive算法指的是使用简单爬山算法得到的结果.

图4比较了最小兴趣度t变化时获得的目录覆盖的顾客数量.由图4可见，目录覆盖的顾客随着t的增加而减少.MCC-CS算法比BPF算法覆盖了更多的顾客.图5表示目录数量k变化影响的结果.目录覆盖的顾客量随着目录数量k增加而增加，符合市场规律.目录数量的增多表示对顾客进行了更多的细化，因而成本也要提高，获得的收益亦高.图6表示目录中产品数量r变化对结果的影响.当t=2，k=3时，目录所覆盖的顾客数量随产品量增加而增加.由图4至图6可见，MCC-CS算法获得了比其他算法更好的结果.这表明，MCC-CS算法能有效解决面向顾客的目录分割问题.

图4 顾客覆盖数随兴趣度的变化Fig.4 The number of customer cover by changes of interesting

图7是当k=3，r=80时目录覆盖的额外产品比较.额外产品指当前目录覆盖的顾客所购买的非目录产品.此时，BPF算法比MCC-CS算法覆盖了更多的额外产品，这是因为MCC-CS算法没有考虑此目标.BPF算法能覆盖较多额外产品，说明算法是松散的.MCC-CS算法所覆盖的额外产品更少，说明该算法产生的目录是紧密的.

图5 顾客覆盖数随目录数量的变化Fig.5 The number of customer cover by changes of catalog number

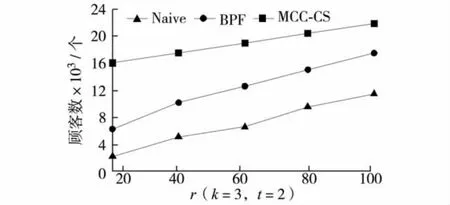
图6 顾客覆盖数随目录大小的变化Fig.6 The number of customer cover by changes of catalog size

图7 产品结果随兴趣度的变化Fig.7 The result of products by changes of interesting

结 语

本研究面向顾客的目录分割问题，提出基于FP-tree数据结构的MCC-CS算法.模拟测试结果表明.该算法使目录分割问题更具实用价值.下一步我们将加入利润约束，在为企业构建目录时兼顾利润条件，从而使构建的目录针对性更强，功效更好.

［1］Kleinberg J，Papadimitriou C，Raghavan P.数据挖掘微观经济思想 ［J］.数据挖掘与知识发现期刊，1998，2(4):311-324.(英文版)

［2］Ester M，GE Rong，JIN Wen，等.一种面向顾客目录分割的微观经济数据挖掘问题 ［C］//第10届ACM SIGKDD数据挖掘与知识发现国际会议论文集.西雅图:计算机协会，2004:557-562.(英文版)

［3］Kleinberg J，Papadimitriou C，Raghavan P.目录分割问题的近似算法［C］//第13届计算理论学术会议论文集.纽约:计算机协会，1998:321-219.(英文版)

［4］Kleinberg J，Papadimitriou C，Raghavan P.目录分割问题研究 ［J］.ACM 期刊，2004，51(2):263-280.(英文版)

［5］Charu C A.基于分割的流模型应用 ［C］//第9届SIAM数据挖掘国际会议论文集.斯帕克斯 (美国):工业和应用数学学会，2009:721-732.(英文版)

［6］HAN Jia-wei，PEI Jian，YIN Yi-wen.产生候选集频繁模式的数据挖掘［C］//ACM SIGMOD数据管理国际会议论文集.达拉斯(美国):计算机协会，2005，8(1):53-87.(英文版)

［7］HAN Jia-wei，WANG Jiang-yong，LU Ying，等.具有最小支持度的k层闭合频繁模式的数据挖掘 ［C］//第2届IEEE数据挖掘国际会议论文集.前桥 (日本):IEEE出版社.2002:211-218.(英文版)

［8］徐秀娟，王 喆，常晓宇，等.一种新的面向顾客的目录分割算法 ［J］.计算机研究与发展，2008，45(增刊1):310-315.

［9］Agrawal R.IBM同步数据发生器［M/OL］.［2004-09-23］ http://www.almaden.ibm.com/edquest/syndata.html.(英文版)

［10］Kleinberg J，Tardos E.算法设计 ［CP/DK］.阅读，新泽西 (美国):安德森·威斯利出版社，2005.(英文版)

［1］Kleinberg J，Papadimitriou C，Raghavan P.A microeconomie view of data mining［J］.Journal of Data Mining and Knowledge Discovery，1998，2(4):311-324.

［2］Ester M，GE Rong，JIN Wen，et a1.A microeconomic data mining problem:customer-oriented catalog segmentation［C］//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Seattle:Association for Computing Machinery，2004:557-562.

［3］Kleinberg J，Papadimitriou C，Raghavan P.Approximation algorithm for segmentation problems［C］//Proceedings of the 13th Annual ACM Symp on Theory of Computing.New York:Association for Computing Machinery，1998:321-219.

［4］Kleinberg J，Papadimitriou C，Raghavan P.Segmentation problems［J］.Journal of the ACM，2004，51(2):263-280.

［5］Charu C A.On seginent-based stream modeling and its application［C］//Proceedings of the 9th SIAM International Conference on Data Mining.Sparks(USA):Society for Industrial and Applied Mathematrs，2009:721-732.

［6］HAN Jia-wei，PEI Jian，YIN Yi-wen，et al.Mining frequent patterns without candidate generation:a frequent-Patterm tree approach［C］//Proceedings of the ACM SIGMOD Intemational Conference on Management of Data.Dallas(USA):Association for Computing Machinery，2000，8(1):53-87.

［7］HAN Jia-wei，WANG Jiang-yong，LU Ying，et al.Mining top-kfrequent closed patterns without minimum support［C］//Proceedings of the IEEE International Conference on DataMining. Maebashi(Japan):IEEE Press，2002:211-218.

［8］XU Xiu-juan，WANG Zhe，CHANG Xiao-yu，et al.A novel algorithm for the customer-oriented catalog segmentation problem ［J］.Journal of Computer Research and Development，2008，45(S1):310-315.(in Chinese)

［9］Agrawal R.IBM Synthetic Data Generator［M/OL］.［2004-09-23］ http://www.almaden/ibm.com/edquest/syndata.html.

［10］Kleinberg J，Tardos E.Algorithm Design ［CP/DK］.Reading.New Jersey:Addison-Wesley，2005.

A self-adaptive algorithm for the problem of catalog segmentation based on FP-tree†

LU Nan，DU Wen-feng，and LIANG Zheng-ping

College of Computer Science and Software Engineering Shenzhen University Shenzhen 518060 P.R.China

The customer-oriented catalog segmentation problem in the context of business intelligence was studied.Particularly，the catalog segmentation problem was casted as an optimization for maximizing the satisfaction of all customers subject to the requirement of at least t interestingness for each customer.To solve this problem，we introduced an improved frequent pattern tree to store the customer database and proposed a novel MCC-CS algorithm to optimize the selection of catalog products based on depth-first search strategy.Experimental results show that MCC-CS is capable of obtaining better performance than other state-of-the-art methods.

data mining;catalog segmentation;customer cover;frequent pattern tree;adaptive algorithm

TP 311

A

1000-2618(2011)04-0341-06

2010-12-14;

2011-04-10

广东省自然科学基金资助项目 (1015180600100)

陆 楠 (1959-)男 (汉族)，上海市人，深圳大学教授、博士.E-mail:lunan@szu.edu.cn

Abstract:1000-2618(2011)04-0346-EA

† This work was supported by the Natural Science Foundation of Guangdong Province(1015180600100).

【中文责编:英 子;英文责编:雨 辰】