网络控制系统的时延估算及补偿

温阳东，李 彧

(合肥工业大学 电气与自动化工程学院，安徽 合肥 230009)

在网络控制系统中，传感器、控制器和执行器通过网络交换数据时，由于带宽和数据流量变化不规则等原因，会出现网络拥塞等现象，导致节点与节点间的信息交换出现时间延迟。这种由于网络介入而使控制系统的信息传输产生的时延，称为网络时延。网络时延的产生使得系统控制品质降低，甚至导致系统的不稳定。

网络时延由几个部分组成[1]：(1)传感器节点采集数据以及处理数据所需要的时间。(2)传感器节点竞争发送权等待的时间和传感器数据在网络中的传输时间。(3)控制器节点计算控制量、处理数据所需要的时间。(4)控制器节点竞争发送权等待的时间和控制量在网络中的传输时间。(5)执行器节点处理数据所需要的时间。通常，为研究方便，将设备时延和通信时延合并考虑，即传感器到控制器时延τksc和控制器到执行器时延τkca。则网络控制系统的时延为 τk=τksc+τkca。

1 时延的计算方法

网络控制系统由于时延的存在，会给系统的稳定性带来影响。预估控制可以对网络系统的时延进行预先计算，然后对下一步控制做出修正以补偿时延所带来的影响。

假设传感器采用时间驱动，控制器与执行器采用事件驱动。则G(s)为不包含纯滞后的被控对象的传递函数，C(s)为控制器，D(s)为干扰信号。如图1所示。系统传递函数为：

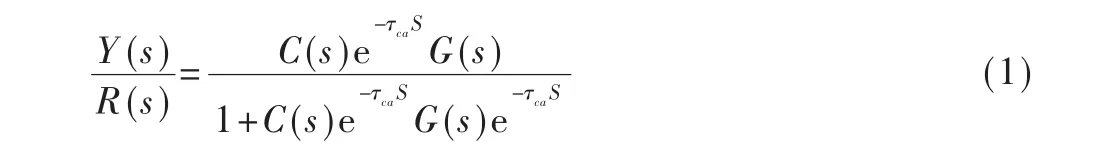
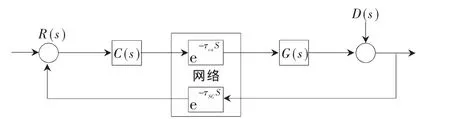
图1 网络控制系统结构

有多种方法可估算出 τksc和 τkca值，例如往返时延动态估计法、平均窗口法[2]、均值法等。本文采用时间戳法对时延进行估计[3]。所谓时间戳法就是将数据产生的时间和数据一起发送出去。在网络间传输的数据包中既有数据信息，也有时间信息。在网络控制系统中，传感器把测量值及其时间放在一个数据包中，使得控制器在收到测量值的同时也得到了时间戳，并将该时戳值与本地时钟比较，很容易计算出时延值。

把不同节点的时间换算到同一个节点进行计算。具体方法如下：系统中A、B两个节点，设ti为基准时间(绝对时间)，tAi为 A点的本地时间，tBi为 B点的本地时间，有下面的公式：

其中 αA和 αB为时间误差，设时钟误差为 Δ，那么

由式(1)、式(2)可以得到：

节点A在t1A时发送读请求信号，节点B在接收到信号后在t2B时返回信号，并且返回信号在t3A时到达节点A。那么TAB是从节点A到节点B信号的传送时间，即为时延。

对于时钟误差Δ，可以通过多次计算取平均值得出：

可以用时间戳法较为容易地计算出 τksc。 对于 τkca，同样可以用时间戳法算出。但是由于控制器节点计算控制命令时还不能得到实时的τkca，因此可以用平均值E{τkca}代替 τkca。 那么，τksc+E{τkca}就是从传感器节点发出信号到执行器节点采用控制信号整个过程的总时延。

使用时间戳法最关键的是要保证各节点的时钟同步。在许多技术型系统中，对时钟同步的要求越来越高。目前，存在多种网络系统的时钟同步协议，例如：DTP(Day Time Protocol)，TP(Time Protocol)，NTP(Network Time Protocol)[4]。但是，许多控制应用要求比较高精度的时钟同步，以上几种协议精度均不高。IEE1588精确时间协议的时钟同步精度最高可达亚微秒级。现简单介绍PTP(Precision Time Protocol)的 基 本 原 理[5]。

PTP基本原理是在各个节点之间传递和交换同步报文，通过主从时钟的时钟偏差和报文传输时延来修正本地时钟。主时钟根据一定的时间周期发送同步信息，紧接着发送Follow_up信息，该信息中包含同步信息的准确发送时间T1，从时钟记录下同步信息的到达时间T2，紧接着在T3时刻发送Delay_Req信息，主时钟记录Delay_Req信息的到达时间T4，并发送Delay_Resp信息把T4告诉从时钟。从时钟根据4个时间信息计算出两个时钟的偏差和传输时延，以此来修正从时钟，最终使其与主时钟同步。

2 时延补偿

由于时延会给系统的稳定性和控制指标带来一系列影响，可以使用预估控制算法对系统进行修正，补偿时延带来的影响。比较流行的算法有预估模型算法控制、广义预测控制[6]、内模控制[7]等。本文运用 Smith补偿算法，将Smith预估器加入网络控制系统中[8]。

从式(1)可以看出，分母中出现了指数项，这就会降低系统的稳定性，甚至导致系统不稳定。为此，在控制端加入Smith预估器。如图2所示。

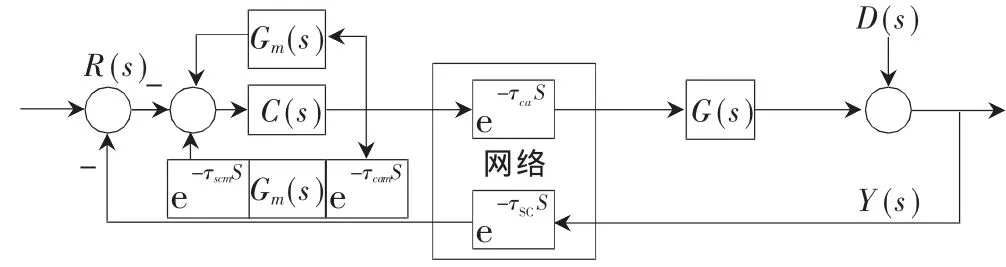
图2 基于Smith预估器的网络控制系统

系统的闭环传递函数为：

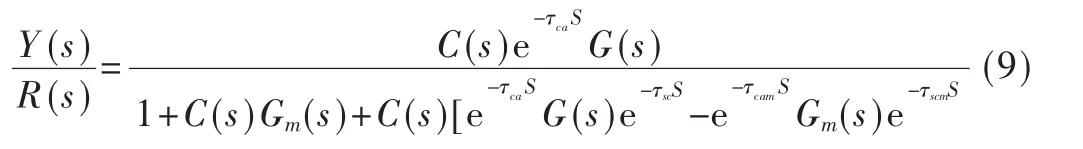
式 中 ，Gm(s)是 G(s)的 预 估 模 型 ，e-τcamS和 e-τscaS分 别 是e-τcaS和 e-τscS的 预 估模型。 当 τcam=τca，τscm=τsc，Gm(s)=G(s)即预估模型等于实际模型，传递函数变为：

从式(10)中可以看出，分母中不含有指数项，从而实现了对网络时延的完全补偿。将Smith预估器运用到网络控制系统，关键是对时延做出比较准确的预估，即预估出τscm和τcam。通过时间戳法可以比较准确的估算出τscm和τcam。

3 仿真

对带有Smith预估器的网络控制系统进行仿真，以此来观察时延补偿后系统的响应。采用常规的PI控制，其中KP=30，Kl=30。 Smith 预估模型 Gm(s)e-τscmS为：

在系统中加入随机干扰和不加随机干扰，仿真结果如图 3、图 4和图5所示。

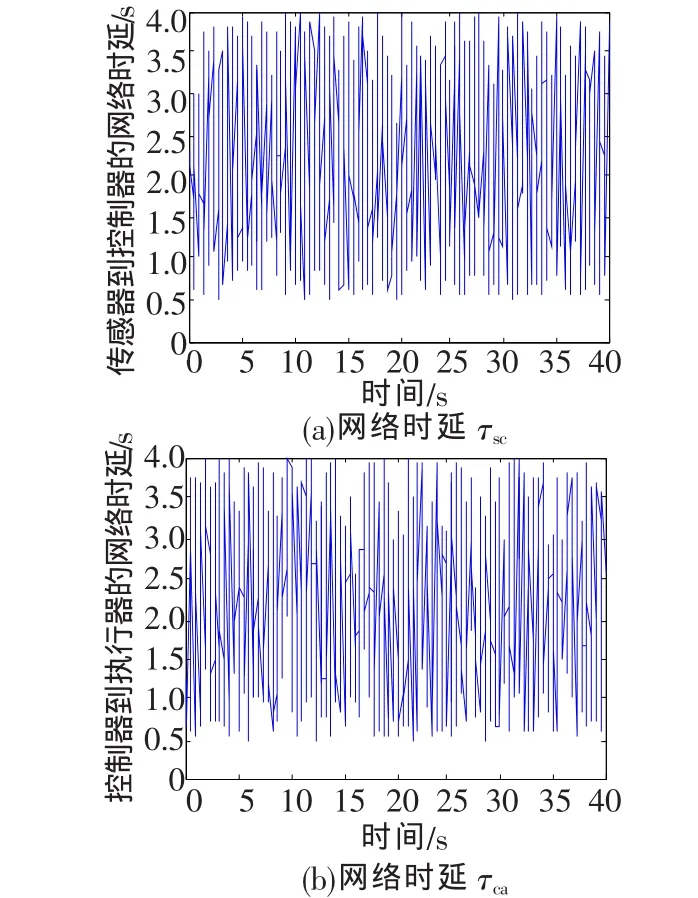
图3 网络时延

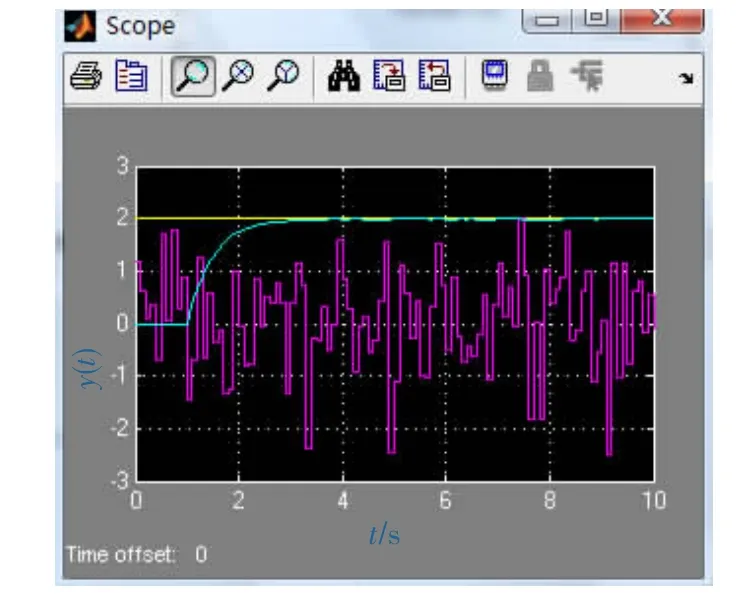
图4 史密斯预估控制仿真图(有随机干扰)

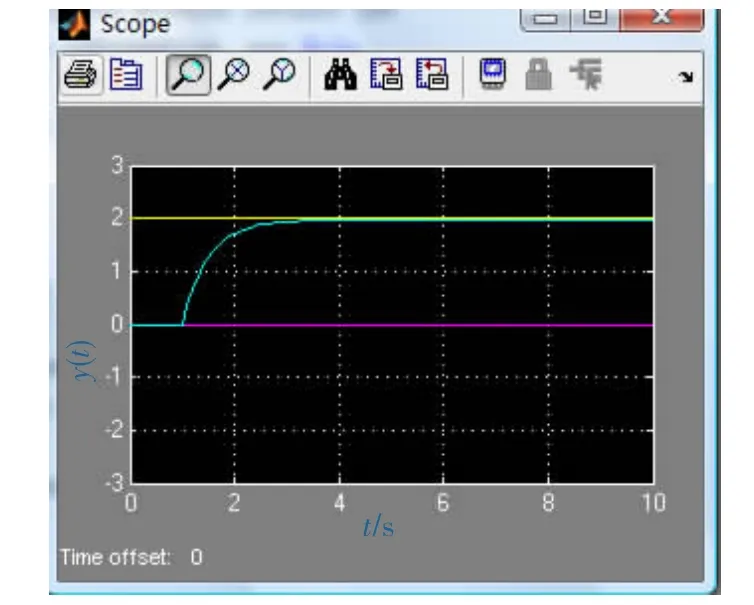
图5 史密斯预估控制仿真图(无随机干扰)

从仿真图中看出，在网络环境下加入史密斯预估器，对时延进行补偿，无论系统里是否有随机干扰，都可使输出响应较为稳定。

在网络控制系统中，时延的存在会降低控制的品质，甚至会使系统瘫痪。本文将时间戳法和Smith预估补偿法结合起来，运用时间戳法来估算时延。通过仿真，得到的响应较为稳定。由此，只要采用适合的网络时延动态补偿器，并对网络进行补偿，网络控制系统是可以实现稳定的。

[1]王岩，孙增圻.网络控制系统分析与设计[M].北京：清华大学出版社，2009：48-52.

[2]周洪，邓其军，孟红霞，等.网络控制技术及应用[M].北京：中国电力出版社，2007：100-106.

[3]Hua Jiwei， Liang Tao， Lei Zhaoming.Design time-stamp based state prediction controller for networked control systems[C].Wirless Communication，Networking and Mobile Computing，2008.WiCOM’08 4thInternational Conference，2008：1-4.

[4]MILLS D L.Internet time synchronization：The network time protocol[C].IEEE Transactions on Communications，1991.

[5]王相周，陈华婵.IEEE精确时间协议的研究与应用[J].计算机工程与设计，2009：1846-1849.

[6]李彬.网络控制系统时延分析与补偿[D].西安：西安工业大学，2006.

[7]鲁照权，韩江洪.一类大时滞过程的内模预测控制[J].合肥工业大学学报(自然科学版)，2001，24(1)：1-5.

[8]杜峰，钱清泉，杜文才.基于新型 Smith预估器的网络控制系统[J].西南交通大学学报，2010，45(1)，65-69.