基于三次样条函数的数控插补算法研究

孙旭霞，张 英

(西安理工大学 自动化与信息工程学院，陕西 西安710048)

随着微电子技术、计算机技术、自动控制技术和通信技术的不断进步，现代数控系统的发展趋向高性能化。其中性能的完善主要体现在高速度、高精度、高可靠性、多功能化、网络化、小型化、多样化、智能化和开放性等方面。插补技术是数控系统的核心，为使高档数控系统能发挥其功能，高精度、高速度、高效率的插补算法成为目前研究需要突破的难点[1]。

在数控插补装置上，针对船身外放样时的样条曲线，汽车、飞机及各种产品的外形曲线等无法用标准代数方程描述的复杂曲线，一般都采用直线逼近或圆弧逼近的方法来实现其插补，然而这种方法所编写的算法较为复杂，且在计算过程中还会产生计算误差及误差的累积，降低了插补的精度。而三次样条函数基于可使曲线各分段处保持一定程度的光滑性，其具有很好的保凸性和光顺性，且能保持曲线的连续性。同时三次样条函数的应用范围广泛，特别是在给定型值点的曲线拟合方面，如在插补装置中实现凸轮、汽车外轮廓等曲线。因此对于某些复杂零件，采用三次样条函数的插补方法描述其轮廓是一种极为有效的手段。基于三次样条函数的上述特性，本文描述了三次样条曲线形成曲线轮廓并在数控插补装置上实现插补的过程。该方法既能提高插补精度，又使计算不太复 杂[2，3]。

1 三次样条函数的定义

三次样条函数的定义如下：设有n个离散点，分别为 p1(x1，y1)、p2(x2，y2)、…、pn(xn，yn),且 x1＜x2＜…＜xn，若曲线 S(x)满足以下几个条件则称 S(x)为区间[x1，xn]上以xj(j=1，2，…，n)为型值的三次样条函数。

（1）S(x)通过所有型值点，且 S(xj)=yj(j=1，2，…，n)；

（2）S(x)在区间[x1,xn]内，存在连续的一阶导数、二阶导数；

（3）S(x)在 每 个 子 区 间[xj，xj+1]内 ， 均 可 采 用 三 次 多项式来表示，即 Sj(x)=aj+bj(x-xj)+cj(x-xj)2+dj(x-xj)3，(j=1，2，…，n-1)。

下文将利用型值点处二阶导数相等的边界条件来求得三次样条函数，并给出具体的推导过程。

2 三次样条曲线轮廓的拟合原理

利用三次样条函数解决复杂曲线插补问题的思路是：在被插补的复杂曲线上找到一定数量的型值点，采用三次样条求出插补中间点，然后利用相邻两端曲线交点处的一阶导数、二阶导数相等这一条件，实现整段曲线连续且在曲线连接处平滑过渡的效果。

首先构造满足条件的三次样条函数S(x)的表达式。假定 S′j(x)=mj(j=1，2，…，n)，则由分段三次埃尔米特插值公式[4]可得：

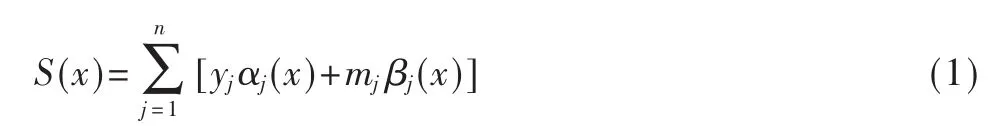
其中 αj(x)、βj(x)是插值基函数。 显然，表达式中 S(x)及S′(x)在 整 个 区 间[a，b]上 连 续 ，且 满 足 S(xj)=yj(j=1，2，…，n)，只要求得mj，三次样条函数就可以构造成功。下面是mj的求解过程。

利用插值基函数需满足的条件求出 αj(x)、βj(x)，即可得出 S(x)在[xj，xj+1]上的表达式为：

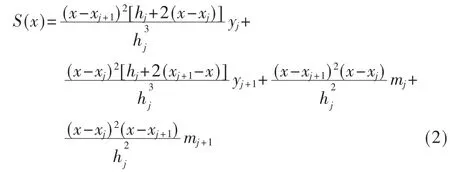
其中 hj=xj+1-xj。 对 S(x)在[xj，xj+1]上求二次导数得：

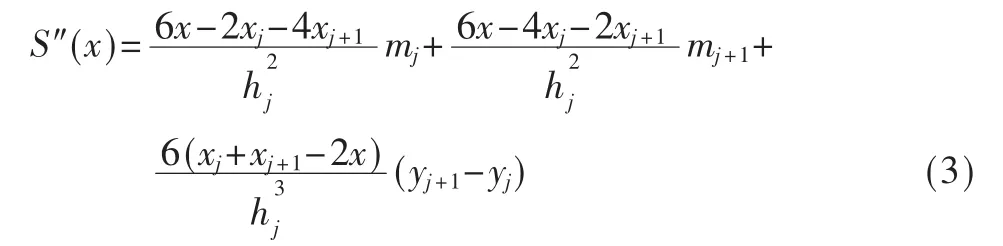
由式(3)可推导出：

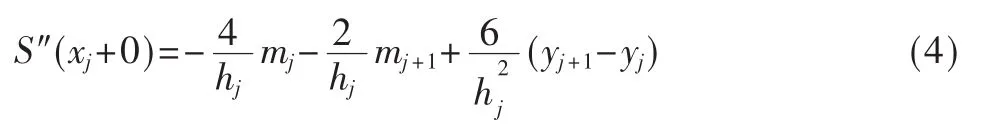
同理可得 S″(x)在区间[xj-1，xj]的表达式为：

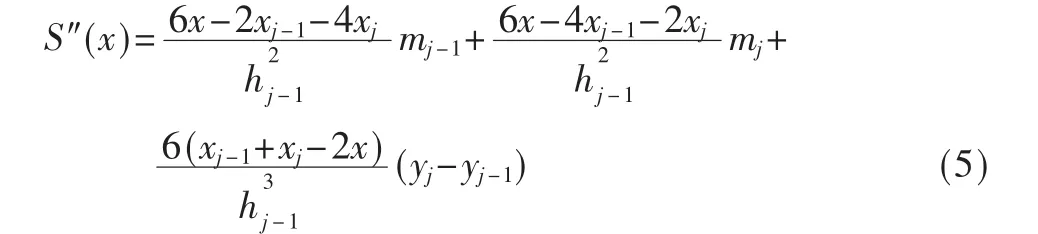
则：

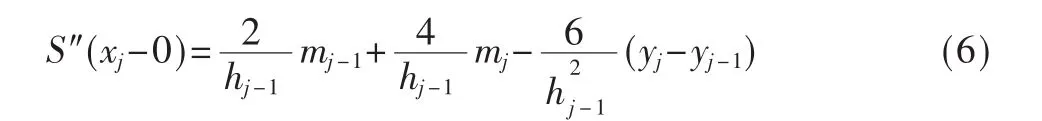
由条件 S″(xj+0)=S″(xj-0)(j=2，3，…，n-1)，可得：

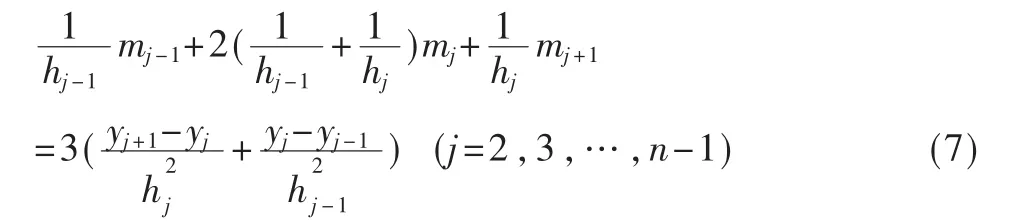
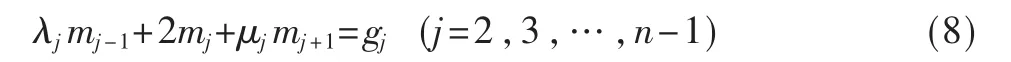
其中：

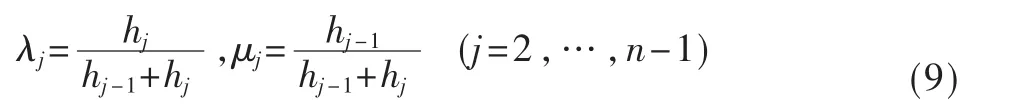
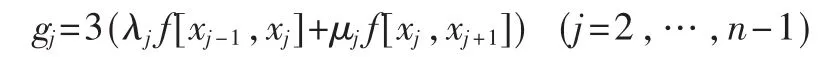
若边界条件为 S″(x1)=S″(xn)=0，即满足自然边界条件[3，5]，则得两端的方 程为：

式(8)、式(10)用矩阵形式表示为 Am=g，即：

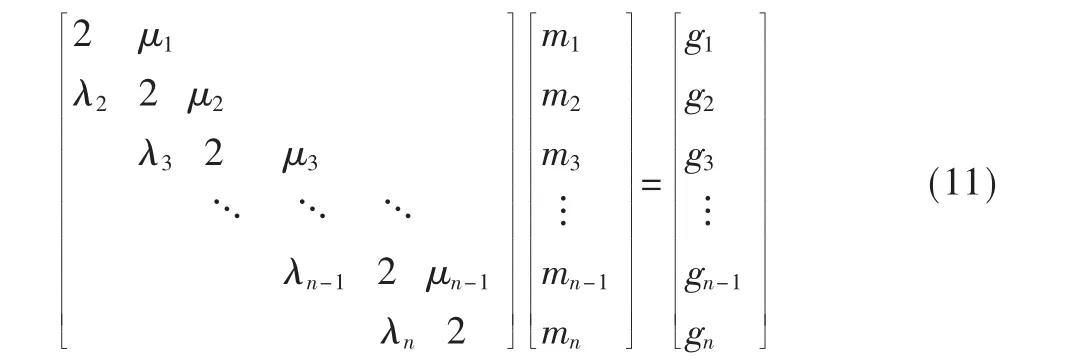
将上式中的A分解为下三角矩阵L及单位上三角矩阵U的乘积，即A=LU，其中 L、U如式(12)所示。

利用矩阵乘法公式及追赶法求得mj(j=1，…，n)。

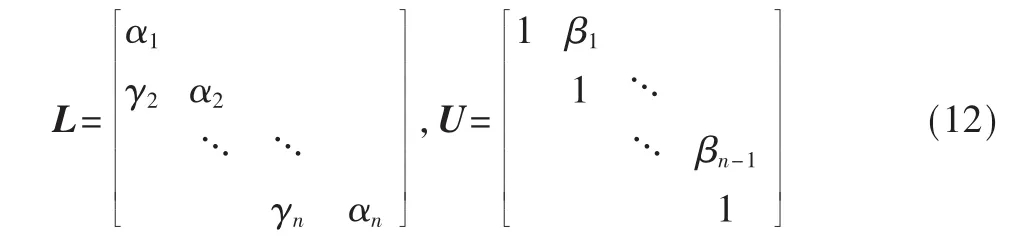
最终由式(2)计算出 S(x)。

3 基于三次样条函数的插补算法

根据以上的拟合原理，结合插补算法原理，可以生成基于三次样条函数的插补算法，步骤如下：

（1）根据曲线选出 n个型值点，其坐标值为(xj，yj)，(j=1，2，…，n)，并使得 x1＜x2…＜xn。

（2）求 mj(j=1，…，n)的值。

令 hj=xj+1-xj；μj=hj-1/(hj-1+hj)；

λj=hj/(hj-1+hj)；mj=yj′；

求得：

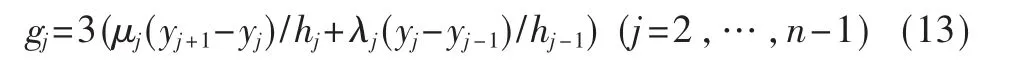
取 μ1=1，λn=1；

得：g1=3(y2-y1)/h1，gn=3(yn-yn-1)/hn-1；

利用矩阵乘法公式[6-8]得：

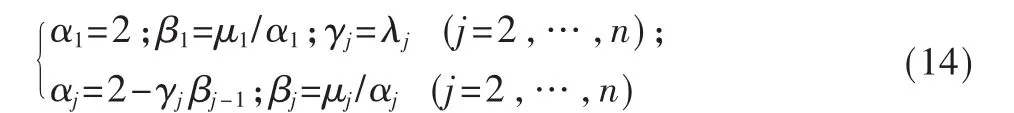
利用追赶法根据LR=g得：

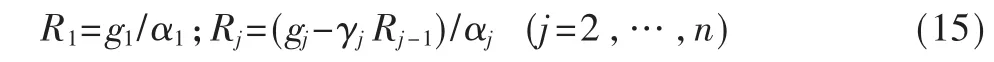
由Um=R得：

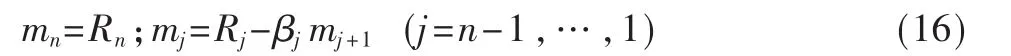
（3）求三次样条函数的系数。经过上面一系列的计算之后，可得该函数的系数如下：

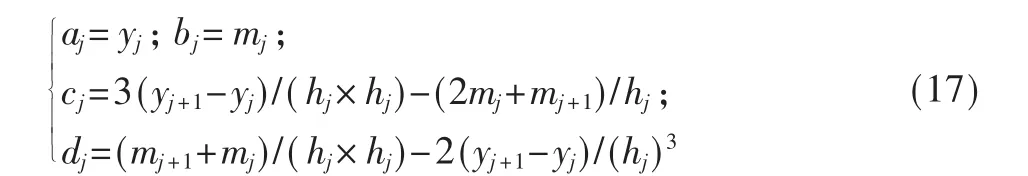
（4）求三次样条函数的表达式。将式(17)代入式(18)中即可得出三次样条函数的表达式：

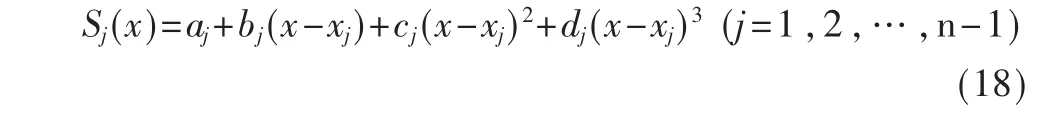
以[xj，xj+1]为例，该算法的插补过程如下：此为三次样条曲线中第j段的插补，x轴以xj为起点坐标，x每次累加△x，再根据函数表达式计算出Sj(x)的值，照此循环计算，就可算出每一段函数每一点x所对应的函数值，最终得到插补点X、Y轴的坐标值，并输出每一点的坐标值，直到x=xj+1，整段的插补即完成了。其中△x为正整数，且其所取值必须使得（xj+1-xj）/△x为整数，并确保Y坐标值的变化量大于1。其他段按上述原理继续进行相应的插补计算。

4 在数控装置上的实现

4.1 数控装置的介绍

本文使用以S3C2410为主芯片的ARM开发板作为数控装置。ARM采用RISC结构，能在一个机器周期内执行一条指令。此开发板属于ARM9处理器系列，具有ICache和DCache，提高了存储器访问的效率，具有64 MB NAND Flash和64 MB SDRAM的储存容量。其晶振频率为12 MHz，而时钟控制逻辑能够产生4倍晶振频率的PCLK时钟信号，即为48 MHz。用该PCLK值计算所得的定时器输入频率高，从而使得定时时间能设定得很短。以上特性使此插补算法能在该装置上得以运行，且具有较高的插补速度，以实现三次样条曲线的插补。

在ARM开发板上外接两个步进电机，分别用于实现X轴和Y轴方向的插补。通过改变定时计数器的初值，使得脉冲输出速度不同，从而实现步进电机以不同速度沿X轴和Y轴运行。

三次样条曲线的插补算法流程如图1所示。

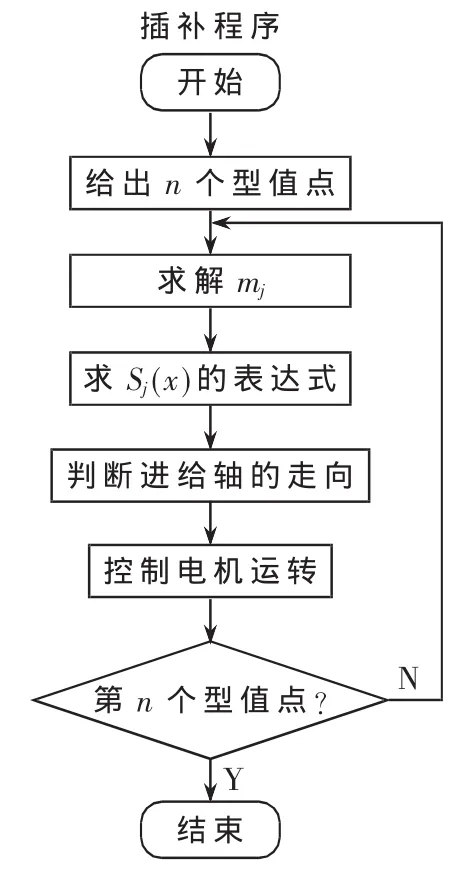
图1 插补算法的流程

4.2 实验结果及分析

为了验证三次样条函数插补方法的可行性，取一组满足三次样条函数的型值点，根据三次样条函数的拟合原理编程，拟合出如图2所示的三次样条曲线。

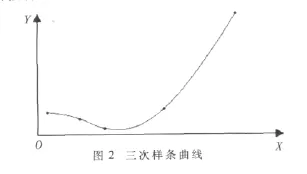
图2是整个三次样条曲线的轮廓，为了把这种方法应用在数控插补上，还必须在此基础上取适当的插补点，在ADS1.2集成环境下，用ARM开发板进行调试，在此装置上运行之后，使得步进电机依插补结果运转，运行结果如图3所示。

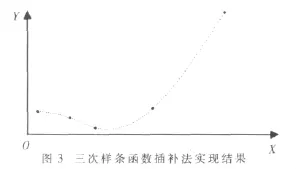
按照以上两图的实现结果进行如下分析：图2是按照拟合原理拟合出来的完整三次样条曲线的轮廓，该曲线相邻两端交点处一阶导数、二阶导数相等，具有很好的光顺性，且保持良好的连续性。图3是在三次样条曲线基础上取适当的插补点进行插补的结果，取的插补点越密集，插补结果就越接近真实曲线，精度也就越高。由插补算法可知Y坐标值是根据X坐标值计算所得，最终求得y的变化量，因此x所对应的I/O每输出一个脉冲，y对应的I/O输出的脉冲数根据计算结果而变化。由于插补的每个点都确保在此三次样条曲线上，比起用直线或圆弧逼近曲线的方法，插补效果在准确度和精确度上明显提高。

在数控装置上，利用三次样条函数不仅能够进行简单曲线的插补计算，对于无法通过直线、圆弧以及其他二次曲线来描述其轮廓的复杂零件，同样能实现其插补，同时具有很好的保凸性和光顺性，且保证了插值函数的连续性及插补的精度，增加了数控装置的曲线应用范围。本文以ARM开发板作为数控装置，对此插补算法进行了验证，该方法算法简单，易实现，精度较高，插补效果好。

[1]卢胜利，王睿鹏，祝玲.现代数控系统—原理、构成与实例[M].北京：机械工业出版社，2007.

[2]包园园.三次样条函数在自由曲线测量中的应用研究[J].机械制造与自动化，2009，38(2)：88-89.

[3]王茹传，黄海平，林巧民.计算机图形学（第 2版）[M].北京：人民邮电出版社，2009.

[4]聂玉峰.Lagrange插值和Hermite插值的内在统一理论[J].高等数学研究，2010，13(1)：13-14.

[5]邹淑芳.三次样条函数的基样条法和三弯矩法之异同比较[J].云南电大学报，2009，11(2)：93-96.

[6]Sun Ningping，AYABE T，NISHIZAKI T.Efficient spline interpolation curve modeling[C].Intelligent Information Hiding and Multimedia Signal Processing，2007：59-62.

[7]许小勇，钟太勇.三次样条插值函数的构造与Matlab实现[J].自动测量与控制，2006，25(11)：76-78.

[8]孙令德.计算机图形学实践教程（Visual C++版）[M].北京：清华大学出版社，2008.