一种空域和频域相结合的运动图像亚像素配准技术

孙 辉，李志强，孙丽娜，郎小龙

（中国科学院长春光学精密机械与物理研究所，吉林长春130033）

一种空域和频域相结合的运动图像亚像素配准技术

孙 辉，李志强，孙丽娜，郎小龙

（中国科学院长春光学精密机械与物理研究所，吉林长春130033）

针对视频图像运动检测问题，提出了一种结合空域灰度投影和频域相位相关的亚像素图像配准方法。首先，采用灰度投影算法在空域对运动图像进行粗配准，即在图像行和列方向上计算图像灰度投影特征数据，根据灰度相关函数最小化准则，估计像素级运动量；然后，在经过粗配准的两幅图像中心选取尺寸相同的区域，进行快速傅里叶变换，在频域采用扩展的相位相关算法对图像进行精确配准。该方法利用图像的功率谱信息，减少对图像内容的依赖，运用基于最小二乘的曲面拟合法，实现亚像素图像配准参数估计，具有从粗到精的特点，有效提高了图像检测精度。文中最后对样本图像进行了图像配准对比实验，结果表明，该方法可以检测0.01 pixel的运动量，最大配准误差为0.004 8 pixel。

灰度投影；相位相关；图像配准；亚像素；运动检测

1 引 言

图像配准是对来自不同场景、不同视点、不同传感器或不同时间的两幅或多幅图像进行对准的过程。近年来，随着视频技术、数字图像技术的广泛应用，图像配准技术受到了广大专家学者的高度重视，并在遥感图像［1］、航空影像［2］、医学影像［3～5］、运动检测［6～8］等方面得到广泛的应用，目前已成为计算机视觉研究领域发展迅速的图像处理技术之一。

图像配准算法有很多，如：基于插值法、扩展的相位相关法、解最优化问题法等［9］。按配准精度划分，图像配准可分为像素级和亚像素级。典型的像素级配准技术包括图像匹配、灰度投影算法、梯度法［10］等，其优点是算法简单，易于硬件实现，缺点是配准精度较低，仅能检测像素级或更低的精度。亚像素级配准技术包括扩展的相位相关法［11］、插值法［12］等，文献［11］对基于傅里叶变换的相位相关法［13］进行了改进，提出了一种扩展的相位相关算法，通过计算两幅图像的相位相关函数，实现图像的精确配准，精度可达1/100 pixel。虽然相位相关法在配准精度上有明显优势，但由于采用了频域相关技术，当待配准的两幅图像确实相关时，相关函数存在一个尖锐的峰值，可以实现图像的精确配准；而当两幅图像相关程度较差时，相关函数没有尖锐的峰值特征，配准误差较大。在视频图像序列中，由于两幅图像之间的相对位移，其相关程度会随着位移量的增大而减小，在这种情况下，直接使用扩展的相位相关法会带来较大的配准误差，直接影响运动检测结果。

本文针对序列图像的运动检测问题，提出一种在空域上的灰度投影算法和频域上的相位相关算法相结合的配准方法，即首先在空域使用灰度投影算法检测像素级的运动量，根据检测结果粗略配准两幅待配准的图像。然后在两幅图像中心选取相同尺寸的区域并进行傅里叶变换，在频域进行相位相关运算，进而实现运动图像亚像素级的精确配准。本文方法具有从粗到精的特点，实现了空域和频域算法的优势互补，有效提高了图像检测精度和效率。

2 二维平移运动模型

根据载体运动的复杂性不同，描述图像二维运动模型通常包括平移、旋转、比例缩放及仿射变换等，其中最简单同时也是最常用的是在x和y轴方向的平移运动。

二维平移运动模型是一种线性变换，可以表示为：

式中，（Xc，Yc），（Xr，Yr）分别表示位移图像和参考图像像素点坐标，dx，dy表示位移图像相对参考图像的运动量，用来描述图像在水平和垂直方向上的瞬时运动。图像位移矢量定义为：

根据平移运动模型，本文通过灰度投影算法和相位相关算法相结合的平移运动复合配准方法估计两幅图像之间的位移矢量V，配准精度可实现亚像素，配准流程如图1所示。

图1 亚像素配准流程Fig.1 Basic flow chart for sub-pixel registration

3 亚像素图像配准

3.1 空域灰度投影技术：图像粗配准

灰度投影算法（Gray Projection Algorithm，GPA）是一种空域特征相关技术，其基本思想是将一幅M×N图像的二维灰度信息｛f（x，y）}映射成两个独立的一维投影序列｛X（x）}和｛Y（y）}作为特征数据，通过两幅图像X（x）和Y（y）的相关计算估计位移量。灰度投影数据计算公式如下：

式中，Xκ（x），Yκ（y）分别表示第κ帧图像｛fκ（x，y）}的第x列和第y行的灰度投影值。

图2显示了一幅原始图像（Milkdrop）及其在行和列方向上的归一化的灰度投影曲线。

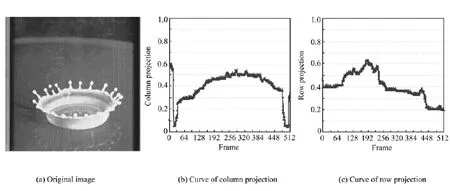
图2 原始图像及其投影曲线Fig.2 Original image and its gray projection curves

将行和列方向上的投影数据作为特征，对参考图像和位移图像做互相关运算，参考图像可以是运动过程中某一时刻的图像，也可以是前一幅图像。根据最佳匹配准则，采用全局搜索算法，即对搜索宽度范围内的所有点进行一次相关运算，根据相关曲线的峰值确定位移图像相对参考图像的运动量。

本文采用最小均方误差（MSE）作为最佳匹配准则，构造相关函数如下：

式中（p，q）∈A，A表示全部投影矢量的集合。

根据上述定义，运动矢量估计变成在（p，q）∈A范围内，求R（p，q）的最小值问题。即：

得到了水平和垂直方向的运动量后，将位移图像向位移矢量相反的方向移动，就可以粗略地补偿图像之间的运动，实现像素级的粗配准，并为进一步精确配准做准备。

灰度投影算法具有下述显著特点：

（1）算法简单，运算量小；

（2）对噪声干扰不敏感；

（3）配准精度低，只有一个像素或更低。

3.2 频域相位相关技术：图像精确配准

相位相关配准算法（Phase Correlation Algorithm，PCA）是一种非线性、基于傅里叶功率谱的频域相关技术，由于该方法只取互功率谱中的相位信息，对噪声有较好的容忍度，同时减少了对图像内容的依赖，具有较好的鲁棒性。

设f1（x，y）和f2（x，y）是经过上述粗配准后的两幅图像，目的是精确地估计 f2（x，y）相对于f1（x，y）的亚像素级平移运动矢量V0=［x0，y0］T。根据图像运动模型，f2（x，y）和f1（x，y）满足如下关系：

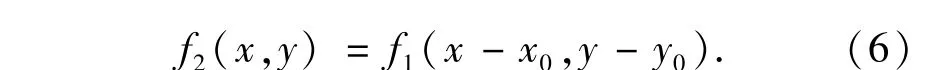
设F1（u，υ）和F2（u，υ）分别表示f1（x，y）和f2（x，y）的傅里叶变换，则有：

两幅图像之间归一化的互功率谱可表示为：

将式（8）两端进行傅里叶逆变换，可得相位相关函数的表达式如下：

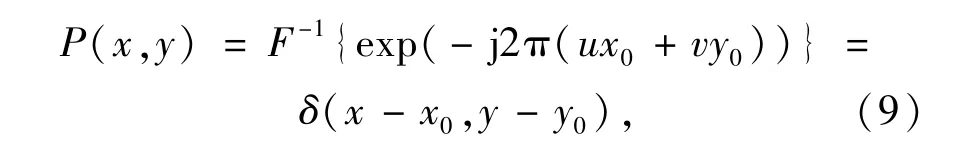
式（9）中：δ（x-x0，y-y0）为典型的Dirachlet函数，该函数在中心点（x0，y0）处不为零，在其它位置都是零，相关函数的峰值幅度反映了两幅图像匹配程度，理想状态下，相关函数峰值为1。

图3显示了相位相关函数曲线图，可以看出，随着位移量的增加，相关函数曲线的尖峰越来越小。

图3 相位相关函数p（x，y）的3D图Fig.3 3D plots of phase correlation function p（x，y）

为获取亚像素级运动量，采用基于最小二乘的二次曲面拟合方法，即通过在相关峰值坐标点附近用曲面拟合相位相关值，拟合曲面的峰值坐标即为位移矢量V0=［x0，y0］T。

4 实验结果

4.1 样本图像

样本图像选用标准样本图像库中的lake图像，图像分辨率为512×512×8 bit，原始图像作为参考图像，如图4（a）所示，位移图像通过对原始图像平移得到，不失一般性，本文只对原始图像进行水平方向的平移运动，即步长为0.5 pixel的平移操作，一共生成30幅对比图像，其中第15帧位移dx=7.5 pixel，第30帧位移dx=15 pixel，如图4（b）、图4（c）所示。位移图像的亚像素位移曲线见图5。

图4 样本图像Fig.4 Sampling images

图5 亚像素位移曲线Fig.5 Curve of sub-pixel displacement

4.2 图像配准实验

首先直接采用频域相位相关配准算法对样本图像进行位移量检测，计算从第1帧到第30帧位移图像的亚像素级位移量。为客观描述位移量的检测能力，本文将检测结果位移量与真实位移量的差值作为配准误差，即：

配准误差=检测位移量-真实位移量

由于每幅位移图像相对原始图像的真实位移量已知，可以统计配准结果与真实位移量的误差。频域相位相关配准结果及配准误差统计结果分别如图6（a）、图6（b）所示，样本配准最大误差为17.014 pixel，误差均方值RMSE=5.79 pixel。

图6 相位相关配准结果及误差曲线Fig.6 Experimental curves of registration with PCA

根据前文分析，当两幅图像相关程度较差时，相位相关算法效果较差。从图中的配准结果和配准误差曲线也可以看出，在第18幅图像以后（图像位移量超过8 pixel）时，配准误差越来越大。

采用本文提出的空域灰度投影算法与频域相位相关算法相结合的方法进行配准对比实验，配准位移结果及配准误差统计结果分别如图7（a）、图7（b）所示。配准结果显示：在30个样本图像中，配准误差最大值为0.004 8 pixel，误差均方值RMSE=0.001 2 pixel。从配准结果可以看出，该方法具有较高的配准精度。

图7 本文方法配准结果及误差曲线Fig.7 Experimental curves of registration with GPA and PCA

5 结 论

域采用相位相关算法进行精确配准，得到高精度的位移参数。

实验结果表明，本文方法克服了灰度投影算法在配准精度方面的不足，同时解决了直接使用相位相关配准算法不能处理较大运动量的问题，充分发挥了两种算法的优势，有效提高了图像检测精度和效率。由于灰度投影算法的特征数据来自图像的灰度统计数据，相位相关算法利用了图像的互功率谱信息，两种算法都减少了对图像内容的依赖，所以本文方法具有较强的抗噪能力，有较好的鲁棒性和可行性。

本文针对视频图像运动检测问题，提出了一种结合空域灰度投影算法和频域相位相关的图像配准方法，并将该方法应用于视频序列图像的亚像素运动检测。介绍了灰度投影算法和相位相关配准方法的特点，分析了两种算法在检测图像位移量方面的能力。首先采用灰度投影算法检测两幅图像之间的运动量，对图像进行粗配准。然后对经过粗配准的两幅图像进行傅里叶变换，在频

［1］强赞霞，彭嘉雄，王洪群.基于傅里叶变换的遥感图像配准方法［J］.红外与激光工程，2004，33（4）：385-387.QIANG Z X，PENG J X，WANG H Q.Remote sensing image registration algorithm based on FFT［J］.Infrared and Laser Eng.，2004，33（4）：385-387.（in Chinese）

［2］王志强，程红，孙文邦，等.基于改进Harris算法的航空影像自动配准算法［J］.遥感信息，2008，（6）：18-21.WANG ZH Q，CHENG H，SUN W B，et al..Automatic registration algorithm of aerophotos based on improved harris operator［J］.Remote Sensing Information，2008，（6）：18-21.（in Chinese）

［3］冯林，管慧娟、藤弘飞.基于互信息的医学图像配准技术研究进展［J］.生物医学工程学，2005，22（5）：1078-1081.FENG L，GUAN H J，TENG H F.Advances in medical image registration based on mutual information［J］.J.Biomedical Eng.Res.，2005，22（5）：1078-1081.（in Chinese）

［4］周永新，罗述谦.基于形状特征点最大互信息的医学图像配准［J］.计算机辅助设计与图形学学报，2002，14（7）：654-658.ZHOU Y X，LUO SH Q.Medical image registration based on mutual information of feature points［J］.J.Computer-Aided Design＆amp;Computer Graphics，2002，14（7）：654-658.（in Chinese）

［5］张红颖，张加万，孙济洲.改进Demons算法的非刚性医学图像配准［J］.光学 精密工程，2007，15（1）：145-150.ZHANG H Y，ZHANG J W，SUN J ZH.Non-rigid medical image registration based on improved Demons algorithm［J］.Opt.Precision Eng.，2007，15（1）：145-150.（in Chinese）

［6］吴元昊，于前洋.基于傅里叶相位差的抗噪声位移估计算法［J］.光学精密工程，2007，15（7）：1137-1142.WU Y H，YU Q Y.Denoising algorithm of displacement estimation based on phase difference of Fourier transform［J］.Opt.Precision Eng.，2007，15（7）：1137-1142.

［7］杜登崇，蒋晓瑜，姚军.基于相位相关的电子稳像算法研究［J］.激光与红外，2009，39（1）：63-66.DU D CH，JIANG X Y，YAO J.Electronic image stabilization algorithm based on phase correlation［J］.Laser＆amp;Infrared，2009，39（1）：63-66.（in Chinese）

［8］李治国，安锦文，赵银铃.基于相位相关的全局运动估计算法［J］.计算机测量与控制，2008，16（4）：532-534.LI ZH G，AN J W，ZHAO Y L.Global motion estimation algorithm based on phase correlation［J］.Computer Measurement ＆amp;Control，2008，16（4）：532-534.（in Chinese）

［9］黎俊，彭启民.范植华.亚像素级图像配准算法研究［J］.中国图象图形学报，2008，13（11）：2071-2075.LI J，PENG Q M，FAN ZH H.Asurvey of sub-pixel image registration methods［J］.J.Image and Graphics，2008，13（11）：2071-2075.（in Chinese）

［10］徐宝昌，陈哲，赵龙.一种改进的最小二乘景象匹配算法［J］.北京航空航天大学学报，2005，31（8）：848-852.XU B CH，CHEN ZH，ZHAO L.Inproved least-squares acene matching algorithm［J］.J.Beijing Uniυersity of Aeronautics and Astronautics，2005，31（8）：848-52.（in Chinese）

［11］FOROOSH H，ZERUBIA J，BERTHOD M.Extension of phase correlation to sub-pixel registration［J］.IEEE Trans.Image Processing，2002，11（3）：188-200.

［12］SEITZ P.Optical superresolution using solid-state camera and digital signal processing［J］.Optical Eng.，1988，27（7）：535-540.

［13］KUGLIN C D，HINES D C.The phase correlation image alignment method［J］.Proc.IEEE 1975 Int.Conf.Cybernetics and Society，Sep.1975：163-165.

Sub-pixel registration of special and frequency domains for video sequences

SUN Hui，LI Zhi-qiang，SUN Li-na，LANG Xiao-long

（Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China）

To resolve the problems existed in the estimation of motion in video sequences，a novel method combining the gray projection in a spatial domain and the phase correlation in a frequency domain was proposed.Firstly，the gray projection algorithm was adopted to coarsely register images to entire pixel accuracy，which calculates the gray correlation function for the spatial domain in row and column orientations and obtains the pixel-level motion vector between two sequential images by comparing correlation characters.Then，the phase correlation algorithm was adopted to refinedly register images to sub-pixel accuracy，which uses power spectrum information of images to decrease the image dependence.Furthermore，the fitting method of parabo-loid surface based on least-square was used to fulfill the estimation of image displacement parameters.To verify the algorithm experimentally，some samples were simulated.The results show that this method can detect the displacement parameters accurately and efficiently，and can offer the image displacement in a accuracy of 0.01 pixel and the maximum registration error less than 0.004 8 pixel.

gray projection；phase correlation；image registration；sub-pixel level；motion detection

TP391.4

A

1674-2915（2011）02-0154-07

2010-10-11；

2010-12-13

国家973重点基础研究发展计划资助项目（No.2009CB72400607）

孙 辉（1963—），男，吉林柳河人，研究员，主要从事数字图像处理及计算机仿真方面的研究。

E-mail：sunh@ciomp.ac.cn