一种解决多处理机问题的混合算法的研究

方加娟，黄春华

（郑州职业技术学院，郑州 450121）

一种解决多处理机问题的混合算法的研究

方加娟，黄春华

（郑州职业技术学院，郑州 450121）

0 引言

今天计算机都向并行化、网络化、智能化进军，但随之而来的是并行分布式计算这一道难题。要解决并行分布式计算，就要合理地解决分布式系统中的任务高度问题。要在有限时间内求得分布式系统中的最优化调度，就要寻找到一种解决最优化的算法。过去都是采用蚁群算法，但蚁群算法有不能很好处理动态请求、数据挖掘中的数据分类聚类、规则发现、在线事务处理等问题，甚至还会出现停滞现象，所谓的停滞现象就是说当搜索到一定程度时，得出的结果是不真实的，所有个体所得到的结果是完全一致的。本文在析蚂蚁任务分配模型的基础上，提出加入遗传算子对其模型进行改良，提出一种解决多处理机问题的混合算法的解决机制。

1 蚂蚁任务分配模型

蚂蚁任务分配模型来源于蚂蚁的群体智能，在日常生活中，我们会发现多个单一的蚂蚁经常会通过协同作用来解决比较复杂的问题，他们通过分配任务来完成不同的任务来解决复杂的问题。我们假想处理机就是一只蚂蚁。要设计出蚂蚁任务分配模型，先要对处理机问题作些约定。即假设：每台处理机同时只能处理一个任务，每个处理机是相同的；任务是连续的，存在优先约束；一个任务不能同时在不同的处理机上进行处理等等。

定义1：一个蚂蚁代表一个处理机，每个蚂蚁包含有它所代表的处理机的所有属性和信息，还可能包含它自身的一些信息，如当前的位置、当前的状态、少量的过去信息的记忆等。

定义2：人工蚂蚁（处理机）的状态

sti≤0表示处理机Pi当前是空闲，sti≥1表示处理机Pi当前忙碌，且此时statei为Pi的处理时间。

定义3：人工蚂蚁的活动空间

用网格Grid＝[0.. w (n)－1]×[0.. h (n)－1]表示人工蚂蚁的活动空间，它是所有格点(x，y)构成的二维数组，其中x∈[0.. w (n)－1]，y∈[0..h (n)－1]，h (n)∈Z+是关于人工蚂蚁个数n的函数。

定义4：调度选择概率

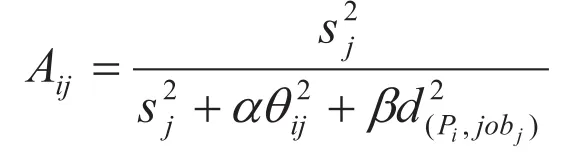
Aij表示处理机Pi响应需求浓度为Sj的jobj的概率，Sj是jobj的需求强度值，用来表示jobj的需求迫切程序。

定义5：蚂蚁任务分配模型

蚂蚁模型任务分配用一个五元组来表示，即TAM＝(Grid, State, n, m, DAG)。这里Grid代表二维网格，即agent所在的活动空间；State表示agent(即处理机)的有限状态集；m表示任务的个数，n为处理机的个数，也是agent的个数；DAG为表示任务间关系的DAG图G ＝J, E, Et。

基于蚂蚁任务分配模型的多处理机的调度过程如下：

1）将所有的处理机P（即人工蚂蚁）随机放置到网格Grid的某些格子中，同时将任务job随机放置到网格Grid的某些格子中。计算每个处理机P到每个任务job的之间的距离d (Pi，jobj)。

2）设置系统时钟，确定算法结束时间tnax。在(0, tnax)时间内，处理机将循环处理任务序列。但是，当任务序列处理完成后，算法输出这次的处理机调度序列，同时开始下一轮的处理机调度。在时间到达tnax后，在众多的输出结果中，选择出最优解。

2 混合蚁群算法

蚂蚁任务分配模型中存在着处理动态请求、数据挖掘中的数据分类聚类、规则发现、在线事务处理等问题，我们在蚁群算法中加入遗传算子，设计了混合蚁群算法。

要将遗传算子加到蚂蚁任务分配模型中去，我们就要解决交叉算子、繁殖算子。变异算子的问题。我们先假设在调度中每个处理器上的任务是按高度升序进行的。如果交叉点的选取使得每个交叉点两侧任务的高度不一样，并且交叉点前面最优任务的高度而是一样，那新生成的符号串有效。任务Ji的高度为max (Heignt (Ji))＋1和max (Heignt (Ji))－1之间的一个随机数。我们认为具有较高适应度值的符号串应有更多的机会存活下来，通过从旧的群体中选取较高适应度值最大的符号串来构成新的群体，进尔实现繁殖。由随机交换两个高度相同的任务来实现变异。

混合算法的实现部分关键代码如下：

3 实验结果与分析

我们最主要是将混合蚁群算法与遗传算法在搜索能力方面进行比较分析。

为了研究需要我们对两种算法中的部分参数进行假设。遗传算法中解的群体规模为10，杂交和变异概率分别为pc＝1.0和pm＝0.04，算法的最多迭代代数1000代，内部杂交概率为pINCX＝0.7，迁移概率为pmirgration＝0.3。而混合蚁群算法中的DAG图是随机生成的，每个节点有1-4个后继，估计运行时间为1-50的随机数，演化策略中的参数为 /＝4。各处理机之间数据传输延时也是随机生成的。当算法能收敛到全局最优解时，运行时间通常在2s以内，当算法不能收敛到全局最优解时，就会一直进化到预先设置最多迭代代数，所用的时间用minmaxtime来表示。

我们通过比较遗传算法和混合蚁群算法在处理机数为2，任务数为20个的情况下和处理机数为3，任务数为20的情况下的静太性能曲线。通过比较我们会发现混合蚁群算法会更快更好地逼近最优值，更容易找到最佳方案，而且有一定的稳定性。我们认为混合蚁群算法更适合解决多处理机问题。图中的横坐标X表示进化代数，纵坐标Y表示任务完成时间。从图中可以看出混合蚁群算法更快地逼近最优解，而且稳定性也更好。

图1 算法的静态性能曲线（m＝2，n＝20）

另外，我们还利用Job-Shop中的常见问题

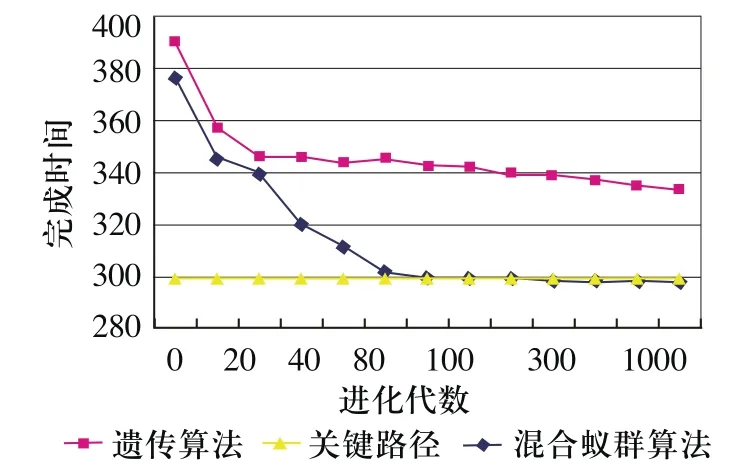
图2 算法的静态性能曲线（m＝3，n＝20）

MT06和MT10来比较引入遗传算子(IJSA入遗传算子(JSA)的基于TAM的蚁群算法的效率。

图3 两种蚁群算法的minmaxtime比较

从图3要可以得到，混合蚁群算法能找到更好的解，该算法不仅使优先约束的要求得到满足，而且可以最大限度的保留原有调度中的任务优先顺序，从而使优良的计算结果得以保存。在算法JSA中添加遗传算法中的混合蚁群算法IJSA相对于原算法JSA可以更快的收敛，且不容易陷入局部最优解。

蚂蚁在网格中动态地响应任务、处理任务。而任务也可以有一个产生、处理、完成的动态过程。因此，混合算法任务分配模型完全可以用到动态任务调度中，模型可以通过一定的机制将动态调度中不断出现的任务依次放入网格中，根据任务的属性不同，赋予不同的响应度，就可以实现动态调度，改进后算法的灵活性和健壮性提高了很多。

[1]张拥军, 张怡, 彭宇行, 陈福接.一种基于多处理机的容错实时任务调度算法[J].计算机研究与发展, 2000, 37(4):425-429.

[2]俊奇. 基于多处理机系统的最短路径并行算法的高效实现[J]. 计算机系统应用, 2009, 18(10): 76-80.

[3]单汨源, 张冠群, 晏敏, 吴娟. 一种求解多模式资源受限项目调度问题的新方法[J]. 科技管理研究, 2009(6).

The research of an hybrid algorithm in task scheduling problems

FANG Jia-juan, HUANG Chun-hua

并行处理在各行各业的发展非常迅速，而要解决并行处理过程中的调度问题不是件容易的事，最近几年越来越多的研究生加入到这个队伍中来，并加以研究。本文提出一种加入遗传算子的混合蚁群算来解决多处理机问题，避免了传统的蚂蚁任务分配模型的缺点。

多处理机；蚂蚁任务分配模型（TAM）；遗传算法

方加娟（1975－），女，河南郑州人，讲师，研究方向为计算机技术及应用。

TP391

A

1009-0134(2011)4(下)-0140-03

10.3969/j.issn.1009-0134.2011.4(下).41

2010-12-15