SINS/GPS紧耦合系统可观测性分析

刘 飞，胡小毛，翁海娜，李士心

(天津航海仪器研究所，天津 300131)

以伪距、伪距率作为观测量的SINS/GPS紧耦合组合方式是一种相对复杂的高水平的综合，GPS接收机提供伪距、伪距率给融合算法并用于系统校正[1-2]．卡尔曼滤波是 SINS/GPS组合导航系统处理数据最常用的算法，滤波有效性取决于系统的可观测性．对于不完全可观测的系统，不仅要知道每个状态变量的可观测性，还要知道每个状态变量的可观测程度．对于线性时变系统，无法直接用定常系统的可观测性判据来进行可观测性分析，当只需分析系统可观测性时，可采用分段线性定常系统(piece-wise constant system，PWCS)可观测性分析理论与方法来定性地分析系统可观测性[3-4]．系统状态变量可观测度的定量分析方法目前可分为特征值方法[5]和奇异值分解方法[6]2类，前者是基于误差协方差阵特征值和特征向量的可观测度分析方法，后者是基于系统观测矩阵奇异值分解的可观测度分析方法．此外 Hong等[7]研究推导了一种适用于多输出时变系统的可观测性测量方法，陈哲[8]在 1991年首次给出了局部可观测性分析理论，并将其用于分析时变不完全可观测系统中某些时间段系统的可观测性．

下面给出可见卫星数大于 4颗时基于G˜矩阵选星算法的伪距、伪距率的 SINS/GPS紧耦合系统的系统状态方程和量测方程．

1.1 基于矩阵的选星算法

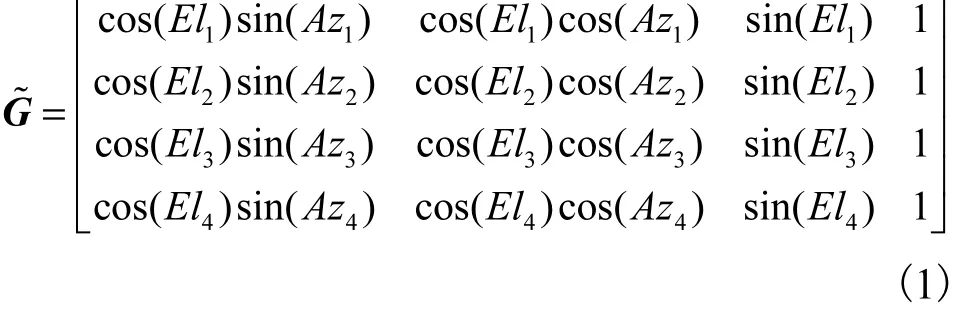
在 ENU坐标系中，第 i颗卫星与用户的单位方向余弦矢量可以表示为

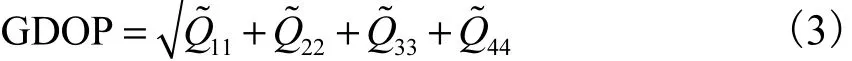
算法的基本思想是：从 N颗可见星中选出高度角大于 10°的卫星(假设高度角小于 10°的可见星数为k)，然后从N-k颗高度角大于10°的星座中选出高度角最大的卫星，进而从剩余的N-k-1颗可见星中选出3颗卫星的组合，与高度角最大的卫星组合成一组定位星座，利用 ENU坐标系下几何精度因子的计算公式计算相应的 GDOP值，选择 GDOP值最小的一组可见卫星参与导航定位．

1.2 SINS/GPS组合系统状态方程

SINS的误差状态为速度误差、姿态角误差、位置误差、陀螺漂移、加速度计零偏；GPS的误差状态，在伪距、伪距率组合系统中，通常取 2个与时间有关的误差：一个是与时钟误差等效的距离误差ut δ，另一个是与时钟频率误差等效的距离变化率误差rut δ ．组合系统状态方程为

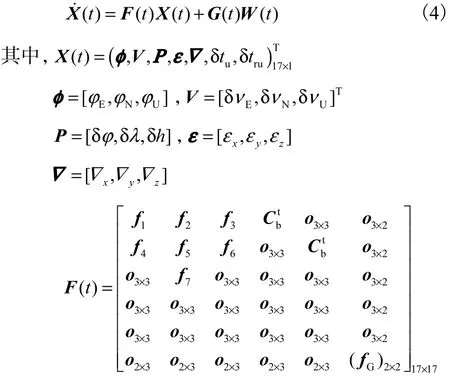
式中： fk(k =1,2,…,7)为3× 3阶非零时变矩阵；G(t)为17× 8维系统噪声驱动矩阵；W(t)为8× 1维系统激励噪声向量．

1.3 SINS/GPS组合系统量测方程

基于伪距、伪距率的 GPS/SINS组合系统的量测方程[9](i为参与导航定位可见卫星数，j为卫星号(j＝1，2，…，i))为

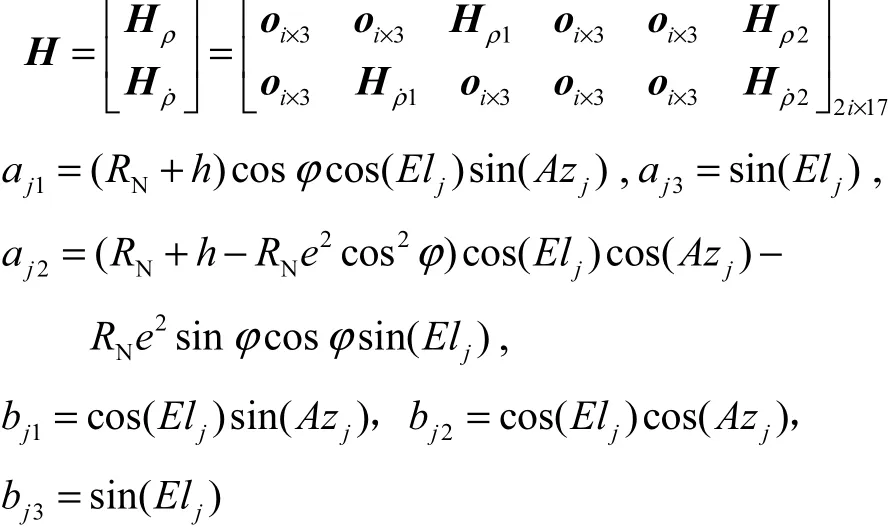
2 证明 SINS/GPS紧耦合系统满足 PWCS定理

2.1 PWCS可观测性分析定理

系统的可观测性分析结果与输入无关，故可使用离散线性齐次系统模型对系统进行可观测性分析．设齐次线性系统模型为

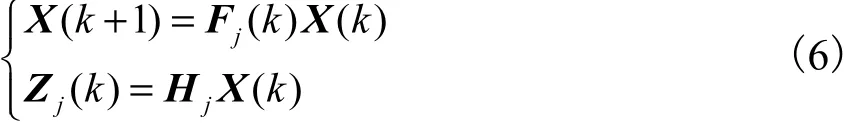
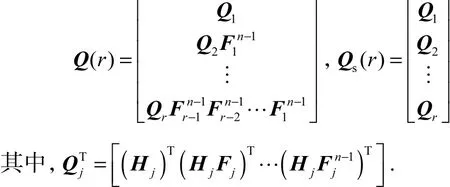
定理1的条件是 Fj中对应特征值1的特征向量属于 Qj的零空间．定理1说明，可用离散系统PWCS的SOM代替TOM研究离散系统的可观测性．

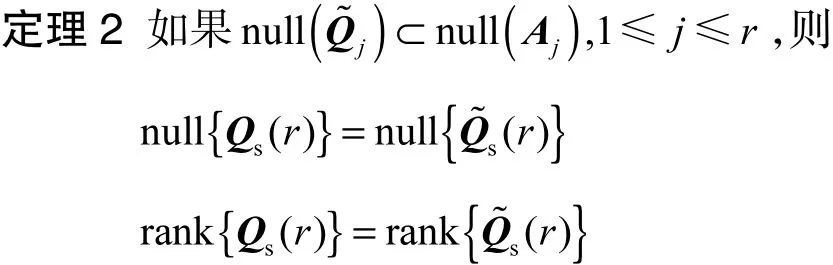
定理2说明，可用连续系统PWCS的SOM代替TOM研究连续系统的可观测性．

定理3 如果Fj是对应于Aj和Δj的离散化的转移矩阵，则

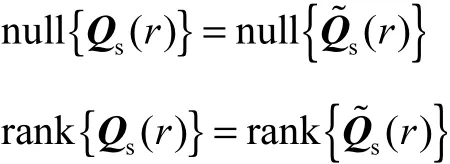
定理3说明，离散型PWCS和连续型 PWCS的可观测性分析是等价的．

定理1、2、3的证明过程见文献[3]．

2.2 证明SINS/GPS紧耦合系统满足PWCS定理

当可见卫星数大于4颗时，利用第1.1节的G矩阵的选星算法选出最佳的4颗导航定位卫星，此时由式(5)令 i＝4，即可得到 4颗可见卫星的 SINS/GPS紧耦合系统状态量测方程，为了证明系统满足定理 2的条件，通过重排系统的状态变量，得齐次分段式SINS/GPS紧耦合系统的状态量测方程为

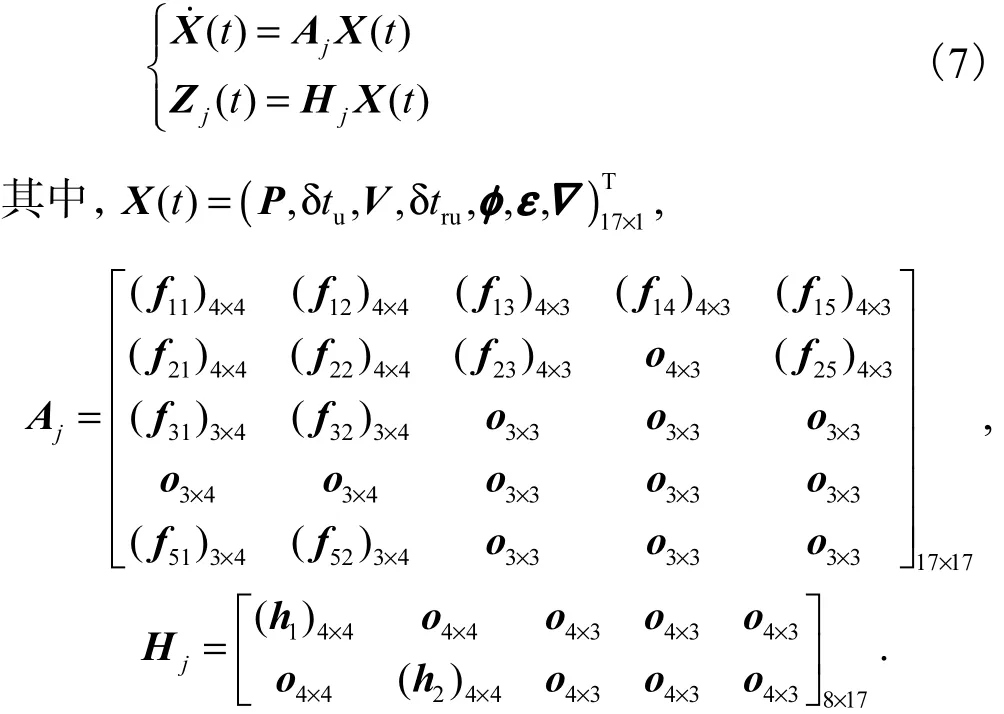
式中1h和2h均为可逆矩阵，由连续系统第j时间段的可观测性矩阵j定义可知

初等行变换不改变矩阵的秩和零空间，故设有非零向量其中各分量分别为 4、4、3、3、3维列向量．令X ∈ null(，则由式(8)有

定理 2的条件成立，故可以用连续系统的 SOM矩阵代替TOM矩阵进行可观测性分析，定理3说明连续型PWCS和离散型PWCS的可观测性分析是等价的，所以可知，可以用离散系统的 SOM 矩阵代替连续系统的TOM矩阵对SINS/GPS紧耦合系统进行可观测度的分析．

其他卫星数情况有类似分析证明过程．

3 基于G矩阵伪距伪距率的 SINS/GPS紧耦合系统可观测度分析

限于篇幅，仅给出直线平飞时系统的可观测度仿真分析结果．设初始位置为纬度 39.183°，经度117.113°，卡尔曼滤波率计算周期 0.01,s，GPS伪距测量误差为偏值 10,m，随机 25,m，随机伪距率误差为0.01,m/s，一阶马尔可夫过程相关时间为10,s．

图1和图2分别给出了第1时间段和第2时间段可见卫星数为 3颗的情况下系统状态变量的可观测度仿真结果(由于状态7、8的可观测度的相对其他状态数量级较大，故对状态7、8的可观测度在图1和图2中单独给出)，从第1时间段到第2时间段系统各个状态变量的可观测度有了明显的提高．可见卫星数为 1颗、2颗、4颗、6颗以及大于 6颗的情况有类似的分析结果．

表1给出了系统第1、2时间段(1#、2#)的可观测度仿真分析结果，为确保系统矩阵的变化量可以忽略不计，系统分段时间间隔应该取为较小值，本文时间段取0.5,s，由表1的结果可以看出，第1时间段参与导航定位的可见卫星数从 1颗增加到 6颗时，系统SOM 的秩分别为 7、11、12、13、13，系统的可观测性和可观测度随着卫星数增多而同时提高；第2时间段可见卫星数从1颗增加到6颗时，系统SOM的秩分别为 10、13、13、13、13，卫星数大于 6 颗时 SOM 的秩都为13，卫星数为1颗、2颗、3颗的情况系统的可观测性和可观测度进一步增强，卫星数为4的可观测性没有变化，进一步研究发现卫星数大于4颗的情况下系统的可观测性都不会变化，变化的只是系统各个变量的可观测度，随着时间段的增加，可观测度会进一步增强．再增加时间段的情况下，可见卫星数只有 1颗的情况下系统的可观测性和可观测度会同时提高，系统 SOM 的秩会提高到 11；可见卫星数为 2颗、3颗、4颗、6颗以及大于6颗的情况下系统可观测性没有变化，可观测度会有所提高．

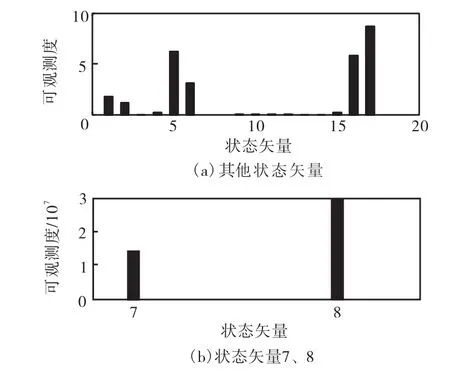
图1 3颗可见卫星状态可观测度(1#)Fig.1 Observable degree of states for SV＝3(1#)

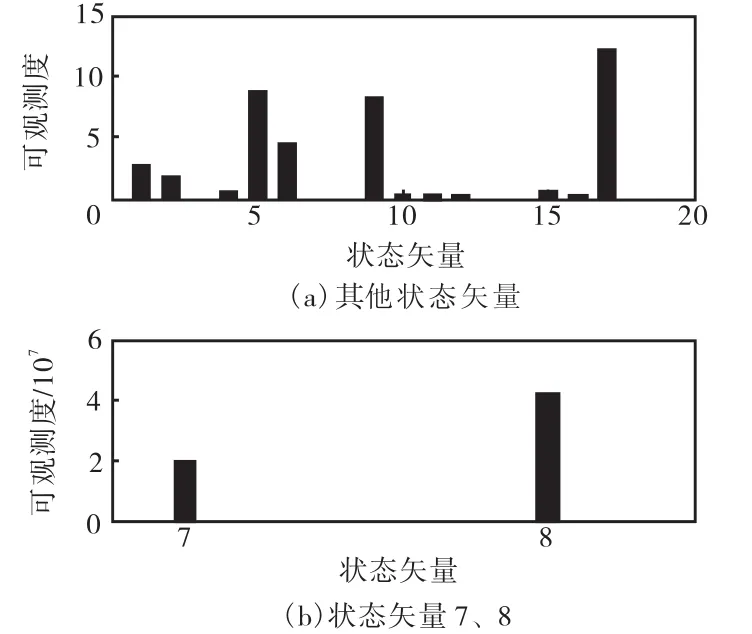
图2 3颗可见卫星状态可观测度(2#)Fig.2 Observable degree of states for SV＝3(2#)

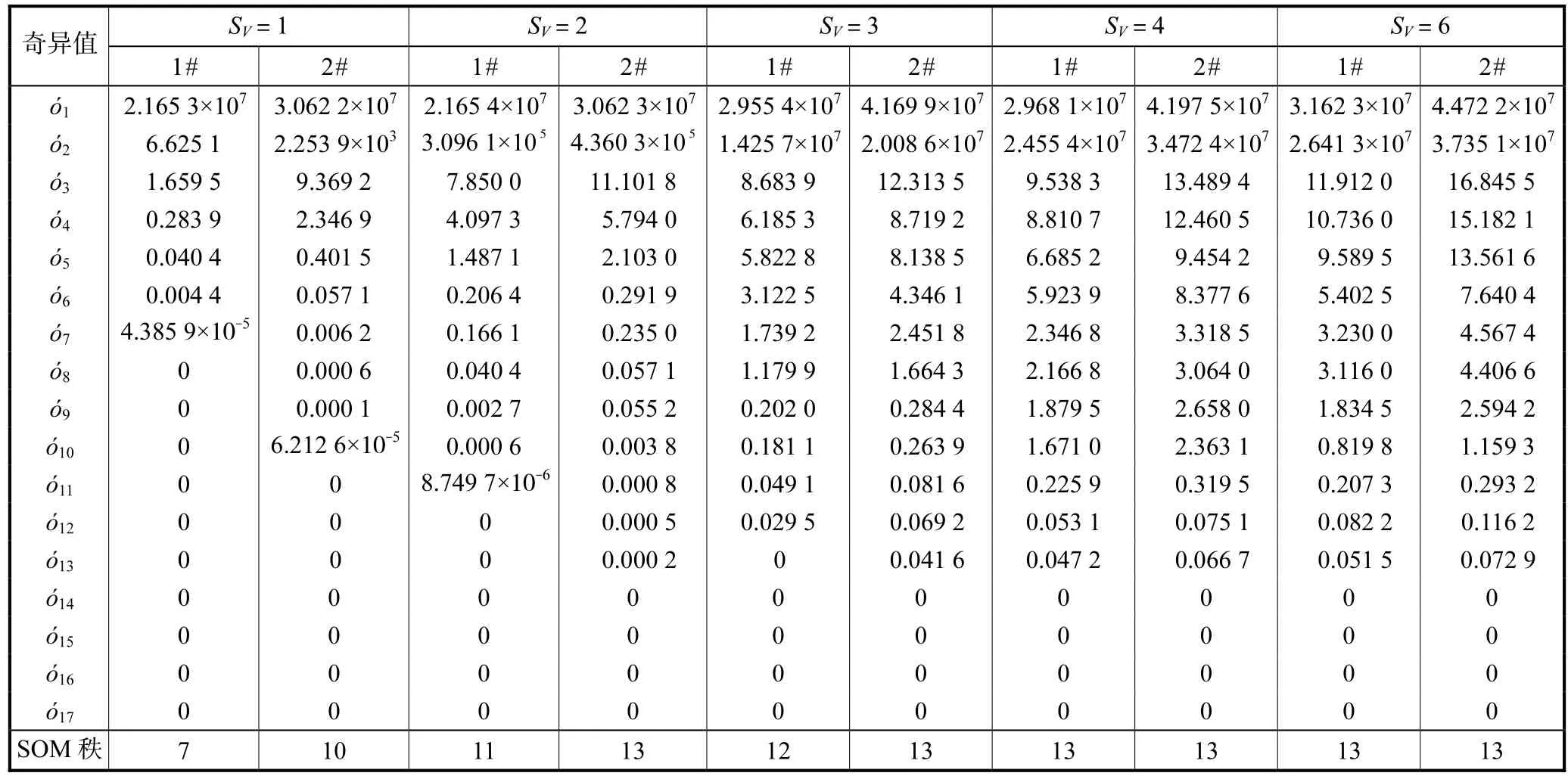
表1 系统状态可观测度(1#、2#)Tab.1 Observable degrees of system′s states(1#、2#)

4 结 语

利用 ENU 坐标系下几何精度因子的定义，在G˜矩阵选星算法基础上，给出了基于伪距、伪距率的SINS/GPS组合导航系统的状态和量测方程．通过PWCS理论和奇异值分解算法对上述紧耦合系统进行了仿真分析，结果表明，系统的可观测性和可观测度均与参与导航定位的可见星的数目有关系，为进一步研究SINS/GPS紧耦合系统提供先行技术支持．

［1］Schmidt G，Phillips R. “INS/GPS Integration Architectures，” and“INS/GPS Integration Architecture Performance Comparisons”[R]. NATO RTO Lecture Series，RTO-EN-SET-116，Low-Cost Navigation Sensors and Integration Technology，2008.

［2］Yang Yong. Tightly Coupled MEMS INS/GPS Integration with INS Aided Receiver Tracking Loops[D]. Department of Geomatics Engineering，University of Calgary，Calgary，Alberta，2008.

［3］Goshen-Meskin D，Bar-Itzhack I Y. Observability analysis of piece-wise constant systems(part I)：Theory[J].IEEE Transactions on Aerospace and Electronic Systems，1992，28(4)：1056-1067.

［4］Goshen-Meskin D，Bar-Itzhack I Y. Observability analysis of piece-wise constant systems(partⅡ)：Application to inertial navigation in-flight alignment [J]. IEEETransactions on Aerospace and Electronic Systems，1992，28(4)：1068-1075.

［5］Ham F M，Brown R G. Observability，eigenvalues，and Kalman filtering[J].IEEE Transactions on Aerospace and Electronic Systems，1983，19(2)：269-273.

［6］万德钧，房建成. 惯性导航初始对准[M]. 南京：东南大学出版社，1998.

Wan Dejun，Fang Jiancheng.Initial Alignment of Inertial Navigation[M]. Nanjing：Press of Southeast University，1998(in Chinese).

［7］Hong S，Chun H H，Kwon S H，et al. Observability measures and their application to GPS/INS [J].IEEE Transactions on Vehicular Technology，2008，57(1)：97-106.

［8］Chen Zhe. Local observability and its application in multiple measurement estimation[J].IEEE Transactions on Industrial Electronics，1991，38(6)：491-496.

［9］黄 昆，胡小毛. MINS/GPS组合导航系统选星算法[J]. 中国惯性技术学报，2009，17(6)：718-722.

Huang Kun，Hu Xiaomao. Algorithm of satellite selection used in SINS/GPS integrated navigation system[J].Journal of Chinese Inertial Technology，2009，17(6)：718-722(in Chinese).