高速列车测速测距系统滤波模型与融合策略研究

牛道恒 刘 岭 崔俊锋 陈志强

（北京全路通信信号研究设计院有限公司，北京 100073）

高速列车的测速测距系统要求能实时、连续、稳定地提供测速测距结果作为车载自动防护系统的控车依据。测速测距系统可使用多种测速传感器组合，包括惯性导航装置（INS）、转速计、多普勒雷达、GPS等[1,2]。以CTCS3-300T列控车载设备为例，目前采用的是2个转速计和2个多普勒雷达结合的多传感器系统构架。由于列车牵引力、制动力输出存在扰动，轨道摩擦、地面坡度等不断变化，列车的速度和加速度呈现复杂的变化过程；另一方面，传感器脉冲采集过程也存在噪声干扰。在测速测距处理模块中，需要对传感器输出信号的特征进行分析，建立适当的滤波模型以得到平滑的测速测距数据。同时，处理模块还要综合各传感器的工作状态和输出数据，得到融合后的测速测距结果。

1 测速测距系统结构与传感器工作原理

CTCS3-300T车载设备测速测距系统结构如图1所示。

图1中的每个脉冲采集单元连接1路转速计和1路多普勒雷达，它主要完成传感器脉冲信号的采集和基本调理，并将处理后的脉冲发送给测速测距处理单元；后者完成各路传感器的滤波处理和数据融合。

转速计又称车轮传感器，采用霍尔原理，车轮齿盘每转动一个齿距，转速计会产生一个计数脉冲。记齿盘共包含M个齿距，车轮直径为d。若在时间间隔T内共收到ptacho个脉冲，则由车轮运转线速度表示的列车速度为：

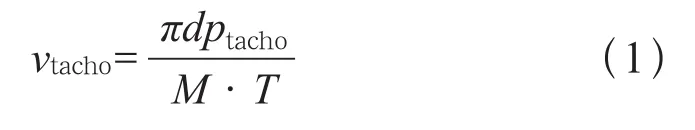
需要注意的是转速计会受到轨面粘着力的影响，如果发生空转打滑现象，需进行相应的处理或补偿。

多普勒雷达测速利用的是多普效应，通过发射波和地面反射波的频率差计算出列车和轨面的相对速度。记雷达的每公里脉冲数为N。若在时间间隔T内共收到pdopp个脉冲，则测得的列车速度可表示为：

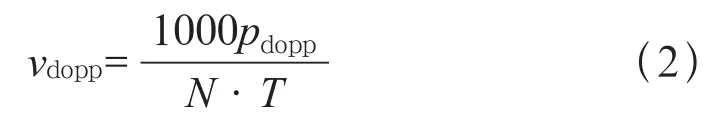
多普勒雷达测速的特点是不受车轮空转打滑及车轮直径变化的影响，但它对安装精度要求较高，且一般情况下较转速计更易受到干扰。

2 测速传感器滤波算法建模

应用于测速传感器的常见滤波算法有加权平均滤波[3]，粒子滤波[4]，H∞滤波[5],卡尔曼滤波[6,7]等。其中,卡尔曼滤波算法具有良好的性能，应用较为广泛。

卡尔曼算法的应用效果很大程度上依赖于滤波模型以及模型参数的选取。其离散模型的一般形式为：

其中，式(3)为状态方程，式(4)为观测方程；x(k)为状态变量，U(k)为激励变量，W(k)为过程激励噪声，z(k)为观测变量，v(k)为观测噪声。

算法的时间更新方程如式(7)和式(8)所示：

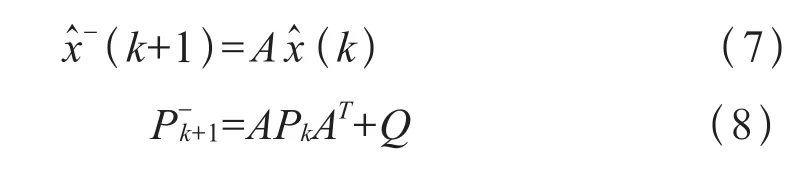
算法的状态更新方程如式(9)，(10)，(11)所示：

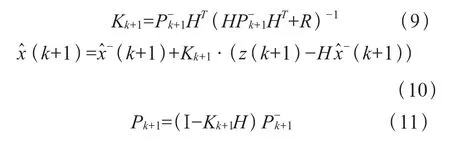
公式(3)～(11)为滤波算法的一般模型。针对图1所示的传感器建模时，状态变量可由速度v（k）和加速度v&（k）构成。激励信号U（k）可以理解为列车的牵引力或制动力，但对于测速测距单元而言，基本不可能获知U（k）的数据；考虑到列车牵引或制动力的变化是缓慢变化的信号，可以假定状态方程为恒加速模型，对应的状态变量 x（k）=[v（k）·v&（k）]T为二维变量。同样，如果速度采样的频率足够快，也可以认为列车速度本身即是缓慢变换信号，此时x（k）=v（k）为一维信号，对应的测速模型为恒速模型。

对于观测方程，转速计或雷达脉冲数是唯一可以直接观测的变量，即z（k）为一维变量。

两种模型的过程噪声方差Q和观测噪声方差R均通过现场数据拟合和仿真选取。

图2和图3分别给出了恒加速模型及恒速模型针对实验室和现场采集数据的滤波效果。

图2、图3中的v Sig代表从传感器脉冲观测到的速度信号，v Ref为参考速度信号，v Fil为采用上述卡尔曼算法模型得到的滤波结果。

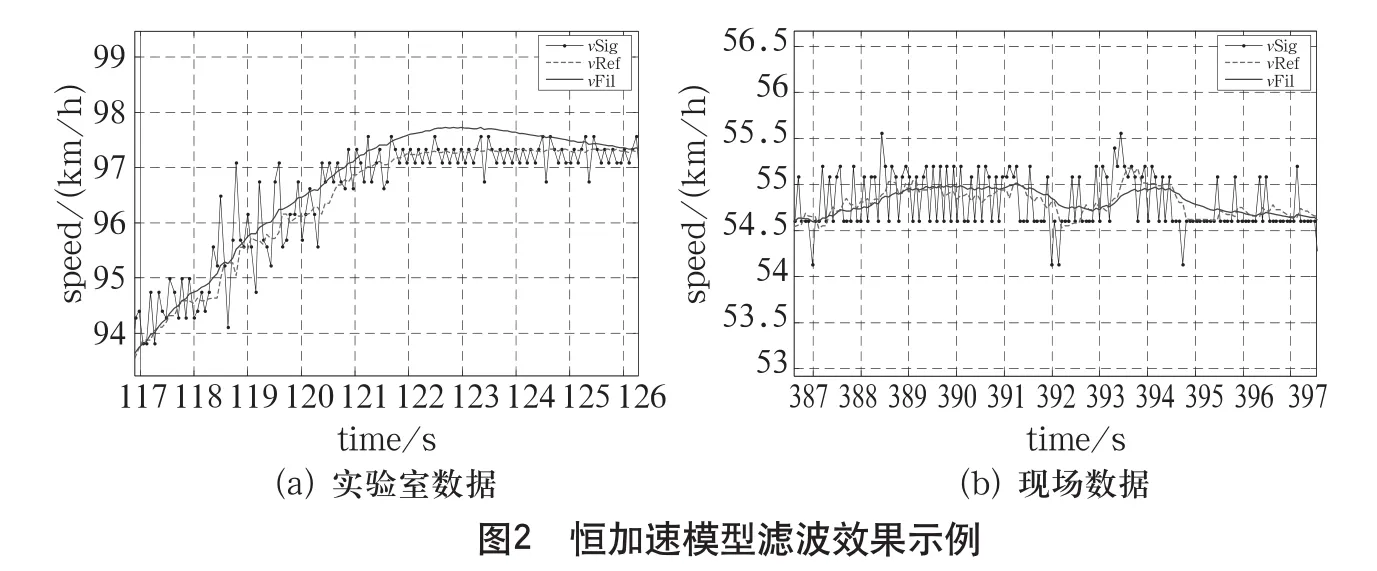
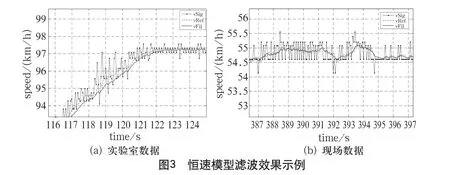
由图2(a)可知，对于实验室数据中加速度发生较大变化的临界点(正加速变为恒速)，恒加速模型会出现一定的“超调”现象，这是由于滤波的恒加速假设使得加速度变化较快时需要一段调整时间。由图3(a)可知，滤波结果对加速度变化不敏感，但对速度变化存在延时效应，这也与恒速模型的理论特性相吻合。

另一方面，由图2(b)、图3(b)可知，对于现场真实的加速度变化缓慢、速度变化缓慢信号，两种模型均能得到较理想的效果。

此外，噪声参数的选择会对算法的跟踪性以及平稳性带来影响，这两种特性之间存在一定的矛盾，需要根据滤波数据的特点进行平衡。

3 基于多路速度传感器融合的测速测距策略

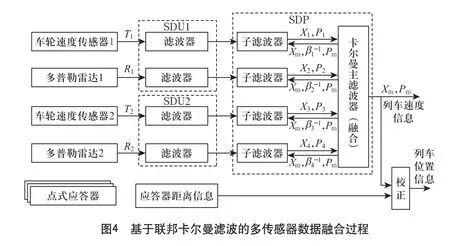
本文的前期工作提出了基于图1框架的联邦卡尔曼滤波融合模型[8]，如图4所示。

基于联邦卡尔曼滤波算法的融合方式在一定程度上利用了传感器之间噪声或者误差相抵的特性，其结果在理论上更接近状态变量的理想值。但对于高速列车而言，其设计理念是安全至上。故上述模型中若某个传感器检测出故障，需要对其进行隔离处理，即设置β为较小的数值(由于信息分配中存在β-1运算，不能设置为0)。

另一方面，若不同传感器之间滤波结果相差一定幅度(但在合理范围之内)，则应给测速值较高的传感器设置较高的β值。

同时，对于存在空转、打滑现象的转速计，或者存在高噪声的雷达传感器，应将其β值调整为较小值。

综上所述，应在图4所示的联邦卡尔曼融合算法的基础上，增加对各传感器信息分配系数β值的动态调整，以使得列车测速测距系统的安全性和鲁棒性得到进一步提升。

4 结语

基于转速计和多普勒雷达的卡尔曼滤波算法建模为测速测距系统算法及参数的选取提供了依据。仿真结果表明，对于现场缓慢变化的信号，恒加速模型和恒速模型选取适当的参数均能满足系统需求，但恒加速模型的跟踪性能更强。论文在联邦卡尔曼滤波算法基础上，提出了更适用于高速铁路安全需求的多传感器融合原则，为后续测速测距系统的研究提供了基础。滤波参数的优化选取和转速计空转打滑的补偿原则是论文未来的研究方向。

[1]陈艳华．轨道交通列车定位技术的选择与比较[J]．电子设计工程，2010，18(11)：186-188．

[2]董林．测速装置在地铁ATP中的应用[J]．铁道通信信号，2010，46(12)：20-22．

[3]铁道部科技情报所．武藏野编组站自动系统说明书．铁道科学研究院，1988．

[4]陈全，杨娟，唐伟．粒子滤波对火车车载测速系统的改进[J]．自动化技术与应用，2009，28(6)：56-58．

[5]陶建武，陶军，徐惠彬．基于鲁棒H∞滤波器的雷达测速方法[J]．计量学报，2006，27(1)：68-72．

[6]谭德荣，张莉，王艳阳．基于自适应卡尔曼滤波的轮速信号处理技术[J]．汽车工程，2009，31(6)：533-578．

[7] Kazuyuki Kobayashi，Ka C Cheok，rmjim W．Estimation of Absolute Vehicle Speed Using Fuzzy Logic Rule-based Kalman Filter[C]. Proceedings of the American Control Applications，NewYork，1995 ：281-284．

[8]黄卫中，季学胜，刘岭，李开成，牛道恒．CTCS-3级列控车载设备高速适应性关键技术[J]．中国铁道科学．2010，31(3)：22-25.