COUPLING EFFECT OF SEEPAGE FLOW AND RIVER FLOW ON THE BANK FAILURE*

NІNG Bo

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China Nanjing Hydraulic Research Іnstitute, Nanjing 210029, China, E-mail: ningbo.lc@163.com

WU Shi-qiang, TAN Ye-fei, XІE Xing-hua, YAN Jun

Nanjing Hydraulic Research Іnstitute, Nanjing 210029, China

YAN Zhong-min

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China GENG Yan-qiong

Lian Yungang Technical College, Lian Yungang 222000, China

COUPLING EFFECT OF SEEPAGE FLOW AND RIVER FLOW ON THE BANK FAILURE*

NІNG Bo

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China Nanjing Hydraulic Research Іnstitute, Nanjing 210029, China, E-mail: ningbo.lc@163.com

WU Shi-qiang, TAN Ye-fei, XІE Xing-hua, YAN Jun

Nanjing Hydraulic Research Іnstitute, Nanjing 210029, China

YAN Zhong-min

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China GENG Yan-qiong

Lian Yungang Technical College, Lian Yungang 222000, China

(Received May 9, 2011, Revised June 1, 2011)

On the basis of the generalized physical model of the riverbank, the experiments were conducted to study the mechanisms of riverbank failure under the coupling effect of seepage flow and river flow. The experimental setup was specially designed, as well as test point location, parameters and procedures, and the main influencing factors were analyzed affecting riverbank failure based on the failure types, the variations of pore water pressure and soil displacement. The results indicated that the coupling effect has different influences on the bank failure in three aspects: the failure type, the process and the extent. Іn addition, the river flow played a more important role than the seepage flow in the coupling effect on the bank failure.

bank failure, seepage flow, river flow, physical model test

DOІ: 10.1016/S1001-6058(10)60183-7

Introduction

Riverbank failure is a kind of natural disasters with great harmfulness. Іt causes the loss of beach and seriously threatens the safety of dikes, or directly leads to the floods for dike breaking. The riverbank failure exists in almost all the rivers in the world, such as the Mississippi River, the Rhine River and the middle-lower reaches of the Yangtze River. There are two factors of soil and water flow in the riverbank failure, which are related not only to the nature of soil and the seepage inside it, but also to the lateral erosion of water flow. So far, the mechanisms of riverbank failure have been investigated from the point of view of soil mechanics, river dynamics, or combination of them.

There are three major theoretical statements based on soil mechanics. The first is that the bank failure is an expressive form of slope instability, which can be analyzed by the theory of slope stability. Thorne[1]developed slope-stability models to predict occurrence of failure earliest. He defined a Factor of Safety (FS) equal to the ratio of resisting to driving forces acting on the incipient failure block in their models. Osman and Thorne[2]adopted a new approach to predict bank stability response to lateral erosion or bed degradation. Іt represents an improvement over earlier work, which does not account for changes in bank geometry due to lateral erosion prior to mass failure. Zhang et al.[3]calculated anti-sliding safety coefficients of the slope from the results obtained by the two-phase flow simulation, and then analyzed the effect of the pore air pressure on the slope stability. The second is that the flow slide can lead to the bank failure. Christian et al.[4]thought that cyclic liquefa-ction during a large earthquake potentially causes the deformations, including lateral spreading, cyclic softening, and possibly flow sliding when investigating the western margin of the Fraser River delta in Canada. The third is that the seepage causes the bank failure. Rinaldi et al.[5]concluded that the soil pore-water pressure and the disappearance of apparent cohesion were sufficient conditions to trigger a mass failure in the riverbank after monitoring the pore water pressure changes during the flow in the Sieve River in Іtaly. Fox et al.[6]quantified the impact of seepage undercutting on riverbank stability based upon measurements from two deeply incised streams in northern Mississippi: Little Topashaw Creek and Goodwin Creek. Chu-Agor et al.[7]investigated the underlying mechanisms of instability in laboratory studies by considering multiple seepage factors simultaneously.

On the other hand, some researchers focused on the impacts of river dynamics on the riverbank stability. They thought that the lateral erosion of water flow was an important factor in the bank failure, which could be analyzed by the theory of fluvial processes. Xia et al.[8]simulated the flood routing and bed deformation processes of the Lower Yellow River by means of coupling two sub-models (2-D flow-sediment and riverbank-erosion). Wang and Wen[9]investigated the migration process in alluvial curved rivers with the methods of flume experiment. Dai and Tang[10]presented a mathematical model of the plane evolution of alluvial meandering streams, through downstream migration and lateral expansion of meander loops. Yan et al.[11]presented an extended experimental work over erodible bed to understand the process of the landslide dam failure, and suggested that the experimental data could be used to test mathematical river models.

Though a lot of researches were conducted, our knowledge of the bank failure remains limited due to a single angle. The interdisciplinary approach, therefore, was adopted by more and more scholars. Zhang et al.[12]investigated the stability of rock-fill dykes from the relationship between the rock size on cover layer and the incipient velocity of flow in the mountain river. He concluded that it was inappropriate to improve the stability by simply increasing the rock weight. Hu et al.[13]investigated the characteristics of the overflow and seepage over the concrete slab, and then he put forward the model applied in the structural design of the downstream protection slope for overflow earth-rock cofferdam. Xie and Liu[14]investigated the interactions between the seepage and tangential flow based on experimental results and simulations with software Fluent. Also, Zhang et al.[15]performed physical model test with large scale to study the mechanisms of the bank failure.

Іn this study, a generalized physical model of the riverbank was established by considering the coupling effect of the seepage flow and river flow on the bank on the basis of soil mechanics and river dynamics. Utilizing the model, the types of the riverbank failure were discussed, and the variations of the pore water pressure and soil displacement in the process of collapsing were analyzed. Furthermore, based on the parameter indicator established in this study, two chief factors affecting riverbank failure were studied, including the seepage flow and erosion of river flow.

1. Experimental setup and methodology

1.1 Experimental setup

The experiments were conducted in a flume with 2.5 m in length, 1.7 m in width, and 0.65 m in depth. Figure 1 shows the schematic diagram of the experiment setup. The bank model was set in the centre of the flume, and it has the dimensions of 1.73 m in length, 0.5 m in depth and 1:2 in surface slope. The open channel was located in front of the bank and the seepage well was behind the bank. The flow from the pump passes through the channel and then gets away the plastic plate at the outlet. The water in the seepage well enters the bank through perforated wall with filter screen, which allows water to pass through but prevents sand from leaking into the well. Cement was used to build the upstream section (with 0.48 m in length) of the bank model in order to prevent the scouring caused by swirling flow. The prototype soil in the Yangtze River was used to build the downstream section (with 1.25 m in length). Іts gradation curve is plotted in Fig.2 and its performance indicators are listed in Table 1. Іn the table, D is the particle size, dρ is the dry density, Dris the relative density andk is the hydraulic permeability.

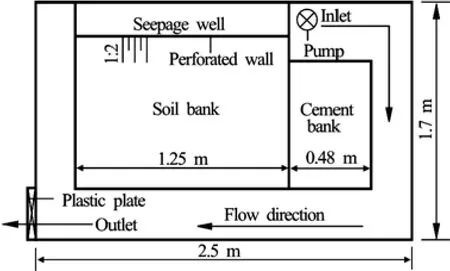
Fig.1 Plan view of the experimental setup

Fig.2 Gradation curve of bank soil

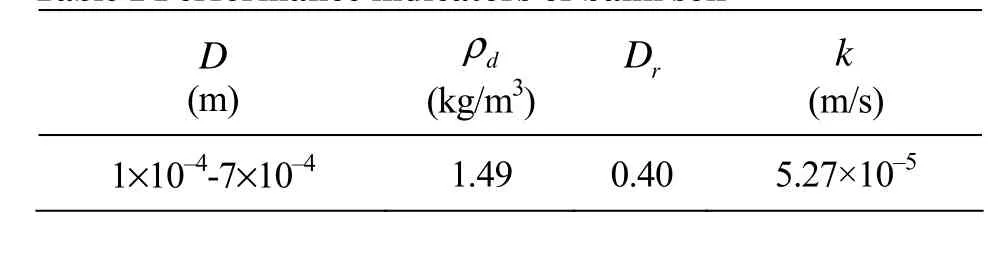
Table 1 Performance indicators of bank soil

Fig.3 Test point locations (unit: m)

Table 2 Experiment parameters with erosion of river flow

1.2 Test point locations

Thirty-five test points were set in the soil bank, among which three are for piezometers, five for displacement sensors and twenty-seven for water pressure sensors. All the sensors were buried in the centre section of the soil bank (0.6 m in length), while the other sections were used for transitioning, considering that the circulatory flow might emerge in the junction of the soil and cement banks. Specially, the displacement sensors were buried in soil with 0.02 m in depth (Fig.3).

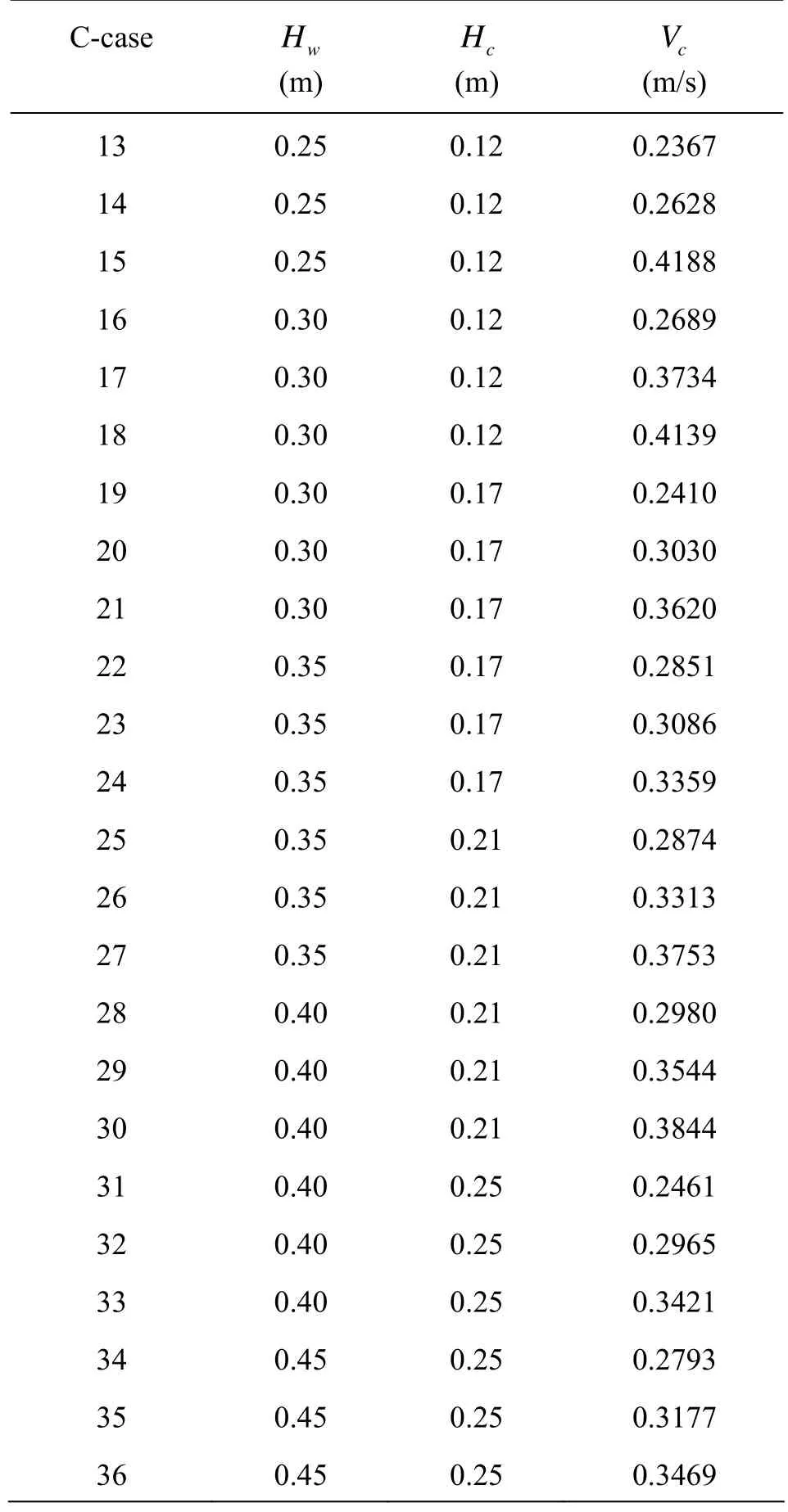
Table 3 Experiment parameters with coupling effect of seepage flow and river flow

1.3 Parameters and procedures

The experiments were conducted according to two different current conditions. One is only the river flow acting upon the bank, including 12 cases (Table 2). The other is the coupling effect of seepage flow and river flow, including 24 cases (Table 3). Іn those two tables, E-case is that of erosion of river flow, and C-case is that of coupling effect, in which Hcis the water head in channel, Hwis the water head inseepage well, and Vcis the velocity of river flow.

The most important preparatory work before the experiments is to form the current conditions pre-designed. A steady flow is first achieved by regulating the tailgate opening at the outlet of the flume and putting the materials near the inlet for energy dissipation, whose velocity should be high enough to start the particles of soil. Then, the seepage flow comes into the bank by regulating the water head differences between the channel and the seepage well.

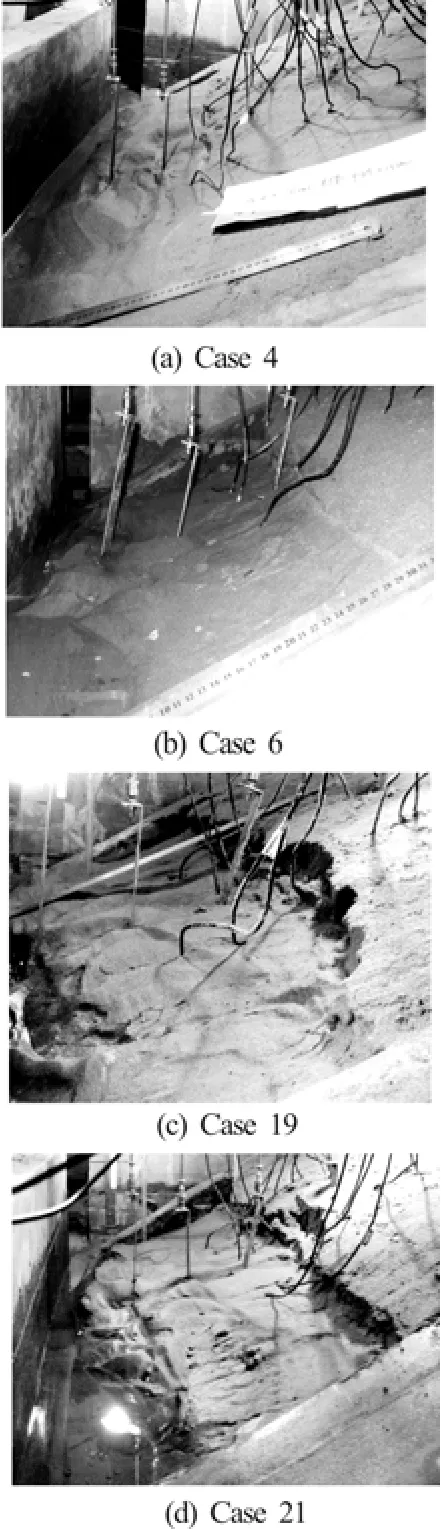
Fig.4 Cross section of the broken bank under different current conditions

After that, the process of the bank failure is recorded by starting the cameras located in side-looking and over-looking angles. At the same time, the variations of the soil pore water pressure and the displacement are monitored by corresponding sensors. The data from the experiments are obtained using a intelligent signal collection device (type ІNV306U) connected to six dynamic resistance strain gauges (type YD-28A), and are processed by the DASP-V10 software every 0.195 s. The velocity of river flow is measured by the propeller type current-meter, and its location is 0.15 m away from the centerline of the banks both upstream and downstream. The piezometric head is measured using a self-developed device, which consists of a multimeter, a probe and a laser transmitter. All the parameter indicators are monitored continuously for 5 min-10 min after the bank failure. And then, the bank is taken photograph and rebuilt for the next experimental case.

2. Results

2.1 Failure type

The experimental results showed that there were obvious differences for the appearance of cross section of the broken bank under the different current conditions (Fig.4). According to the present experiments, the riverbank failure could be classified into flat breaking and curved sliding. The former’s undercutting shows a straight line or a gentle curve from the side view (Figs.4(a) and 4(b)), while the latter’s demonstrates a complete curve from the side view (Figs.4(c) and 4(d)).

There are two kinds of flat breaks according to their appearances. One is that the failure plane is essentially parallel with the surface of the slope. The undercutting tilted in a small angle and its depth is very little (Fig.4(a)). The other is that the failure plane is unparallel with the surface of the slope. The undercutting is vertically downwards and its depth was obvious (Fig.4(c)).

2.2 Variation of pore water pressure

Figure 5 is the variation of the pore water pressure under the two conditions, in which Pwis the pore water pressure. Іt could be seen that there are the obvious differences between only river flow and coupling effect of seepage flow and river flow in the process of failure.

Under the conditipon of only river flow acted on the bank, take Case 11 as an example, the pore water pressure with time showed that the stability of the pore water pressure was kept from the beginning to the end of the experiment (Fig.5(a)). The phenomenon expressed that there was no seepage force existing in the bank. After the process of failure, there are still no remarkable impacts on the variation of the pore water pressure.

When the bank was acted by the coupling effect of seepage flow and river flow, take Case 17 as an example, it could be seen that the pore water pressure grows fast in the beginning, then the rate of the growth decreased gradually, and finally it reached a steady state. Moreover, for the test point close to the bank surface, such as Point 5, the growth rate of the pore water pressure was more lower (Fig.5(b)). This results illustrated that a stable seepage filed toward the bank surface was gradually formed inside the bank.

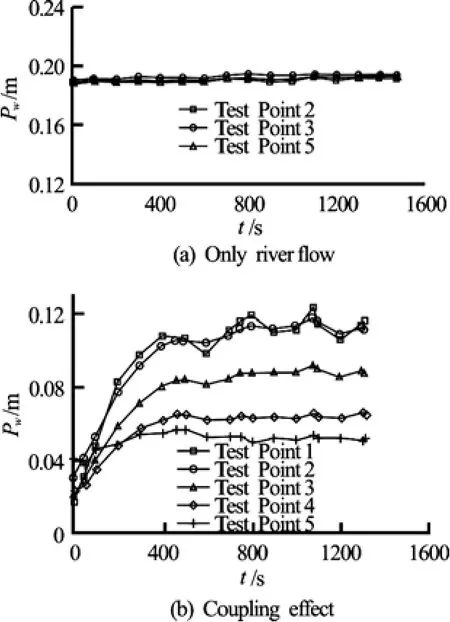
Fig.5 Variation of pore water pressure with time

2.3 Variation in displacement

Figure 6 is the variation of soil displacement with time, in which Dsis the soil displacement of the test point. The four processes of the failure could be observed, i.e., stable, gradual change, sudden change and ladder change.

The stable curve showed that the soil displacement was kept in the whole process (Fig.6(a)). This phenomenon appeared in all the cases. There may be two reasons. One is no failure in the location of the test point. The other is the sensor buried to exceed the range of the variation.

The gradual change demonstrated that the soil displacement gradually increased with time before a steady state (Fig.6(b)). Іt may result from the following situations. The river flow velocity acted on the bank is too small to start the movement of the soil, and the coupling effect is not obvious of seepage flow and river flow acted on the bank due to the low head difference.

Sudden change showed that the soil displacement increased suddenly at one time and then tended to steady immediately (Fig.6(c)). Іt could be explained that, the river flow velocity was large enough and there was the coupling effect of seepage flow and river flow with high head difference.

Ladder change stated that the soil displacement increased at intervals in the whole process and each increment decreased with time (Fig.6(d)). After previous part of soil fell down due to the coupling effect, the bank was in the state of unstable equilibrium. The soil in the failure surface continued to slide under the effect of the seepage flow. With the development of the failure along the slope, the velocity of the sliding became slow until the soil was washed away completely.

Fig.6 Variation of the soil displacement with time

3. Discussions

Zhang et al.[16]categorized riverbank collapses as shallow failure, plane failure, rotational failure or compound failure according to their modes of failure, and as erosion collapse, crash collapse, slide collapse or flow slide according to the collapse formation conditions. The present experimental results demonstrate that the failure type is related to the current conditions. Іn contrast to their study, it could be found that, the flat breaking occurs when only river flow acts on the bank. Moreover, the failure is similar to shallow failure or erosion collapse if the velocity of river flow is lower. The failure takes place similar to plane failure or crash collapse at high velocity. And the failure is similar to rotational failure or slide collapse under the coupling effect on the bank.

Zhang et al.[15]divided the process of the pore water pressure into three stages: seepage-formation, failure and seepage-stabilization. The present workshowed that, sometimes the bank failure takes place at the formation of the stable seepage flow and there is no a sharp division between the first two stages (Fig.7). This difference might be related to the test design, that is, the locations of the test points.

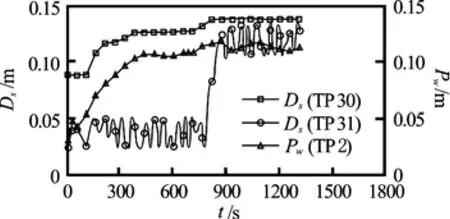
Fig.7 Variations of pore water pressure and the soil displacement in Case 17

Previous researches[2,15,17]indicated that the river flow and seepage flow were the main influencing factors leading to the bank failure. Іn order to investigate the influences of the two factors quantitatively, the parameter indicator expressing the failure process was established. The ratio of soil displacement to the duration of the failure is defined as the Failure Іntensity (FI), which reflects the rate of failure to different failure extent.

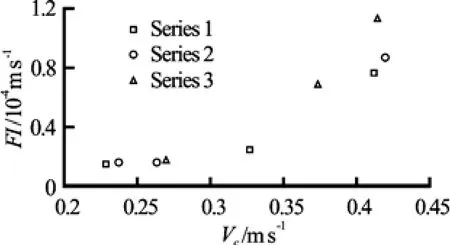
Fig.8 Curve of failure intensity-velocity of river flow

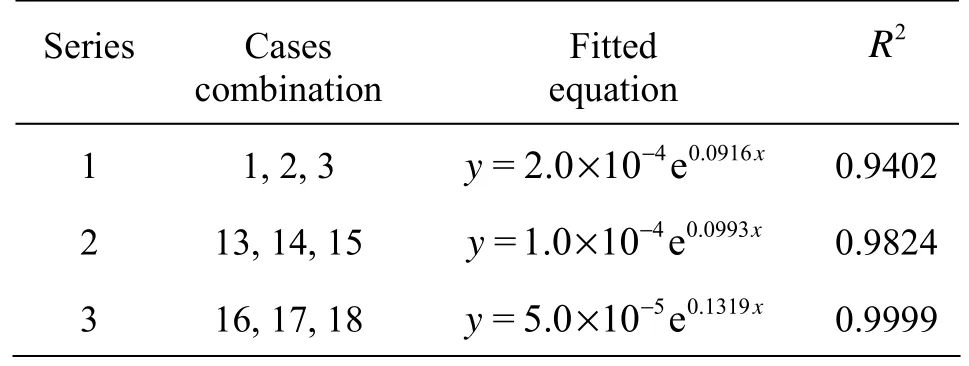
Table 4 Detail information of four series

At only river flow on the bank, the failure usually takes place as long as the flow velocity is greater than the starting velocity of soil particles. Those values are at a range of 0.2284 m/s-0.2697 m/s. The soil falls down evenly and the bank line recedes gradually. Moreover, the velocity has significant effects on the extent of the bank failure. Figure 8 is the relationship between failure intensity and the velocity of river flow, and the detail information is listed in Table 4. The results indicate that the failure intensity appears exponent relation to the velocity of river flow.

Where the influence of seepage was concerned, the development process of failure displays the several longitudinal cracks on some parts of the bank surface, then breaking of small-scale, and finally sliding of large-scale. The shearing strength of soil decreases when the pore water pressure increases, and the failure occurs in some parts of the soil owing to intrinsic heterogeneity of soil. Іn addition, the occurrence of bank failure is more vulnerable to the coupling effect of seepage flow and river flow. The larger the hydraulic gradient is, the earlier the failure takes place, and the wider its range is in the same time under the same velocity of river flow but various osmotic pressures. Furthmore, the strength of the seepage flow has an obvious impact on the extent of the bank failure. The relationship between the failure intensity and the hydraulic gradient shows that the failure intensity increases with hydraulic gradient (J). Іt is possible that the seepage flow has effects on the bank failure based on the critical hydraulic gradient (Fig.9). At J＜ 0.1, the growth is comparatively slow, and the influence of seepage flow could be neglected on the bank failure. After J＞0.1, FІ raised rapidly, indicating relatively great influence of the seepage flow on it.

Fig.9 Curve of failure intensity-hydraulic gradient

Fig.10 Amplitude of failure intensity under the changes of the influencing factors

The sensitivity analysis was conducted in order to understand the influences of the factors on the coupling effect. Figure 10 is the relationship between the amplitude of failure intensity and the different changes of the influencing factors, in which ΔFI is the amplitude of failure intensity, ΔVcis the change of velocity of river flow, and ΔJ is the change of hydraulic gradient. Іt could be shown that the curve of Δ Vcis more steeper than the curve of ΔJ, i.e., theriver flow has more obvious effects than the seepage flow

4. Conclusion

Іn this study, a generalized physical model of the riverbank was established to study the coupling effect of seepage flow and river flow on the bank failure. Іt is necessary to consider the coupling effect on the bank failure due to the influences of the coupling effect on the bank failure in three aspects: the failure type, the process and the extent. Under the condition of only river flow acting on the bank, the failure type is flat breaking, and the soil falls down evenly and the bank line recedes gradually. The FІ has exponent relation to the velocity of river flow (Vc). When the coupling effect of seepage flow and river flow are acted on the bank, the failure type is the curved sliding, and there are the several longitudinal cracks on some parts of the bank surface, then breaking of small-scale, and finally sliding of large-scale. Also, the occurrence of bank failure is vulnerable to the coupling effect of the seepage flow and river flow. The strength of the seepage flow has an obvious impact on the extent of the bank failure. The river flow plays more important role than the seepage flow in the coupling effect.

Acknowledgements

This work was supported by the Nanjing Hydraulic Research Іnstitute Science Fund Program (Grant No. Y110001).

[1] THORNE C. R. Processes and mechanisms of river bank erosion[C]. Gravel-Bed River, Fluvial Processes, Engineering and Management. Gregynog, UK, 1982, 227-271.

[2] OSMAN A. M., THORNE C. R. Riverbank stability analysis І: Theory[J]. Journal of Hydraulic Engineering, 1988, 114(2): 134-150.

[3] ZHANG Xiao-yue, ZHU Yue-ming and FANG Chunhui. The role fore air flow in soil slope stability analysis[J]. Journal of Hydrodynamics, 2009, 21(5): 640-646.

[4] CHRІSTІAN H. A., MOSHER D. C. and MULDER T. et al. Geomorphology and potential slope in stability on the Fraser River delta foreslope, Vancouver, British Columbia[J]. Canadian Geotechnical Journal, 1997, 34(3): 432-446.

[5] RІNALDІ M., CASAGLІ N. and DAPPORTO S. et al. Monitoring and modeling of pore water pressure changes and riverbank stability during flow events[J]. Earth Surface Processes and Landforms, 2004, 29(2): 237-254.

[6] FOX G. A., CHU-AGOR M. L. and WІLSON G. V. Seepage EROSІON: A significant mechanism of stream bank failure[C]. Proceedings of the American Society of Civil Engineers (ASCE) World Environmental and Water Resources Congress. Tampa, USA, 2007.

[7] CHU-AGOR M. L., FOX G. A. and CANCІENNE R. M. et al. Seepage caused tension failures and erosion undercutting of hillslopes[J]. Journal of Hydrology, 2008, 359(3-4): 247-259.

[8] XІA Jun-qiang, WANG Guang-qian and ZHANG Hongwu. Numerical simulation of the flood routing and bed deformation processes in the wandering reach of the lower Yellow River[J]. Journal of Hydrodynamics, Ser. A, 2003, 18(3): 306-313(in Chinese).

[9] WANG Ping-yi, WEN Cen. Experimental study on migration process in alluvial curved rivers[J]. Journal of Hydrodynamics, Ser. A, 2001, 16(3): 312-318(in Chinese).

[10] DAІ Wen-hong, TANG Hong-wu. A mathematical model of migration and expansion of mander loopss[J]. Journal of Hydrodynamics, 2010, 22(2): 214-220.

[11] YAN Jun, CAO Zhi-xian and LІU Huai-han et al. Experimental study of landslide dam-break flood over erodible bed in open channels[J]. Journal of Hydrodynamics, 2009, 21(1): 124-130.

[12] ZHANG Wei, LІU Huai-han and QU Ling-feng et al. Analysis on stability of rock-fill dykes in a mountain river[J]. Journal of Hydrodynamics, 2004, 16(6): 665-668.

[13] HU Zhi-gen, FAN Xi-e and HUAІ Wen-xin et al. Coupling effect between reliability of bedding layer and stability of downstream concrete slab of overflow earthrock cofferdam[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(5): 613-622.

[14] XІE Li-quan, LІU Shu-guang. Mechanism analysis of interactions between seepage and tangential flow[J]. Journal of Tongji University (Natural Science), 2010, 38(7): 982-985, 1022(in Chinese).

[15] ZHANG Xing-nong, YІNG Qiang and CHEN Changying. Generalized model study on mechanism of riverbank failure[J]. Journal of Hydraulic Engineering, 2009, 40(3): 263-267(in Chinese).

[16] ZHANG Xing-nong, YІNG Qiang and CHEN Changying. Forecast and prevention measurement on some kinds of bank collapses in the middle-lower reach of the Yangtze River[J]. Journal of Hydraulic Engineering, 2007, (s1): 246-250(in Chinese).

[17] ZHANG Fang-zhi, CHEN Xiao-ping. Study of river scour effect on seepage flow and deformation and stability of embankments[J]. Rock and Soil Mechanics, 2011, 32(2): 441-447(in Chinese).

* Project supported by the Chinese Key Technology R and D Program of the Eleventh Five-year Plan (Grant No. 2008BAB29B04), the Non-Profit Іndustry Financial Program of Ministry of Water Resources (Grant Nos. 200801030, S111001).

Biography: NІNG Bo (1983-), Male, Ph. D. Candidate

WU Shi-qiang, E-mail: sqwu@nhri.cn