基于MTI技术改善雷达识别目标性能方法

2011-05-08朱泽锋王鹏宇

电子科技 2011年12期

朱泽锋，王鹏宇

(中国人民解放军91913部队技术室，辽宁大连 116041)

1 多普勒处理和运动目标指示概述

多普勒处理是指对接收到来自某一固定距离单元、一段时间内的信号进行滤波或谱分析处理。一般来说，来自一个距离单元的慢时间信号的频谱包含着噪声、杂波以及一个或多个目标信号。接收机噪声在整个频谱范围内均匀分布。杂波占据了谱的一部分。谱中以杂波作为主要干扰的部分通常称为杂波区，以噪声作为主要干扰的谱区称为清洁区。杂波区和清洁区之间的过渡部分被定义为过渡区。在过渡区内，噪声和杂波都是主要的干扰源。静止目标出现在零多普勒频率处，而运动目标出现在谱的任何位置，这个位置取决于目标相对于雷达的径向速度。多普勒处理用于在多普勒域分离目标和杂波信号。杂波信号可以被直接滤除，保留下来的目标信号便成为最强的信号，或把多普勒谱直接计算出来，而位于杂波区外的目标信号就可根据超过噪声电平的频率分量被检测出来。

运动目标指示(MTI)是指完全在时域对慢时间信号进行处理。而脉冲多普勒处理是指在多普勒域对信号进行处理。MTI处理只需较低的运算量，但其获得的信息较为有限。脉冲多普勒处理要求较大的运算量，但能获得更多信息和更高的信干比。为便于把高速目标从静止目标和相对低速的目标中分离出来，以利于快速准确捕获和测量目标运动参数，需要采用MTI+多普勒处理的方式对接收机所接收的信号进行处理。

2 MTI的基本原理

雷达接收到的由M个连续脉冲组成的回波信号，经相干解调后的基带数据形成的一个二维数据矩阵，此矩阵对应雷达三维数据块的一个二维水平切面。也就是说，对每个天线，相位中心都接收一个类似的数据矩阵。对于一个单孔径天线系统或阵列天线的某一固定波束形成输出，只能形成单个二维数据矩阵。

二维数据矩阵中的每个列对应于对一个脉冲的连续采样，即连续的距离门。列中的每个元素都是一个复数，代表一个距离单元的实部和虚部分量。因此，二维数据矩阵中的每一行代表对同一个距离单元的一连串脉冲测量。快时间或距离维的采样率至少为发射脉冲的带宽，因此其量级为几百kHz到几十甚至几百MHz之间。慢时间或脉冲数维按雷达的脉冲重复间隔进行采样。因此慢时间维的采样率为PRF，其量级为几kHz到几十kHz，有时达到几百kHz。多普勒滤波是对矩阵的行数据进行操作。

MTI处理器对慢时间数据序列执行一个线性滤波处理，以抑制数据中的杂波分量。利用平台运动和场景的几何信息把杂波多普勒谱中心搬移到零多普勒谱频率处。然后利用高通滤波完成杂波衰减，保留了位于多普勒清洁区中的运动目标。MTI滤波和目标检测过程如图1所示。

图1 MTI滤波和目标检测框图

经过高通MTI滤波器的输出成为一个新的慢时间信号，它包含噪声以及可能存在的一个或多个运动目标信号。此慢时间信号再经过一个门限检测器。如果MTI滤波输出的信号幅度超过检测门限，则表明目标的存在。在MTI处理中只能给出目标是否存在的判决信息，并没有提供任何关于目标多普勒频率的估计信息，也没有提供目标径向运动方向的正负号信息。也就是说，它能够判断目标的存在，但不能确定目标多普勒频率的大小和方向。而且，它也不能提供目标存在的数目信息。如果多个运动目标同时存在于某个特定距离单元的慢时间信号中，MTI处理结果也仅给出“目标存在”的判决。另一方面，MTI处理简单、运算量较低。尽管处理形式简单，但一个精心设计的MTI处理器还是能够使信杂比(SNR)改善几dB到20 dB。对于某些杂波环境，如海杂波影响强烈的区域，甚至能改善更多。

3 MTI设计的主要任务与仿真分析

MTI设计的主要任务是选择所要使用的特定滤波器。典型的MTI滤波器是一个低阶、简单的形式。实际上，许多普通的MTI滤波器都是基于简单的探索式设计方法。假设一个固定雷达照射一个被理想静止杂波包围的运动目标。对于每个脉冲，其回波信号中的杂波分量都相同，而运动目标分量的相位会随距离的变化而改变。对连续脉冲对的回波进行相减，就可以完全对消杂波分量，而目标信号由于其相位的改变，通常不被对消掉或不被完全对消掉。因此，实现MTI的关键是设计合适的脉冲对消器[1]。

3.1 脉冲对消处理原理

当固定目标、海杂波与运动目标处于同一距离单元时，前者的回波通常较强，以至于运动目标的回波被“淹没”其中，故必须设法对二者进行区分。因固定目标回波中的多普勒频率为零，慢速运动的杂波中所含的多普勒频率也集中在零频附近，它们的回波经相位检波后，输出信号的相位将不随时间变化而变化或仅随时间作缓慢变化，反映在幅度上则为其幅度不随时间变化而变化或随时间缓慢变化[2-3]。相反，运动目标回波经相位检波输出后，因其相位随时间变化较大，反映在幅度上也是其幅度随时间变化而变化。因此，若将同一距离单元在相邻重复周期内的相位检波输出作相减运算，则固定目标回波将被完全对消，慢速杂波也将得到很大程度的衰减，只有运动目标回波得以保留。显然这样便可将固定目标、慢速杂波与运动目标区别开。这就是MTI对消的基本原理[3]。

3.2 脉冲对消器

为便于对脉冲对消器的基本原理进行理解，下面分别以二脉冲对消器和三脉冲对消器为例进行分析。图2为二脉冲对消器的流程图。

图2 二脉冲对消器的流程图

图2中，输入数据为对同一距离单元连续脉冲采样的基带复数据序列。x[n]是一个离散时间序列，其有效采样时间间隔t等于脉冲重复间隔。此线性有限冲激响应滤波器的系统函数为H(z)=1-z-1。把z=ej2πft代入系统函数中，得到以模拟频率F为变量的频率响应函数，即

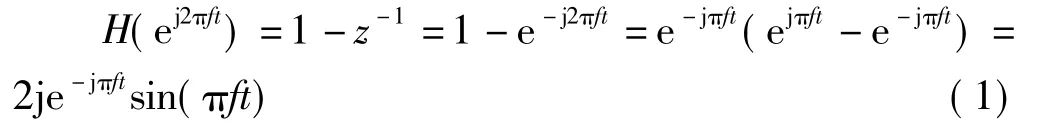
式(1)中，二脉冲对消器确实在零多普勒频率处起到了抑制杂波能量的作用，使得运动目标的谱分量或被部分衰减，或被放大，被衰减或被放大最终取决于谱分量在多普勒轴中的准确位置。

二脉冲对消器是一个简单的滤波器。它的实现不需乘法运算，每一个输出采样只需一次减法运算。然而，与理想的高通滤波器相比，它只是近似，但效果差。二脉冲对消器的一个常规改进就是三脉冲对消器，由两个二脉冲对消器级联得到。图3给出了二脉冲/三脉冲对消器归一化频率响应，三脉冲对消器能够明显地改善零多普勒附近的凹口宽度，但并不能改善非零多普勒频率处运动目标的响应。三脉冲对消器的每一个输出采样只需两次减法运算。

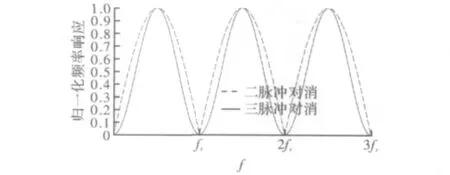
图3 二脉冲/三脉冲对消器归一化频率响应

尽管结构简单，但对于具有中等到较高脉冲相关性的杂波，二脉冲和三脉冲对消器是有效的。通过对杂波序列进行仿真研究可以得出以下结论:一个白噪声序列通过一个具有高斯功率谱的低通滤波器，在归一化频率上的标准差为整个频谱宽度的5%。杂波序列通过二脉冲对消器后，其功率衰减了13.4 dB，而对于三脉冲对消器，输出功率衰减了21.9 dB。

3.3 系统仿真分析

基于Matlab的雷达系统仿真框图，如图4所示。由于本系统只为仿真雷达系统处理部分，输入的是中频段回波。雷达发射采用线性调频信号，回波信号中包括2个速度为50 m/s和110 m/s运动目标回波，一个固定目标的回波用来检验MTI性能，信号淹没在系统噪声当中。接收信号首先经过数字正交解调得到I，Q两路信号，分别对这两路信号进行频域脉冲压缩处理，之后进行一次二脉冲对消，将对消后的信号进行多普勒滤波。滤波后经过数据处理就可得到速度和距离信息。

图4 雷达仿真系统框图

图5是正交解调后的波形，这时的信号脉冲和噪声混叠在一起无法分辨出有用信息。

图5 I，Q两路数据波形

由图6可见，在接收信号进行脉冲对消之前，运动信号与固定目标和噪声幅值大小难以区分，而经过MTI处理后，多数干扰被抵消掉，运动目标清晰的显示出来。对这样的信号进行多普勒滤波可以得到正确的目标信息。

图6 脉冲对消前后接收信号波形模值

图7是没有经过MTI处理的多普勒滤波结果，从图中可以看出，接收回波中的固定目标被误判为低速运动目标。

图7 未经MTI处理的多普勒滤波结果

图8显示的是经过MTI处理的多普勒滤波结果，与图7相比，固定目标经脉冲对消处理后被抵消，得到正确的运动目标信息。经计算速度信息有1.4%的误差，如果增加滤波器的组数，可以减小速度误差。MTI技术在雷达目标的识别、探测和跟踪过程中起着关键的作用。

图8 经过MTI处理的多普勒滤波结果

4 MTI技术运用实际

为改善复杂海杂波条件下雷达捕获被测目标的性能，某新型脉冲雷达采用4个二脉冲对消器级联的方式来消除海杂波对被测目标回波信号的影响。经过230 h对海杂波的特性录取和分析，提取出海杂波的平均多普勒功率谱，并以此作为门限，可极大地提高在强杂波干扰条件下捕获并连续跟踪被测目标的概率。对于径向速度＞3 m·s-1的目标，可达到99.9%以上的捕获概率。