超空泡图像的自适应多尺度小波边缘检测

雷 斌 ，侯帅格，沈艳辉

(西安工业大学电子信息工程学院，陕西西安 710032)

受水下环境和光源光照的影响，水下高速射弹试验获取的超空泡图像会夹杂很多噪声，要从中提取出精确的边缘信息，就必须选择合适的边缘检测方法。传统的边缘检测算子如Sobel算子、Roberts算子、Prewitt算子等虽然运算量小、速度快，但没有考虑噪声的统计特性。将这些传统算子应用于对水下射弹实验图像的边缘进行检测时，如果采用小模板，性能就会受到噪声较大的影响;如果采用较大的模板，虽然抗噪声能力较强，但又存在定位差等问题。Canny和Log算子，在边缘检测方面检测效果良好，能检测出更多的边缘，但自身的抗噪声性能很差，易受噪声的影响。

小波变换的优越性就在于其具有“变焦”功能，能多尺度地逼近边缘。小尺度下，得到非常细致的边缘，却夹杂一些噪声;大尺度下，得到较粗的边缘，滤除了大部分的噪声，也同时失去了许多的弱边缘。将不同尺度下的边缘信息进行融合，既克服了噪声干扰，又综合了强边缘和弱边缘，可以提取到更为有效和精确的边缘。

针对小波变换的优越性，采用自适应多尺度小波边缘检测算法对超空泡图像进行边缘检测。目前小波多尺度边缘检测算法的研究中，阈值的选择大致可以采用两种方法:一种是采用人工阈值，计算阈值的方法凭借经验取得，无法避免人为干扰，缺乏一定的理论依据，即使设定的某一阈值针对某一图片是合适的，但针对其他图片却不适用，还要重新设定阈值。因此，不适合工程实际的要求;另一种是采用自适应的阈值，文献[1～3]采用将图像的可能边缘图像分成n×n的子块，对子块内的小波变换系数进行一定的统计计算，得到子块的阈值。这种自适应阈值方法的缺陷在于:阈值的初值和分块大小对边缘检测的效果影响较大，而且阈值初值、小波系数加权和的比例系数的确定尚没有一定的理论，需要根据实际情况调整得到。另外，也有文献采用其他自适应算法，比如文献[4]借鉴OTSU方法自动选择阈值，文献[5]采用小波系数模的极大值与尺度和某一常数的比值来确定阈值，改变常数值来调整边缘检测效果。在文献[6]中模糊c-均值聚类理论进行边缘点检测和文献[7]中的聚类技术来实现阈值自动选取的启发下，文中给出了基于K均值聚类的自动阈值边缘检测方法，该方法克服了参数多和需要反复调整的缺点，只需要设定合适的聚类个数和背景标记，即可自动得到阈值后的边缘。实验表明，达到了良好的自适应效果。在得到阈值后对多尺度下的边缘进行融合时，借鉴文献[8～11]和文献[12]的算法和思路，在结合具体的实现中，文中对通过高斯小波变换和B样条小波变换边缘检测得到的多个尺度下的边缘分别采用不同的融合策略。

1 多尺度自适应小波边缘检测原理

1.1 多尺度小波变换和相邻尺度边缘增强

首先定义两个小波，这两个小波由二维平滑函数θ(x，y)沿x和y方向求偏导数得到，即

通过改变s的大小，得到图像在不同尺度下的小波变换系数。

由于相邻尺度上的小波变换具有相同的属性，即相邻尺度的小波系数具有相同的符号，而噪声点不满足这个规律，因此可以将相邻尺度系数相乘[13-16]，判断其符号，以区分信号和噪声，达到去噪的目的。经过系数相乘，强边缘得到增强，而微弱的边缘和背景得到削弱。

基于以上理论，在多尺度小波变换环节，对超空泡图像进行3个尺度下的小波变换，得到3个尺度下水平和垂直方向的小波系数，将同方向的相邻小波系数相乘，通过判断相乘后的符号进行抑制噪声处理，从而得到增强处理后的两组小波系数，进一步计算可以得到两组小波模值和幅角。沿着幅角方向进行局部模极大值抑制，即可以得到两组可能的边缘。

1.2 自适应阈值边缘检测

如果对得到的两个相邻尺度下的边缘图像取同一阈值，将会把微弱边缘和噪声一并滤除。而且该阈值如果人工设定或固定不变，只能适应某一幅图的边缘分割，不具有自适应和普适性，会影响到边缘的提取效果和检测速度。在借鉴相关文献的基础上，针对超空泡图像的特征，采用K均值聚类作为自适应阈值策略。

K均值聚类是典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度越大。该算法认为簇是由距离靠近的对象组成，因此把得到紧凑且独立的簇作为最终目标。

假设有一组包含K个聚类的数据，其中第k个聚类可以用集合Gk来表示，假设Gk包含nk个数据(x1，x1，…，xnk)，此聚类中心为yk，则该聚类的平方差ek可以定义为

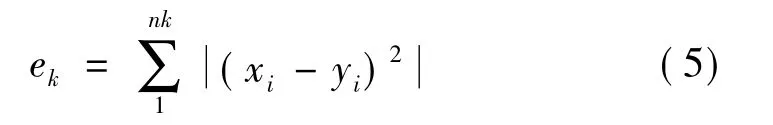
其中，xi是属于第k类的数据。而这K个聚类的总和平方差E是每个聚类的平方差总和。K均值聚类通过迭代的方式，设法降低E的值，以使得各聚类本身尽可能紧凑，而各聚类之间尽可能地分开。在实现中，对整个样本数据，进行迭代分类，最后得到聚类中心和各样本点的类别标记[17]。

经过非极大值聚类后的梯度图像中，背景和空泡边缘有明显的差别，因此可应用K均值聚类进行分类，实验发现如果分类数目为2，效果不好，因为弱边缘相对较接近背景，容易被归为背景类，因此可以通过扩大聚类数目来提高边缘检测效果，但是聚类数目过多也会带来不良后果。实验中，确定聚类数目为4～6，具体参数通过聚类效果设定。聚类后，得到梯边缘图像的聚类标记，结合聚类中心值，对聚类标记进行分析，将标记分为背景和边缘两类，最后再通过对标记的筛选来确定是否为边缘。

实验中，聚类数目为4、5、6时，观察聚类后的标记矩阵mask发现，mask(i，j)=1，非常接近背景，而其余标记接近边缘。因此对聚类后得到的标记矩阵进行逐点判断，如果mask(i，j)≠1，则Edge(i，j)=1;否则Edge(i，j)=0，以区分背景和边缘。实验中，还发现聚类数目为4和5时，对结果的影响不大，但当聚类数目为6时，会将部分背景和弱边缘聚为同类，边缘中夹杂噪声背景。

1.3 多尺度边缘融合

图像每个尺度的小波变换都提供了一定的边缘信息。当尺度小时，图像的边缘细节信息较为丰富，边缘定位精度较高，但易受到噪声干扰;当尺度大时，图像的边缘稳定，抗噪性能好，但定位精度差。解决方法之一是将各尺度边缘图像的结果综合起来，发挥各尺度的优势，得到精确的单像素宽的边缘[18]。

在实现中采用高斯函数和B样条函数分别对图像进行多尺度小波变换，并对变换后的可能边缘进行自适应阈值边缘检测，在融合算法的应用中，发现两种不同小波基的边缘不能同时适用于一种融合策略，在反复实验后，对高斯小波基得到的边缘采用融合算法1，B样条小波基得到的边缘采用融合算法2。

1.3.1 融合算法1的思路

以高斯函数作为小波基，对超空泡图像进行多尺度变换和自适应阈值边缘检测后得到Edge1和Edge2，其中Edge1和Edge2分别为尺度12和23边缘增强和自适应后的边缘。对Edge1和Edge2按照以下规则进行逐点分析，若满足则标记为边缘点，否则为非边缘点。

规则如下:

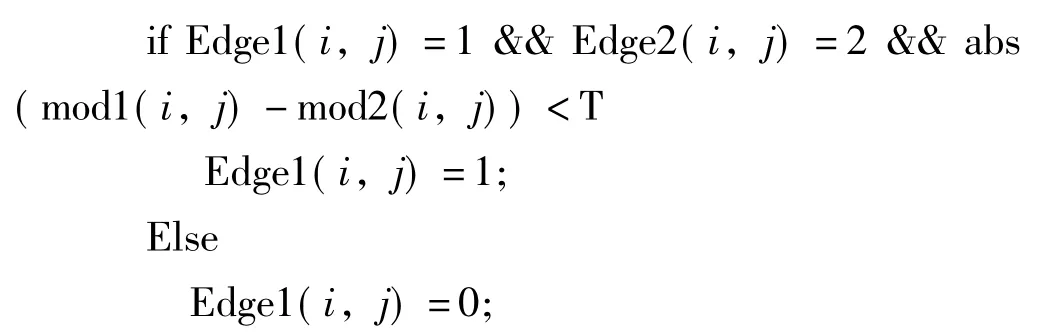
abs表示取绝对值运算，mod1和mod2为尺度12和23边缘增强和极大值抑制后的模值。T根据反复实验后最终边缘效果调整得到。

1.3.2 融合算法2的思路

(4)对融合小波系数mdx和mdy进行自适应阈值边缘检测，得到x，y方向的最终边缘Ex和Ey。

2 算法的总体流程和实现结果

在使用自适应多尺度小波变换对超空泡图像进行边缘检测中，以高斯函数和B样条函数作为小波基对图像进行小波变换，用K均值聚类对多尺度下的小波系数进行自适应阈值边缘检测，最终对多个尺度下的边缘进行融合，得到超空泡的边缘。

2.1 算法的总体流程

算法的具体步骤如下:

(1)选择小波基函数(高斯函数或B样条函数)。

(2)进行3个尺度下的小波变换，相邻尺度间进行增强和去噪。

(3)判断小波基函数，若为高斯函数，进行步骤(4)～步骤(7);否则使用多尺度融合算法2中的步骤得到最终边缘。

(4)计算各尺度下的模值和幅角。

(5)对各尺度下的模值进行非极大值抑制，得到可能的边缘梯度图。

(6)对各尺度下可能的边缘进行自适应阈值边缘检测，得到各尺度下的边缘。

(7)使用文中多尺度边缘融合算法1，得到最终的边缘。

算法流程如图1所示。

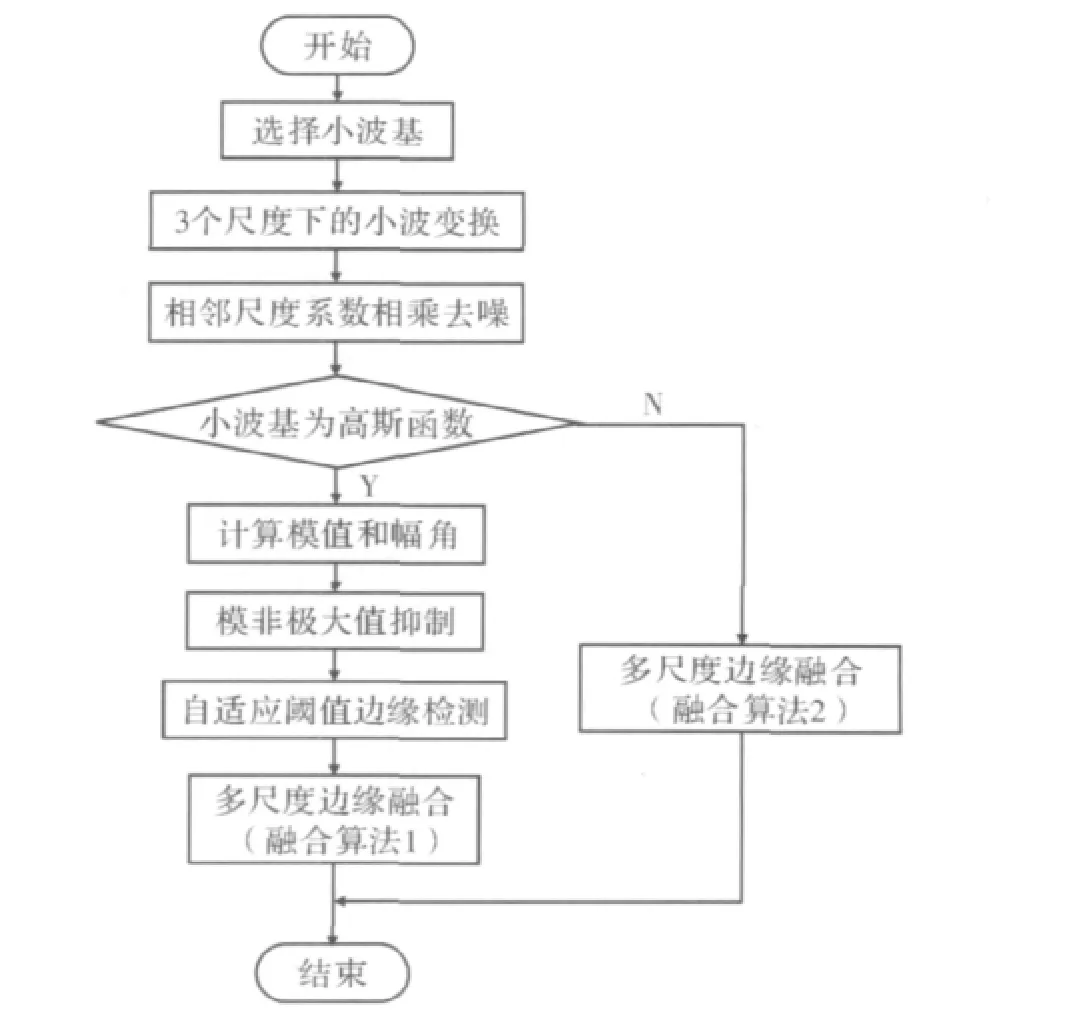
图1 算法流程图

2.2 算法的实现和结果分析

文中所使用的原始图片如图2所示。使用传统的Sobel、Prewitt、Canny和Log算子进行自动边缘检测，检测效果如图3所示;使用文中算法进行边缘检测效果如图4所示。对比图3和图4的检测效果，可以发现:Sobel和Prewitt算子进行边缘检测，虽然去除了超空泡的背景噪声，但只能检测到部分空泡边缘，弹丸的边缘几乎不能检测到;对于Canny和Log算子虽然能够提取更多的边缘信息，得到相对完整的超空泡边缘和部分弹丸边缘，但是边缘被淹没在背景噪声中。文中算法得到的边缘，能够去除大部分噪声，并且得到完整的超空泡外边缘和部分弹丸边缘。图4(a)和图4(b)相比，高斯小波基得到的超空泡外边缘连续性好，内部弹丸部分的边缘较少;B样条小波基得到的边缘相对完整，但边缘点的连续性相比图4(a)较差。

3 结束语

文中采用自适应多尺度小波边缘检测对超空泡图像进行边缘检测，算法中采用两种不同的小波基对超空泡图像进行多尺度的小波变换和相邻尺度边梯度增强，对得到的不同尺度下的梯度，采用K均值聚类进行边缘的自动分类，得到不同尺度下的边缘，并将不同尺度下的边缘进行融合，继而得到最终的边缘图像。

由于图像边缘是以人视觉直观感触为基础的，图像包含的信息千差万别，应用场景的不同也会导致对边缘的不同要求，因而并没有统一的量化指标可以作为边缘检测的评价依据[19]。从视觉的直观效果来看，文中算法得到的边缘，相比传统的边缘检测方法，有很好的抑制噪声效果，同时获得了更多的有效边缘信息，得到了很好的边缘检测效果，而且算法有较强的自适应性，在超空泡图像边缘检测的工程实现中，有较好的鲁棒性。

[1]连静，王珂，吕智莹.基于B样条小波的自适应阈值多尺度边缘检测[J].吉林大学学报:工学版，2009，35(5):542-546.

[2]王青竹，王珂，袁国良.多层次自适应空间系数高斯小波图像边缘检测[J].中国图象图形学报，2009，14(7):1348-1351.

[3]张志红，任杰.B样条小波边缘检测改进算法[J].四川兵工学报，2010，31(2):136-138.

[4]李牧，臧希，闫继宏.基于类内方差最小化及模糊控制算法的小波边缘检测技术[J].电子学报，2008，36(9):1741-1745.

[5]赵久梁，颜云辉，刘伟嵬.板带钢表面缺陷检测系统的多尺度边缘检测算法[J].东北大学学报:自然科学版，2010，31(3):432-435.

[6]翟艺书，柳晓鸣.基于小波变换和模糊c-均值聚类的图像边缘检测[J].大连海事大学学报，2005，31(4):83-86.

[7]黄凤贤，王保保.基于自动确定阈值的小波边缘检测技术研究[J].计算机仿真，2004，21(8):155-157.

[8]宋芬.多尺度边缘检测方法研究[D].湖南:中南大学，2008.

[9]郑子华，陈家祯，钟跃康.基于尺度间梯度方向的多尺度边缘融合[J].福建师范大学学报:自然科学版，2009，25(2):32-35.

[10]王雪松，宋凯.基于多尺度小波变换的边缘检测算法[J].沈阳理工大学学报，2008，27(4):16-19.

[11]王玮钊，李占贤，张进.基于小波变换的多尺度图像边缘检测算[J].河北理工大学学报:自然科学版，2009，31(3):88-90.

[12]郭显久.一种新的基于小波变换的边缘检测算法[J].大连水产学院学报，2005，20(2):158-162.

[13]王咏胜，付永庆.噪声目标的边缘检测算法研究[J].弹箭与制导学报，2008，28(6):235-237.

[14]王凯，于海勋，王广平.一种改进的小波多尺度相乘目标边缘提取方法[J].计算机仿真，2009，26(7):244-247.

[15]黄敏，姜静.基于相邻尺度小波变换乘积的镜头渐变检测[J].计算机工程，2010，36(3):195-196.

[16]岳思聪，赵荣椿，郑江滨.基于多尺度边缘响应函数的自适应阈值边缘检测算法[J].电子与信息学报，2008，34(4):957-960.

[17]陈书海，傅录祥.实用数字图像处理[M].北京:科学出版社，2005.

[18]MALLAT S G，ZHONG S.Characterization of signals from multiscale edge[J].IEEE Transaction on Pattern Analysis and Machine Intelligence，1992，14(7):710-732.

[19]祝强，徐瑾，张铎.小波模极大值边缘检测算法研究[J].武汉理工大学学报:信息与管理工程版，2008，30(6):849-853.