一种配电网络潮流计算的快速实用方法

杨秀菊 王晓波

1.山东省平原县电业公司 山东 平原 253100

2.吉林省电力有限公司 吉林 长春 130021

0 引言

电力系统潮流计算［1］是研究电力系统稳态运行情况的一种基本且重要的电气计算，是电力系统分析与控制学科领域的基础。潮流计算的任务是根据给定网络结构及运行条件，求出整个网络的运行状态，其中包括各母线的电压、网络中的功率分布以及功率损耗等。

潮流计算按电压等级主要分为输电系统潮流和配电系统潮流。输电系统潮流计算的研究经历漫长的研究历程，可以说目前已经相当成熟并得到广泛应用［2-3］，如牛顿法、基于牛顿法简化的PQ分解法被公认是最优秀的方法。然而，配电系统潮流计算的研究是上世纪80年代后开始的，近来由于配电自动化的逐步兴起使配电潮流计算的研究越来越显得特别重要。配电系统的特点是：电压等级低、电流数值大、传输损耗大等，从而配电元件的r/x比较输电元件要大，同时要求配电网应按环网设计（可靠、安全的要求）开环运行（防止电磁环）。配电网自身的特殊性使原有分析输电系统的算法难以直接应用［4］，由此，近年来电力工程界的学者们对配电系统潮流计算进行大量研究［5-6］，总体上分成两大类：一是根据KCL和KVL的递推算法；二是寻求同输电系统一样的统一算法。前者算法与网络结构有极强的关系使其在应用中缺乏灵活性；后者涉及算法收敛改进但在应用中具有较好的灵活性。本文依据后者的思想，根据前人的研究工作，由基本电工原理出发，导出配电网的潮流方程；根据配电网的特点，分析配电网潮流方程与网络拓朴的关系；根据系统运行的物理特点，简化配电网潮流修正方程中的雅可比矩阵，在充分利用放射网特点的基础上，给出基于牛顿法的配电网络潮流计算的简捷迭代格式。算例分析表明此方法有较好的适应性。

1 电网络的基本方程

对于一个线性、时不变RLC交流电路，基本的网络方程可表示如下：

由欧姆定律，网络支路电压与支路电流的关系为：

其中Yb网络支路导纳矩阵。

由KCL，节点注入电流与支路电流的关系为：

其中A为节点支路关联矩阵

由KVL独立闭合回路与支路电压的关系为：

其中B为回路支路关联矩阵 （见图1中示意的两个闭合回路）。

图1 放射状网络

同样道理，根据图1所示和式（3），支路电压与节点电压之间的关系可以表示为：

这样，由式（1）、式（2）和式（4）经简单推导可以得到：

其中AYbAT为节点导纳矩阵。对于放射状网络，经过一定的网络节点排序，节点支路关联阵 一定能表示成上三角或下三角的形式，这一特点对本文尤为重要。

2 牛顿法的特点

由于求解速度快和二次收敛等特点使牛顿法在解非线性方程组中得到广泛应用［7］。牛顿法是从某一初始点开始，通过对非线性方程组逐次线性化，进而求解修正线性方程组J·ΔX=Δb的过程。可见初始点的选取、系数矩阵J（也称为雅可比阵）的特性往往决定牛顿法是否有效。如下方程组：

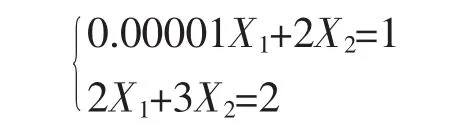
准确到小数点第九位的解为：X1=0.250001875，X2=0.499998749。若用四位浮点十进制数（仿机器实际运算），按高斯消去法求解，则有：

对发电机进行模态仿真分析，首先对发电机主要部件进行固有频率仿真分析，其次对发电机在使用刚度为10 kN/mm的弹性支撑下进行模态分析，最后对发电机在使用刚度为12 kN/mm的弹性支撑下进行模态分析。模态分析时轴承刚度输入条件如表2所示。

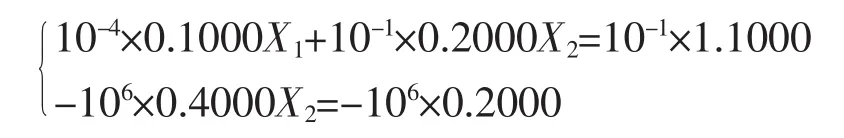
回代解得：X2=0.5000，X1=0，显然严重失真。造成这种结果的原因，就是小主元的出现，即方程组系数阵失去了对角优势。用小主元作除数引入了大的舍入误差，再经传播，误差变得更大。因此，对于牛顿法来说，不是所有问题都是普遍适应的。实践证明，对于输电系统的潮流计算，牛顿法及快速解耦法是一种行之有效的方法，但对于配电网却不然。由此，针对配电网，人们提出多种非牛顿类型的配电潮流计算方法，例如前推回推法。这种方法之所以很好的解决了配电网络中牛顿法所遇到的问题是因为它是基于网络理论的一种直接求解结构的方式，避开了求解修正方程的过程。然而，很难将这些方法灵活扩展到其他领域，例如状态估计、最优潮流等。因此，在配电网潮流计算中，寻求一种类似输电系统的统一潮流计算方法就显得特别重要。

针对牛顿法在配电潮流计算中遇到的问题，如果能有效解决雅克比矩阵的鲁棒性问题以及状态变量修正量的计算，得到同输电系统类似的潮流计算格式就不困难了，下节将集中阐述这个问题。

3 放射状配电网潮流计算的牛顿法

在牛顿法解潮流方法中，其修正方程可表示如下：

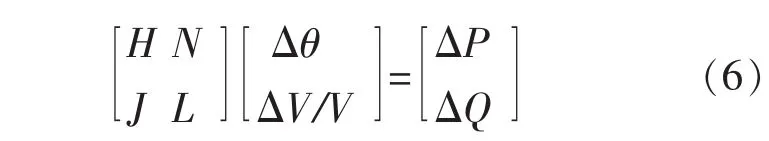
其中：Δθ，ΔV/V分别为节点电压的相角及幅值修正量的列向量，ΔP，ΔQ分别为节点注入有功、无功修正量的列向量，雅可比矩阵元素描述如下：

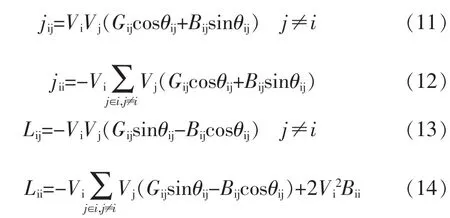
因为在配电网中，配电元件传输潮流不大，节点间的相位差很小，在修正方程中令sinθ=0；再假设并联支路用等值注入功率表示。在这种条件下，式（7）～（14）就可以简化为：

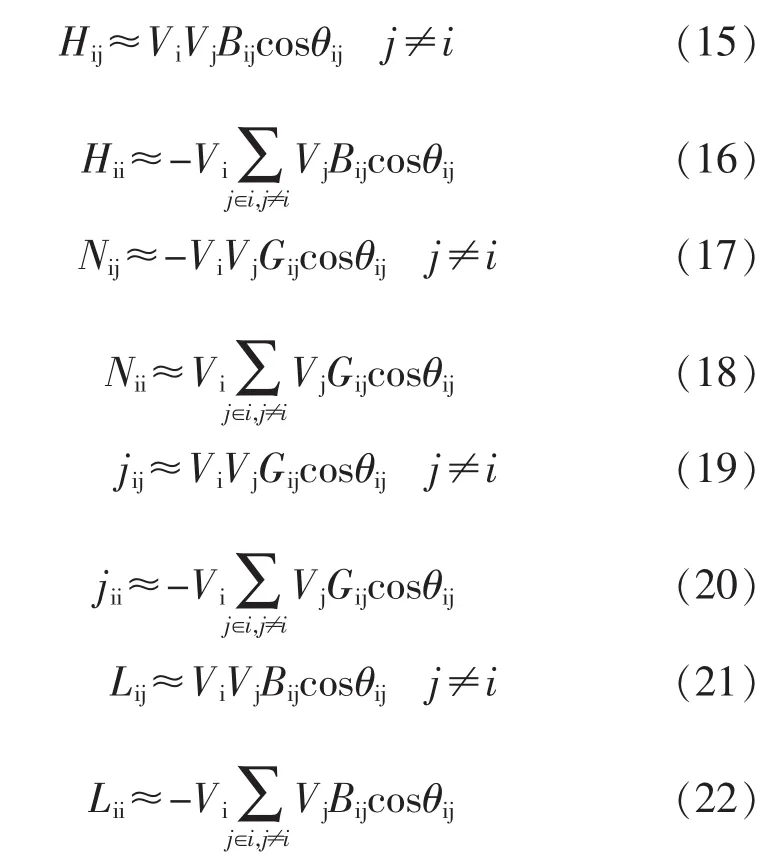
式（15）～（22）表明，矩阵 H、N、J和 L 和节点导纳矩阵一样都具有同样的性质（对称性，稀疏性）。因此可以得到：

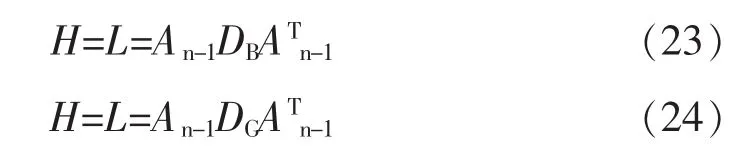
其中，DB和 DG为对角元分别为 ViVjBijcosθij和ViVjGijcosθij的对角矩阵。因此，（6）式可以被重新写为：

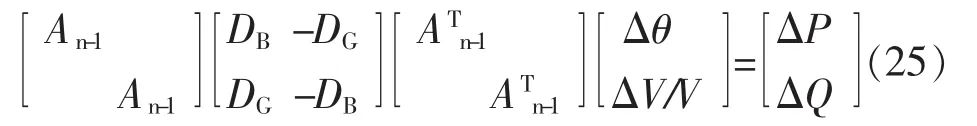
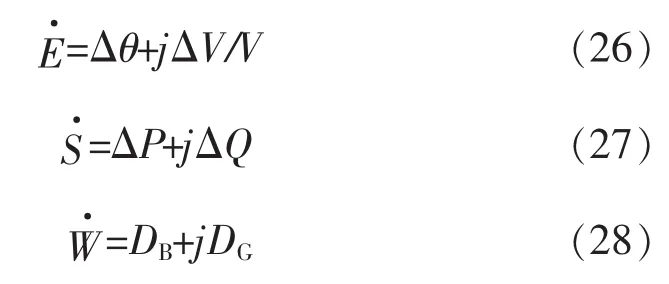
则式（25）可以写成：

注意，如果节点和支路被恰当地规定，An-1就是一个对角元为1而非对角元为-1的上三角矩阵。得到这样An-1的一种方法就是按照远离根节点（源总线）的层来规定支路。每个支路的方向都是指向根节点。规定支路的同时规定节点。支路的起始节点号同支路号相同，如图2所示。图2的节点支路关联式（30）。

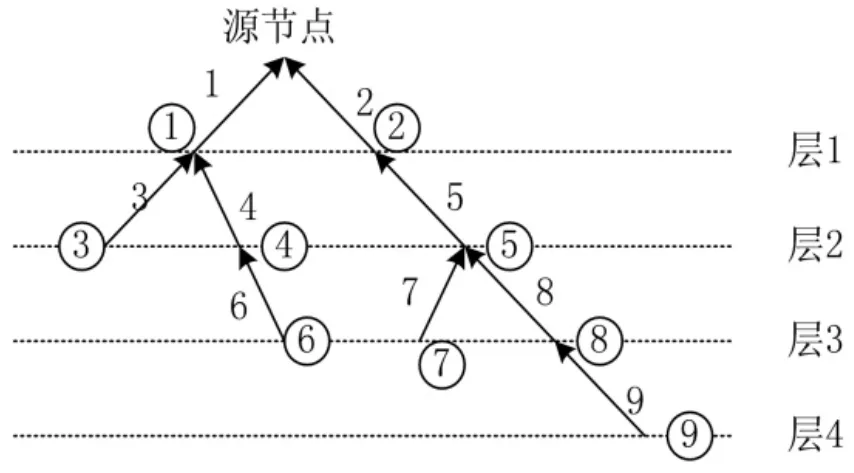
图2 一个简单的配电系统

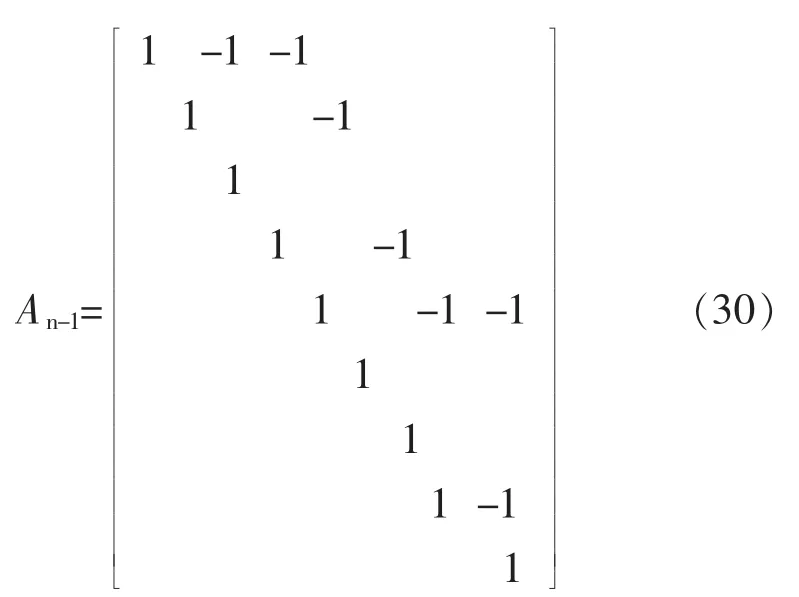
到这里，雅克比矩阵就以UDUT的形式出现，其中，U是一个由系统拓扑结构决定的连续上三角矩阵，D是一个分块对角矩阵。

再作变换：

这样，形成雅可比矩阵、LU分解的步骤可以被（31）、（32）直接的前代后代所代替。

由（29）式可以看出放射装配电网潮流计算的修正牛顿法是以这样的方式被推导出来的，在这种方式中，雅可比矩阵是以UDUT的形式出现，其中，U是一个由系统拓扑结构决定的连续上三角矩阵，D是一个分块对角矩阵。通过这种方法，传统的形成雅可比矩阵、LU分解的步骤可以被直接的前代后代所代替。这样，在计算过程中和雅可比矩阵以及它的LU因子有关的病态情况就可以避免。这一算法根源于传统牛顿法，人们多年来应用牛顿-拉夫逊法的经验可同样适用于配电网中。例如可进行潮流优化、状态估计等。

本文算法用C语言编写［8］，图3为算法的流程图。

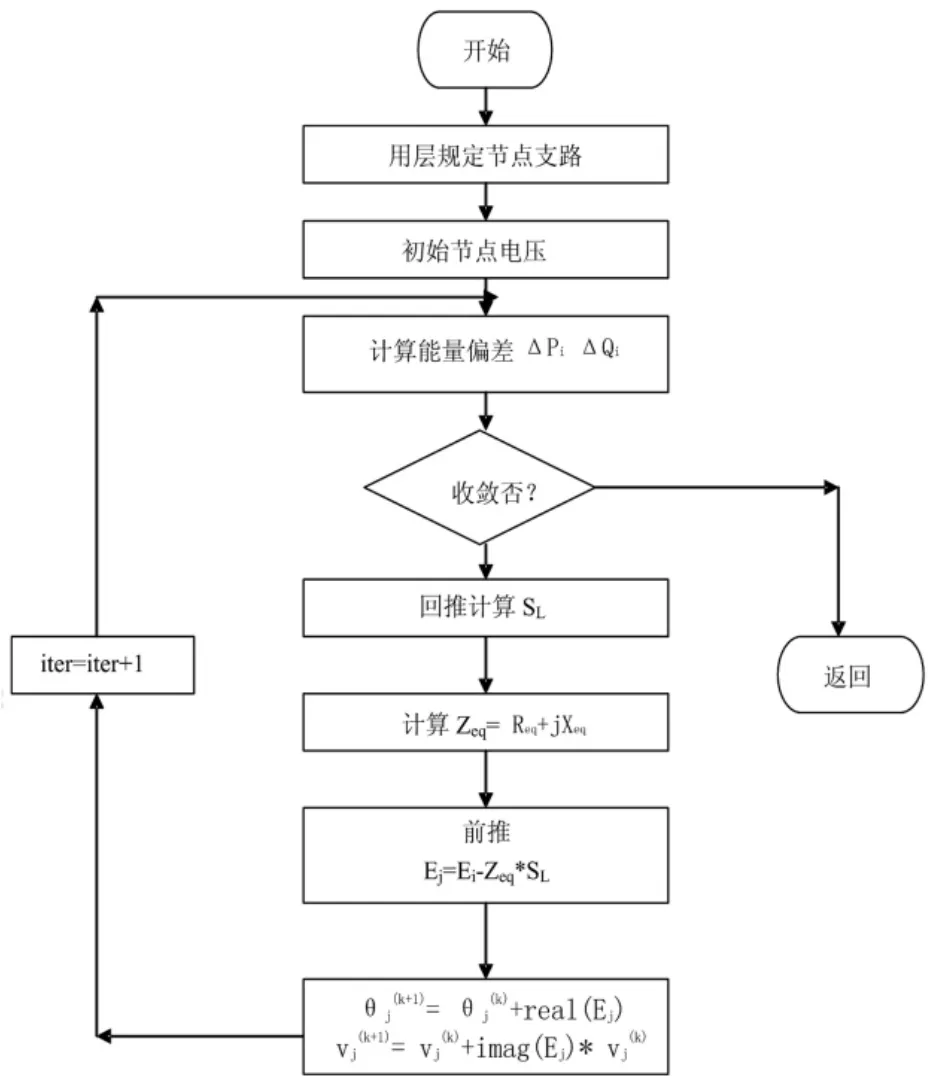
图3 改进牛顿法的流程图

4 算例

以九节点为例，同前推回推法作比较，如图9所示。

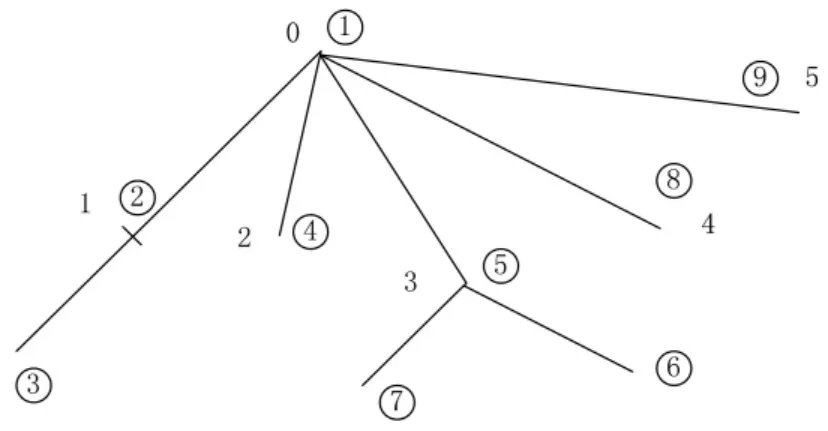
图4 9节点系统图

其中，0～8 为改进牛顿法对节点编号，①～⑨为前推回推对网络的编号。表1为系统参数：

表1 系统参数

算法的收敛判据为0.001，其中，改进的牛顿法迭代三次，前推回推法迭代一次，其结果比较如表2：

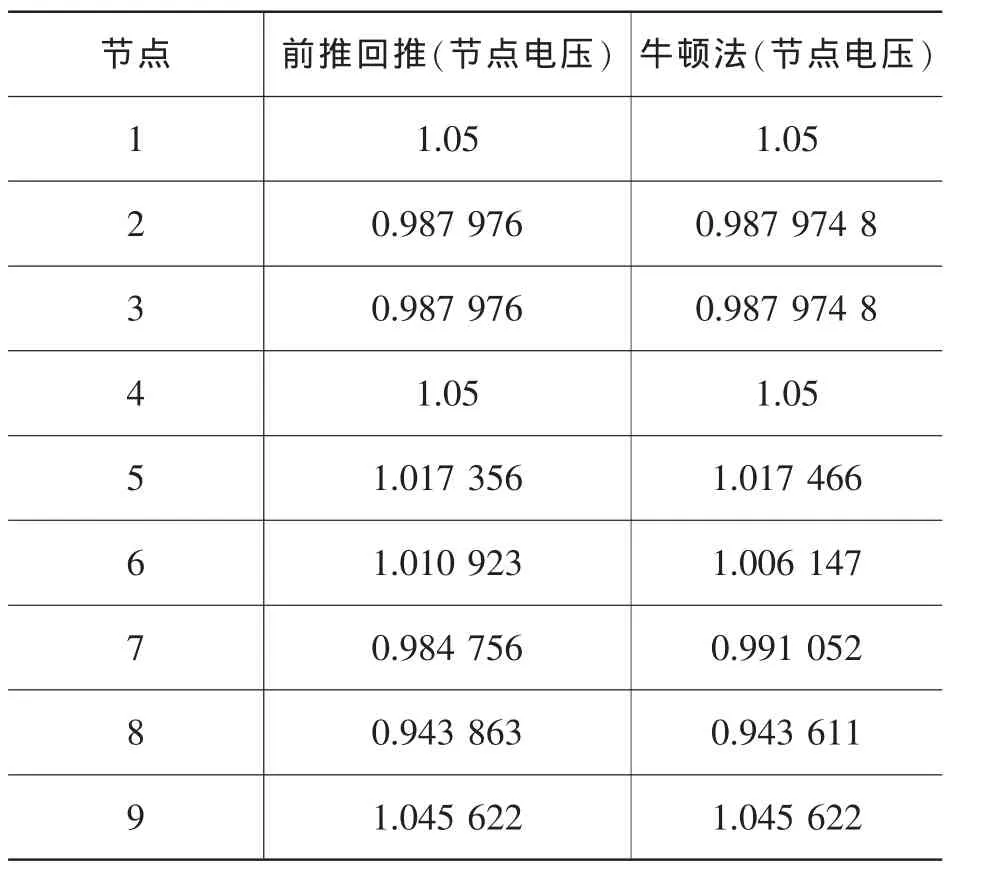
表2 计算结果

5 结论

本文阐述放射状配电网络潮流计算的牛顿法。推导表明，通过合理化简，放射状系统的雅可比矩阵可以成为UDUT的形式，并且这种形式和节点导纳矩阵具有同样的拓扑结构。这种结构自身构成修正方程前代回代的条件，免去因子分解的过程，增强了数值计算的稳定性，具有较好的应用前景和开发潜力。

［1］陈珩.电力系统稳态分析［M］.北京：水利电力出版社，1985.

［2］Zhang F，Cheng C S.A modified newton method for radial distribution system power analysis.IEEE Trans on Power Systems，1997，12（1）：389-397.

［3］Tinney W F，Hart C E.Power flow solution by newton's method.IEEE Trans on Power Apparatusand Systems，1976，PAS-86：1449-1460.

［4］Tripathy S C，Prasad G D，Malik O P，et al.Load flow solutions for ill-conditioned power systems by a newton like method.IEEE Trans on Power Apparatus and Systems，1982，PAS-101：3648-3657.

［5］李华东，韩学山，芦艺，张维国.配电网潮流计算的实用算法［J］.东北电力学院学报，1997，（01）.

［6］宋文南，李树鸿，张尧.电力系统潮流计算［M］.天津：天津大学出版社，1990.

［7］邓建中，葛仁杰，程正兴.计算方法［M］.西安：西安交通大学出版社，1985.

［8］谭浩强.C 程序设计［M］.北京：清华大学出版社，1999.