新型推力式流速传感器的测量原理与结构设计研究*

张小彦,秦建敏

(太原理工大学测控技术研究所,太原 030024)

在水文测验中,流速的测量是一个十分重要的项目。水文站在掌握水流速度的信息后可以间接得到河道断面的水流量。而水流量又是水库调度中的一个十分重要的参数,只有知道河道断面水流量才能知道流向下游的总水量,以满足下游用户对水的需求量,同时还能对下游的一些灾害起到预测的作用。另外,水流速度的测量对于研究水流的运动规律和水流泥沙的相互作用机理具有十分重要的意义,因而流速测量技术受到人们的高度重视。但是,在冬季结冰的情况下测量冰盖下的水流速存在困难,首先环境温度较低一般在零下二十度左右,另外冰下水中含有冰花,而且冰下测流专用仪器很少,无论在国内还是国外几乎为空白。

鉴于此种情况本文提出一种通过流体水平推力来测量冰下含冰花水流速的传感器及其检测方法,为解决冰水情监测中冰下含冰花的水流速测量提供一种新的技术手段。

1 流速检测基本原理

通过颗粒相的特性实现对流速的自动检测是一种新的检测方法,该检测方法是基于两相流动力学中颗粒相特性中的流体作用于刚性球体上的阻力理论来对流体流速进行检测的。流体绕球流动时,球体受到的流体推力和流体流速之间有个经验公式,利用此经验公式可以实现对流体流速的检测。

假设来流是完全均匀的,则球体在静止流体中运动所受的阻力和运动着的流体绕球流动作用于静止球体上的推力是相等的。在下面的论述中,对这两种情况不作严格区分。

球体在粘性流体中运动时,流体作用于球体上的阻力 Fd由压差阻力和摩擦阻力组成。阻力 Fd的表达式如下：

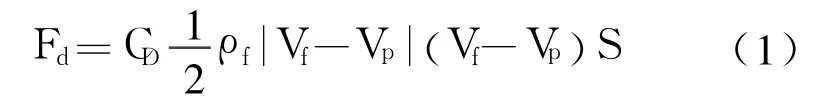
式(1)中 Vf和 ρf是流体的速度和密度;Vp是球体的速度;S是球体的迎风面积,其中 S=πrp2(rp是球体半径);CD是阻力系数。该式考虑了球体与流体间的相对运动,阻力 Fd的方向与(Vf-Vp)的方向一致[1]。

目前,阻力系数 CD主要依靠实验来确定,实验中阻力系数 CD和雷诺数 Re有关。

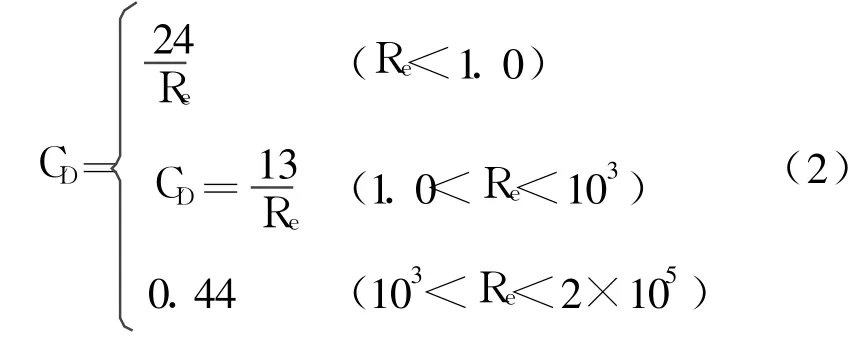
按照流速传感器实验装置的实验条件计算的雷诺数 Re满足：5×103＜Re＜1.5×105,所以检测流速时阻力系数 CD取 0.44,此时流体作用于球体上的力 Fd表达式如下所示：

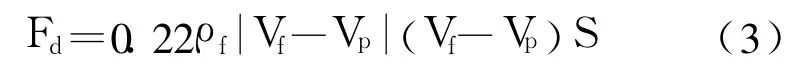
设球体的半径为 r,水的密度为 ρ,水流速度为Vf,球体静止,此时水对球体产生的力是推力 Ft。

按照公式(3)计算

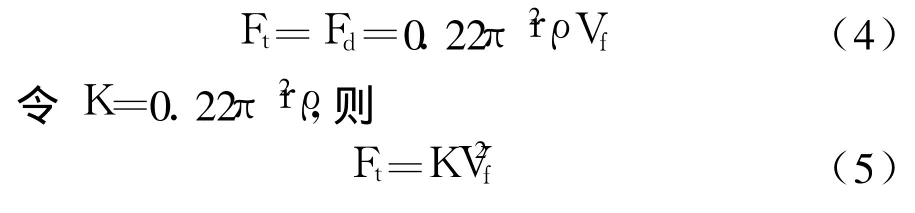
根据上面的推导可以得到运动着的流体绕球流动时,作用于静止球体上的推力 Ft和流体流速 Vf之间的经验公式(5)。

2 新型推力式流速传感器的结构

结合上述两相流动力学中流体绕球流动时流体对刚性球体的推力 Ft和流体流速 Vf之间的经验公式我们设计了该推力式流速传感器实验装置,其测量结构框图如图 1所示。

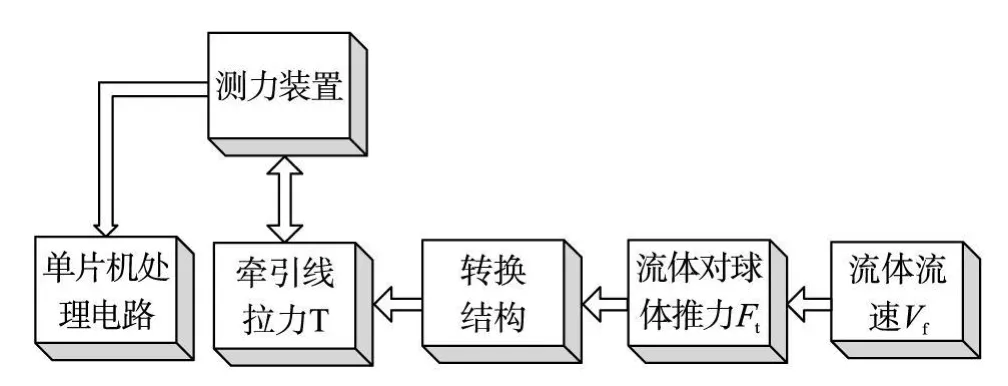
图1 流速传感器结构框图

由经验公式(5)可知,若已知推力 Ft的情况下就可以得到流体流速 Vf的值,但是对此推力 Ft直接测量存在较大的困难。从图 1中可以看出该流速传感器实验装置通过转化结构将对此推力 Ft的测量转化为对牵引线拉力 T的测量。本测量结构采用了精密弹簧和位移检测结构组成的测力装置来测量牵引线拉力 T。流速的测量过程中牵引线上产生的拉力 T的范围在 1 N以内,应用 TH 4802-Ⅰ型称重传感器也可以直接测量此拉力 T,但此种测量结构在本论文中未讨论。测力装置将测得的数据传给单片机处理电路处理最终得到流体流速 Vf。通过测量牵引线拉力 T间接得到流体对球体的推力 Ft进而实现对流体流速 Vf的测量使得测量难度降低。

基于流速测量的基本原理和流速传感器结构框图(1),我们设计了新型流速传感器的实验装置。该实验装置由敏感部件、转换结构、位移检测结构三部分组成,结构如图 2所示。

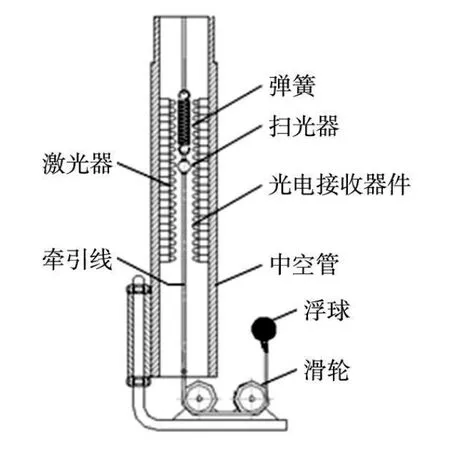
图2 流速传感器实验装置的结构示意图

图2中浮球是传感器的敏感部件,该浮球将水对浮球的推力 Ft与水流速 Vf联系起来,同时通过对浮球受力分析将推力 Ft和拉力 T联系起来。在水流稳定时对水中处于平衡状态的刚性浮球受力分析我们总能得到浮球自身的重力 G、水对浮球的浮力 Ff1、牵引线对浮球产生的拉力 T、水对浮球的推力 Ft四个力。浮球受力情况如图 3所示;建立 X、Y轴进行正交分解如图 4所示。

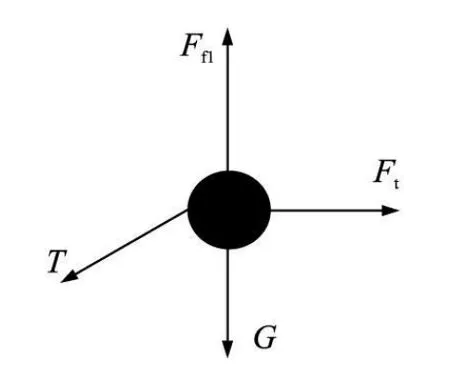
图3 浮球受力图

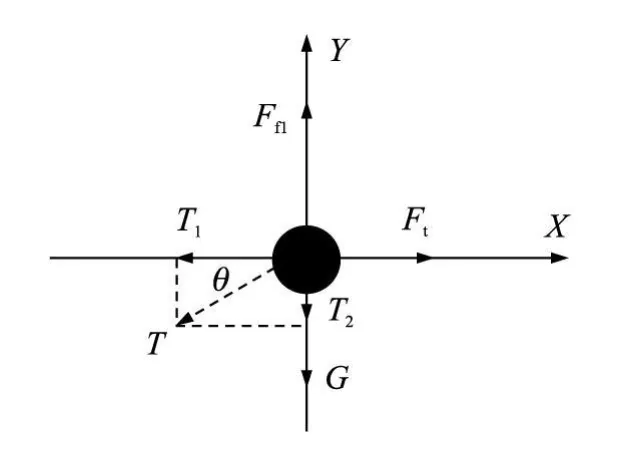
图4 正交分解图

经正交分解建立平衡方程如下：

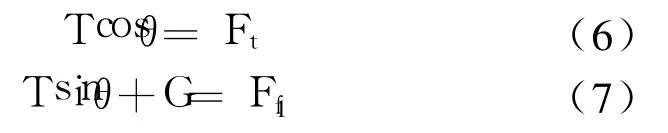
由式(6)、式 (7)计算得

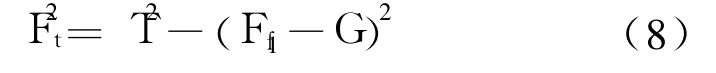
结合

得到

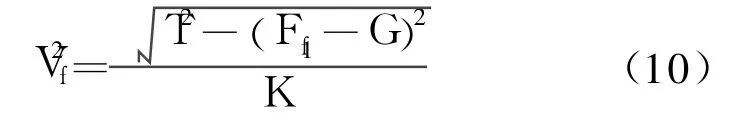
根据阿基米德原理

又因为

将式(11)、式(12)代入式(10)得到流体流速计算公式

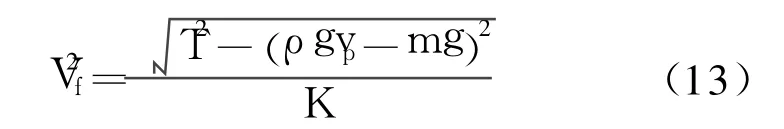
式(13)中 K在实验条件确定情况下为已知,其中 ρ、vp、m均为已知,从而通过测量拉力 T就可以得到水流速 Vf。上面的受力分析具有任意性因此能够适应流速变化的情况。

由于水对浮球的推力 Ft难以直接测量,因此通过转化结构将对推力 Ft的测量转化成对牵引线拉力 T的测量。传感器中的转换结构由弹簧、牵引线组成。牵引线的拉力 T可以利用胡克定律通过位移检测结构来测量。由于牵引线拉力 T很小所以要求位移检测装置为非接触式的,另外,由于考虑到位移检测装置的安装条件,我们将激光器、光电接受器件、挡光器、单片机处理电路组成位移检测结构。一列激光器等间距固定在中空管内壁上,一列光电接受器件等间距固定在和激光器成 180°位置的中空管内壁上。一列光电接受器件接受相对应激光器发射的激光,光电接受器件将输出的 TTL电平传给单片机控制电路处理。光电接受器的间距为0.5 cm,弹簧的形变量范围为 25～100 cm因此虽然位移检测装置的分辨率不高但是相对于弹簧的形变量范围和测量要求来说能够满足要求。弹簧下端的挡光器挡住某个光电接受器件时,光电接受器件输出的 TTL电平就会翻转,单片机处理电路就会得出哪个光电接受器件被挡住了,由于光电接受器件等间距排列,从而可以得到弹簧的形变量,单片机处理电路会进一步利用胡克定律得到牵引线对浮球所产生的拉力 T。因此,再利用式(13)中 Vf和 T的关系就可以得到水流速 Vf。

3 流速传感器实际应用及数据分析

2009年 12月下旬到 2010年3月下旬作者将流速传感器实验装置在黄河内蒙段的河道上进行了测试原理功能验证实验。具体位置在呼和浩特辖区的托克托县境内的一个黄河水文监测站头道拐水文站。实验时,首先将冰盖层面凿开一个直径大于流速传感器直径的洞,然后将传感器实验装置从这个大洞垂直插入冰花层中,要保证传感器下端处于冰盖层下面的冰花层中,传感器上端应保证至少有三分之一暴露在冰面上。通过实验,取得了大量的原始数据。在所测的大量流速实验数据中,抽出 5组原始数据如下：

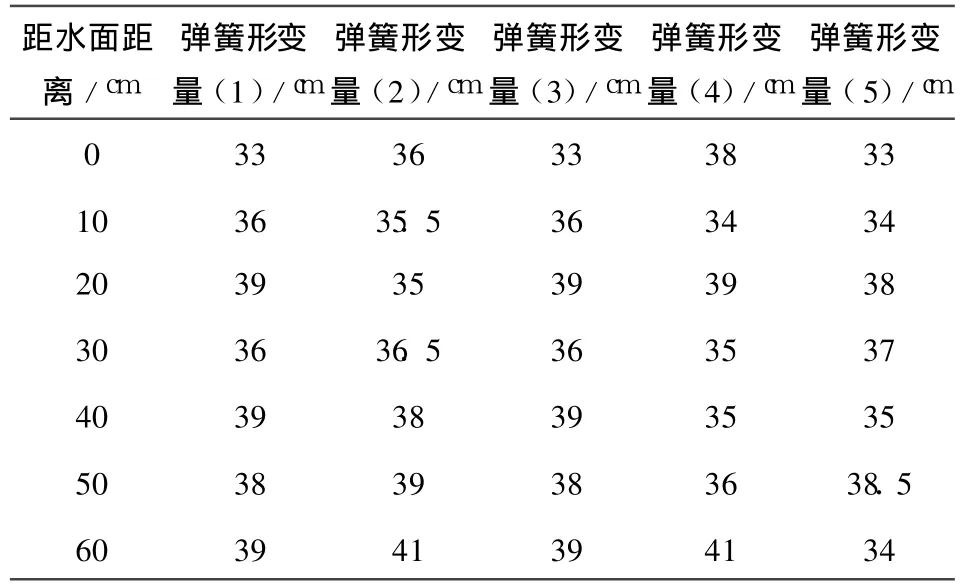
表1 黄河河道断面垂直方向上不同水深时采集到的弹簧形变量

将表 1中的弹簧形变量利用胡克定律计算可得到牵引线拉力 T,然后将 T代入公式(13)即可以得到水流速 Vf。将抽出的5组数据经过进一步计算得到水深和水流速关系,绘制成曲线如图 5所示。

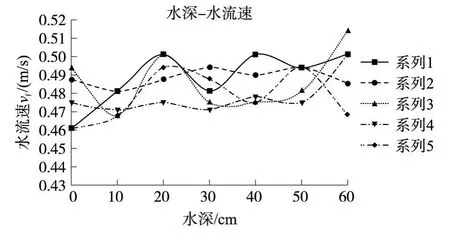
图5 黄河河道断面垂直方向水深和水流速测试数据曲线

由于实验现场处于黄河河道拐弯处,河道地形及河水流场分布复杂,所以得到的曲线有多次振荡,与实际的垂直断面上流速的分布有些不符。但是,从图表上我们仍可以直观的看出不同水深处的流速是不同的。由于各组流速测试值不是同步完成的,因此,该图还反映了河道断面同一个位置上不同时刻的流速变化情况。

4 结束语

由于目前没有实际可用的冰花水层流速测量设备,上述实测数据无法通过其它检测设备的测试结果进行对比验证,仅仅是对这一新型流速传感器功能的实际验证。对于冰花多少对浮球受到的浮力的影响,采用弹簧后测试过程中由于其变形与反复伸缩引起的测量误差,以及采用光电方法检测位移影响仪器的精度等问题在本文中尚未考虑,这些问题将留待今后的研究中加以解决,但从实验数据可以看出,新的推力式流速传感器检测原理是可行的。

从力学角度出发实现对水流速的自动检测,是一种新的流速检测方法。而且,这种方法不仅可以实现对水表面流速的测量,还可以实现对冰盖下水流速的测量。该流速传感器结构简单,成本低。通过以上分析,结合作者采用新型流速传感器实验装置所做的大量基础实验,利用这种方法测水流速是可行的。

[1]方丁酉.两相流动力学[M].北京：国防科技大学出版社,1988：42-51.

[2]蔡守允.河流海岸模型测试技术[M].南京：南京水利科学研究院专著出版基金资助,2004：30-47.

[3]文华,朱玉琛,付广.流速仪在国内外的研究现状[J].舰船防化,2007(3)：43-45.

[4]马志敏,李强,刘爱东,等.热阻式流速仪的设计[J].传感器技术,2005,24(7)：49-51.

[5]秦平,陈鲁疆,王沛云.一种新型便携式旋桨流速仪[J].海洋技术,2009,28(1)：37-40.

[6]双正文,茹纯亮,吕霞付.基于嵌入式的智能流速仪研制[J].2008(12)：70-75.

[7]蔡守允,谢瑞,韩世进,等.多功能智能流速仪[J].海洋工程,2004,22(2)：83-86.

[8]蒋佑华,林晓明,黄茂华,等.电波流速仪测流应用及精度分析[J].水利水文自动化,2003(4)：39-42.

[9]周建炯.智能流速仪的研制[J].浙江水利科技,2003(3)：63-64.

[10]杨中华.黄河冰凌灾害遥感动态监测模式及冰情信息提取模型研究[D]：[博士学位论文].北京：中国地质大学,2006：22-23.

[11]Neuhaus M,Looser H,Burtschcer H,et al.Flow Meter for High-Purity and Aggressive Liquids[J].Sensors and Actuators A：Physical,2007,134(2)：303-309.

[12]Temperley Neil C,Masud Behnia,Collings Anthony F.Application of Computational Fluid Dynamics and Laser Doppler Velocimetry to Liquid Ultrasonic Flow Meter Design[J].Flow Measurement and Instrumentation,2004,15(3)：155-165.