车体结构多目标拓扑优化设计探讨*
2011-05-04沈安林肖守讷
沈安林,肖守讷
(西南交通大学 牵引动力国家重点实验室,四川成都,610031)
车体结构设计初期(概念设计阶段)找出最佳的材料分布是极其重要的,与参数优化、形状优化相比,拓扑优化从产品设计之初就开始优化,其优化空间更大,拓扑优化后的概念模型,再经过形状优化、参数优化后,其结构性能可较大地提高[1,2];目前,连续体的拓扑优化主要集中在单目标的拓扑优化,但车体结构作为车辆的承载基体,既需要满足多种静态工况下的性能要求,又要满足车体结构动态工况下的性能要求:如一阶垂向弯曲频率、一阶扭转频率,因此,车体结构的拓扑优化是一个多目标拓扑优化问题;连续体结构拓扑优化目前比较成熟的有均匀化方法(Homogenization Method)和变密度方法(Artificial Materials)[3,4],均匀化法的设计变量较多,但鉴于工程实际问题的复杂性,常用于拓扑优化的理论研究,而变密度法仅以单元密度作为变量,较为广泛用于工程实际;工程中常将多目标优化问题通过线性加权处理方法转化为单目标问题[5,6]:如利用层次分析法(AHP法)实现电动车身的多刚度拓扑优化[7],采用折衷规划法与平均频率法实现车架的拓扑优化[8];采用应变能指标函数将车体结构静态多目标与动态多目标结合起来实现车体结构静动态组合拓扑优化,通过多次迭代计算,得到清晰的车体结构和合理的传力路径,从而为车体结构设计提供思路。
1 多目标拓扑优化
1.1 多目标优化问题数学模型
多目标问题的数学模型如式(1)所示,处理这类问题有约束法、分层序列法以及评价函数法,而线性加权法由于方法简单易行,计算量小,常为工程实际所采用[9]。通过线性加权,多目标问题则转化为新的目标函数其中加权系数 ωi≥0(i=1,2,…,p)且

式中minF(x)表示求总目标函数F(x)的最小值,x=(x1,x2,…,xn)T,p ≥2,f1(x),f2(x),…,fp(x)分别表示各子目标的目标函数;s.t为“满足于的”缩写,以下类同;gi(x)表示约束函数。
1.2 静态工况的目标函数
在静态单工况下,为了得到结构最大的承载能力,常采用载荷作用下结构的应变能(柔度)作为目标函数,结构设计域体积分数(体积)或质量分数(质量)作为约束条件,而设计变量为单元的密度,静态工况优化模型如式(2)所示。

其中x=(x1,x2,…,xn)T,n≥2。其中 x为设计变量(伪密度);C(x)为目标函数(结构应变能函数);F为节点载荷向量;U(x)为节点位移向量;V(x)为优化后结构的有效体积;V0为结构的原始体积;f为体积约束的百分比;n为设计变量的数目。静态多工况情况下,对各子工况的响应进行加权求和,则目标函数变化为:minC(x)= ∑ωkCk(x),其中 ωk为第k个子工况的加权系数,各工况的权值可根据其重要程度而选取,Ck(x)为第k个子工况对应的应变能。
1.3 动态工况的目标函数
针对频率的动力特性拓扑优化目标函数是在满足结构约束的情况下改善结构的频率特性,即改善结构的模态特性,使结构刚度、质量和阻尼特性得到优化配置,达到结构减振降噪的目的。无阻尼自由振动模型的特征值问题如式(3)所示。
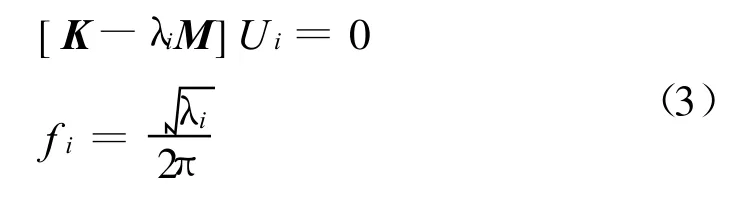
式中K是结构的刚度矩阵;M是质量矩阵;λi和Ui为特征值和特征向量;fi为固有频率。频率特征优化的数学模型如式(4)所示。

其中:x=(x1,x2,…,xn)T,n≥2,wj为第j阶特征值倒数的加权系数。
1.4 静动态工况总目标函数
采用权系数方法,目标函数间必须有相同的度量单位,即有相同的数量级,但车体结构应变能与频率之间的数量级之间存在较大差异[10],如果不引用一个值来平衡两者之间的差异,则计算结果将受数量级高的目标所支配,一般来说,结构的应变能数量级在1.0×104~1.0×106之间,而结果特征值倒数的数量级为1.0×10-5,因此,为了平衡二者数量级之间的差异,常引入一个平衡因子NORM,NORM=Cmax◦λmin,Cmax是所有子工况中最大应变能值;λmin是最小的特征值。wj为第j阶特征值倒数的加权系数。因此,车体结构进行静态工况和动态工况联合拓扑优化,其应变能组合指标函数(静动态工况总目标函数)可以写成式(5)。

2 车体结构多目标拓扑优化
2.1 车体结构优化模型
车体结构由底架、侧墙、车顶、端墙等几大部件组成,为了充分挖掘拓扑区域的可能结构形式,除车门,车窗及端门开孔外,其他结构均封闭;同时对设计域进行三维网格划分,因四面体单元和六面体单元对拓扑优化影响不大,为便于网格划分,车体结构全部采用四面体单元,如图 1、图 2所示,有限元模型中节点数为249 795,单元数为837 767,约束施加于二系弹簧位置,垂向载荷以重力加速度的方式施加在结构上,拉伸压缩力通过载荷等效原理施加在相应位置的节点上。因为在车体结构设计校核中,压缩工况、车钩拉伸工况、上弦梁压缩工况与其他工况相比,其设计条件更为恶劣,所以本例中仅考虑车体结构中较为重要的3个工况:车钩压缩工况、车钩拉伸工况、上弦梁压缩工况。优化模型选用单元密度作为设计变量,组合应变能指标函数作为目标函数,约束条件则选用设计域的体积分数。

图1 车体拓扑优化设计域有限元模型

图2 车体拓扑优化设计域有限元模型(局部)
2.2 车体结构优化结果
经过多次迭代,过滤掉底密度单元,车体结构各大部件优化后的结构形式如图3~图6所示,组合应变能指标函数迭代历程如图7所示,设计域的组合应变能由原来的3.32×107降低到0.61×107,而结构前3阶频率均有明显的提高,前3阶响应频率迭代历程曲线如图8所示。从图7及图8的优化结果来看,组合应变能指标函数与底阶频率响应趋势相反。
3 拓扑优化结果分析

图3 车体底架拓扑优化结果

图4 车体侧墙拓扑 优化结果

图5 车体顶盖拓扑优化结果

图6 车体端墙拓扑 优化结果

图7 组合应变能指标函数迭代历程曲线
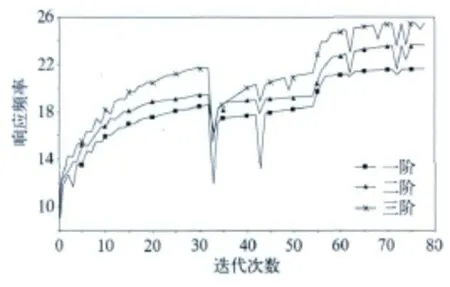
图8 低阶频率迭代历程曲线
对于纵向压缩,力流主要通过牵引端传递到边梁上,形成一个叉形结构,如图3所示,而底架中部优化的结果近似为一个桁架结构,有利于底架结构的稳定,同时,底架端部通过端墙连接将力传递到车顶上,如图6所示,因侧墙两端开有门,力流终止,只能通过车顶与侧墙之间进行传递,从而使车体各部件之间形成一个承载整体;对于纵向拉伸,其力流传递路径与纵向压缩基本一致;对于上弦梁压缩,力流主要通过两悬梁进行传递,同时也通过端墙将力传递到底架;从上面的分析可以看出,端墙结构在整车结构设计中相当重要,它能实现底架与车顶间力的传递;同时,从拓扑优化结果图4、图5来看,侧墙的中部结构和车顶的中部结构对车体的低阶频率影响较大。
通常为便于车体加工制造,梁的布置常采用横平竖直的结构,但从拓扑优化结果来看,平常所采用的横平竖直结构对车体整车承载能力贡献较低,而采用三角形结构或者桁架结构能使车体结构性能有明显的提高,有利于提高结构的稳定性和整车的刚度;从端墙拓扑优化结果来看,梁斜着布置有利于力的传递,因此,车体结构设计中,在一些允许区域,应参考拓扑优化结果确定梁布置的方向及确定梁截面的大小;同时,利用拓扑优化结果里面的孔洞结构,为车辆穿孔布线、空调设备等的安装位置提供依据。
4 结束语
应用组合应变能指数函数实现了车体结构的多目标拓扑优化,将车体结构静态多目标拓扑优化与动态频率多目标拓扑优化同时考虑,并参考某型车体外形尺寸及其特点,建立了车体结构的有限元模型,确定了车体结构设计域及设计载荷,通过该方法,完成了车体结构静动态多目标拓扑优化,拓扑优化后得到的车体结构清晰,各部件力流传递路径明显,为车体各部件下一步的详细设计提供思路和参考依据。
[1] 李 芳,凌道盛.工程结构优化设计发展综述[J].工程设计学报,2002,9(5):229-235.
[2] 周克民,李俊峰,李 霞.结构拓扑优化研究方法综述[J].力学进展,2005,35(1):69-76.
[3] Hans A Eschenauer,Niels Olhoff.Topology optimization of continuum structures[J].Appl Mech Rev 2001,54(4):330-390.
[4] B.Hassani,E.Hinton.A review of homogenization and topology optimization I-homogenization theory for media with periodic structure[J].Computers&Structures,1998,69:707-717.
[5] T.Y.Chen,S.C.Wu.M ultiobjective optimal topology design of structures[J].Computational Mechanics 1998,21:483-492.
[6] Seungjae Min,Shinji Nishiwaki,Noboru Kikuchi.Unified topology design of static and vibrating structures using multiobjective optimization[J].Computers&Structures,2000,75:93-116.
[7] 扶原放,金达锋,乔蔚炜.多工况下微型电动车车身结构拓扑优化设计[J].机械设计,2010,27(2):76-80.
[8] 范文杰,范子杰,苏瑞意.汽车车架结构多目标拓扑优化方法研究[J].中国机械工程 ,2008,19(12):1 505-1 508.
[9] 唐焕文,秦学志.实用最优化方法[M].大连:大连理工大学出版社,2004.
[10] 张胜兰,郑冬黎,郝 琪,等.基于Hyperworks的结构优化设计技术[M].北京:机械工业出版社,2007.
