温差作用下磁浮轨道梁变形分析及比较

顾 芸，滕念管

(上海交通大学 土木工程系，上海 200240)

磁浮轨道交通系统是一种高速无接触的系统，规范和实际工程对于轨道梁不平顺幅度、挠度及振动变形有非常严格的要求和限制。现有规定提出的满足运营安全和舒适度要求的温度设计参数为上下温差引起的挠度，应≤梁长的1/6 500。然而在实际工程中，这个标准很难达到。是这个规定过于严格，还是现有的轨道梁没有满足安全储备引起了人们的关注。

1 磁浮轨道梁温度荷载稳态分析

目前对轨道梁进行温度分析时大多数采用瞬态分析方法，主要是考虑自然环境中复杂的热交换过程，例如太阳辐射、结构物所在方位等不确定因素。然而正是因为热荷载的不确定性，使得瞬态分析的结论很难考虑到最不利的情况，得出的结论很难具有普遍性。

针对这个问题，对磁浮轨道梁的温度分析提出稳态分析方法。根据现有规定，对磁浮施加温差荷载60℃，研究在不随时间变化的温差极限荷载作用下磁浮轨道梁的温度变形，判断其是否满足现有规定，并对规定提出建议。

1.1 理论依据

根据Fourier热传导理论，无内热源和瞬态温度场的二维度导热微分方程为

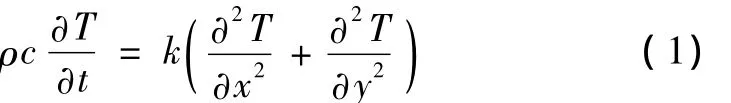
其中，k为导热系数;ρ为箱梁混凝土密度;c为混凝土比热容。

1.2 热荷载和边界条件类型

参照现有对磁浮轨道梁温度变形的规定，对异形截面混凝土箱梁结构施加两种温度荷载:温差荷载和对流换热荷载，并以初始条件的形式施加在建立的三维实体模型上。其中温差荷载属于第一类边界条件，对流换热荷载属于第三类边界条件。

1.2.1 温差荷载的施加

针对不同的环境温度，对梁顶面施加温度荷载，并确保梁顶面和底面的温度差值为60℃。例如，环境温度为30℃，为了保证上下表面的温差为60℃，顶面添加90℃的温度边界条件，并根据计算所得到的底面温度的结果对顶面温度进行调整，以满足温度差值的要求。本文设定三个常见的环境温度:10℃，20℃和30℃。

1.2.2 周围环境影响

为了模拟不同环境对温差作用下的轨道梁的影响，施加对流换热荷载及长波热辐射荷载。梁边界与周围流体间的传热系数h为对流换热系数和等效长波热辐射系数之和。

对流换热系数:对流热交换系数主要取决于风速、表面粗糙程度、表面法线方向以及材料类型，可由试验确定或按经验公式计算。国内外有关文献中对对流换热系数的取值规定差异较大，一般可按表面位置不同分别表示为:

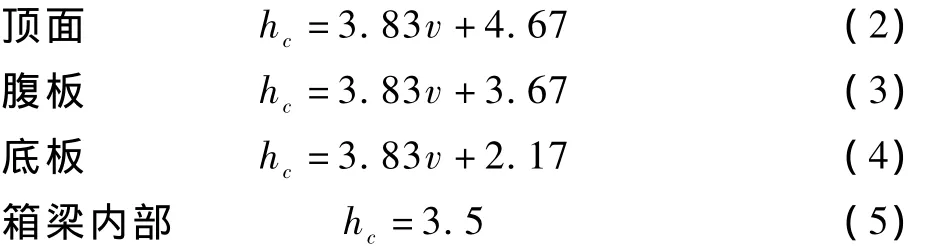
式中，风速v取为1 m/s，可以得到异形截面预应力混凝土箱梁各边界的对流换热系数。

长波热辐射换热系数可近似表示为:

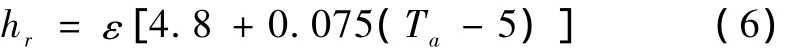
式中，ε为混凝土表面黑度系数(0≤ε≤1)取值为0.88;Ta为周围大气温度(℃)。

2 计算模型简介

以上海磁浮轨道梁为工程背景，选择现在运行的轨道梁以及两种备选梁的跨度和截面(图1)，比较其在不同气温环境，温差荷载作用后的温度场分布和位移。利用ANSYS有限元中的solid 5三维热-结构耦合单元计算(图2)，得到温度分布和轨道梁的位移。为了模拟不同环境温度下同等温差作用的温度效应，本文取常见的三种气温环境:10℃、20℃、30℃的气温，并保证上下梁表面温度差值为60℃的轨道梁模型进行分析计算。梁的参数选择为:导热系数取2.34 W/(m·K)，比热容取 1 046 J(kg·K)，密度取 2 500 kg/m3。

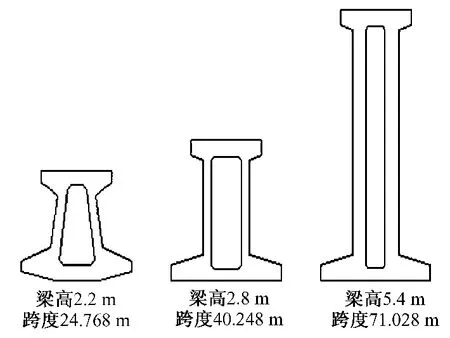
图1 3种不同的截面和跨度

3 计算结果及比较

3.1 温度场分布分析

图2 三维模型

在温度荷载作用下，磁浮轨道梁的最大挠度出现在跨中。从ANSYS后处理选项选取跨中的截面，可以得到每个节点的温度值。对其同一高度的节点温度值取平均值，得到沿高度方向分布的温度值。梁高2.2 m轨道梁的温度分布见图3。

对跨度40.248 m截面高度2.8 m的轨道梁和跨度71.208 m截面高度5.4 m的轨道梁做了温度场分析，见图4和图5。

由图3可以看出，在不同的环境温度、同样的温差荷载下，轨道梁温度分布呈现比较规律的曲线形式，说明计算模型和计算方法比较稳定可靠。在温差荷载作用下，轨道梁温度沿高度的增加而逐渐增加。增加的幅度有所不同。对三个模型的温度分布数据作比较分析，可以总结出基本的规律如下:在轨道梁截面底部一段区域内，温度和环境温度保持一致，没有温差变化。在距离顶部1.5 m附近，温度开始增加，且幅度越来越大。在距离顶部1.0～1.5 m之间，温度增加1℃。在距离顶部0.37～1.00 m之间，温度增加20℃。在距离顶部0～0.37 m之间，温度增加40℃。

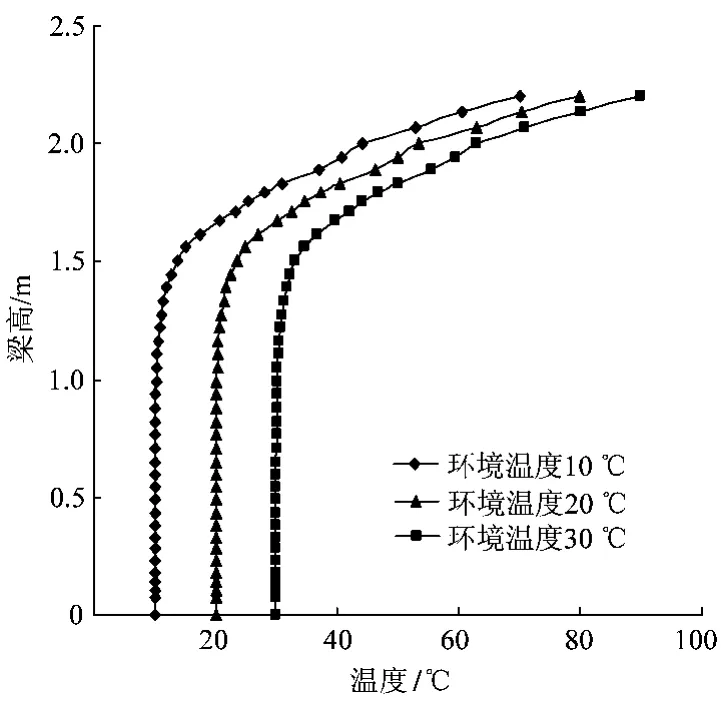
图3 梁高2.2 m温度沿高度分布

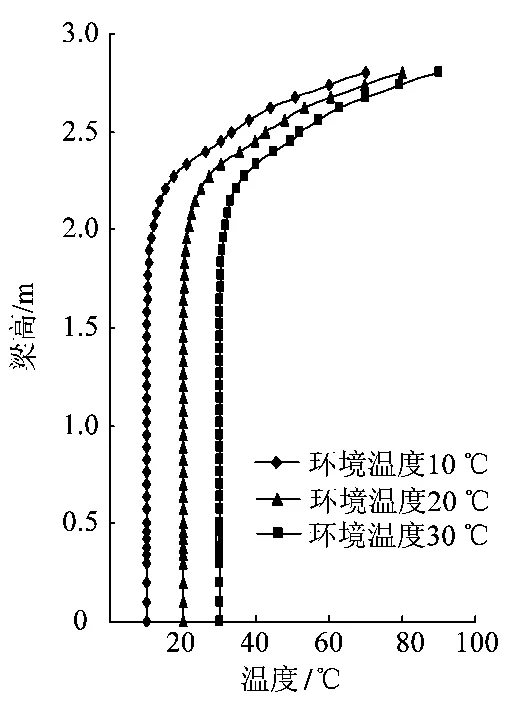
图4 梁高2.8 m温度沿高度分布

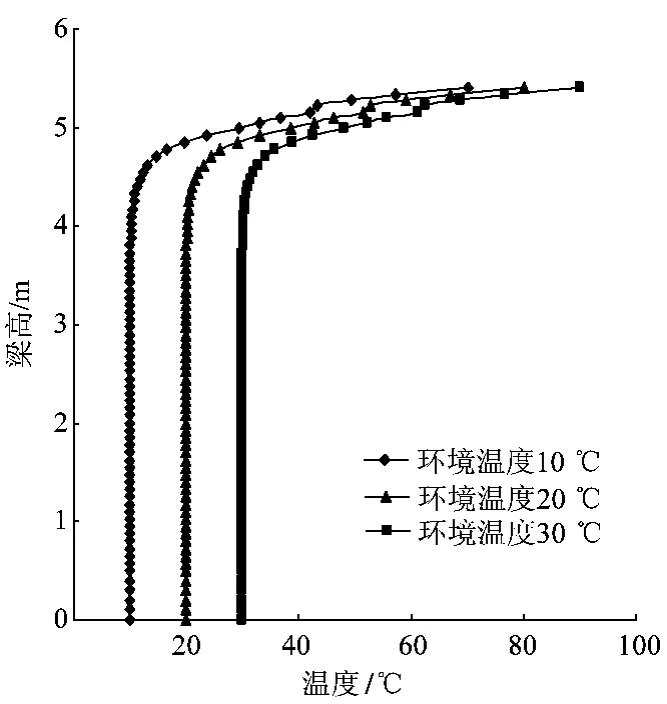
图5 梁高5.4 m温度沿高度分布

相同截面高度的轨道梁，在温差作用下，随着环境温度的增高，梁的整体温度增高，变化趋势相似。

不同跨度和截面高度，相同温度荷载下，随着截面高度的增高，底部温度不变的区域变大，上部温度变化相似。可以看出，距离顶部0～1.5 m是温度变化区域，距离顶部1.5 m到底部之间，温度变化为0。这是由于磁浮轨道梁上部是承接磁悬浮列车的，上部结构有一定的限制。无论跨度怎么改变，轨道梁截面顶部的宽度和承接磁浮列车的高度有具体的参数限制，所以截面沿温度变化会体现一致性。

综合上述分析，可以总结出磁悬浮轨道梁在温差荷载作用下的温度分布图及温差分布图。取所有模型的温差平均值，给出推荐的温度梯度计算图，见图6。

3.2 位移分析

从ANSYS结果文件中得到梁的位移曲线。在温度荷载作用下，简支梁跨中达到位移最大值。在不同气温环境下，相同的温度差值使得跨中的挠度有细微差别，差别并不大(见表1)。可以看出，在温差作用下，中低跨度磁浮梁的跨中挠度均 ＞1/6 500。现在运行的磁浮轨道交通并不能满足现有规定的温度位移要求。

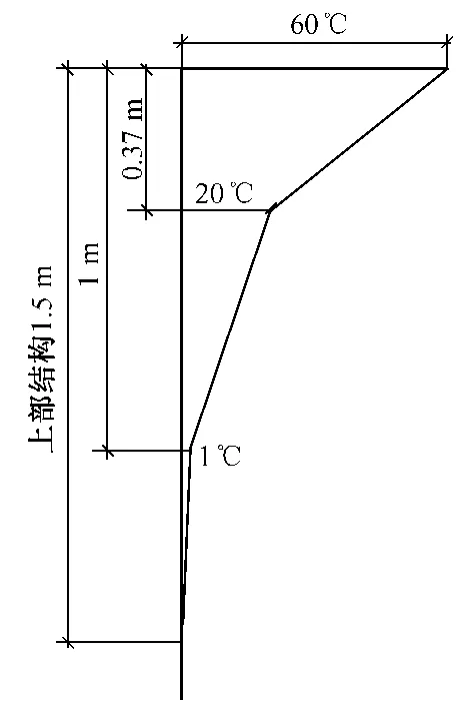
图6 轨道梁温度梯度

表1 截面高度对应位移及挠跨比

表1所取截面都不能满足现有规定。随着跨度的增大，温度的影响作用变小。即对于中低跨度的梁，温差位移可能是结构位移的影响因素。为了验证是否要求过严，计算了截面高度为2.2 m的上海磁浮轨道梁在满足现有规定的位移要求下所能承受的温差(表2)。可以看出，满足规定挠跨比1/6 500的梁所能承受的温度差值为15℃。然而在现实生活中，上下梁表面＞15℃温差情况下并没有造成破坏。这说明规定过于严格，应给予适当放松。

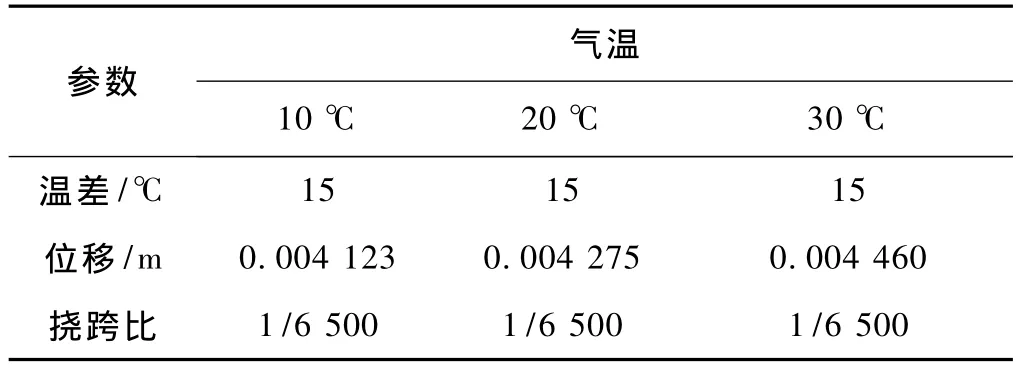
表2 满足现有规范的温差及位移

4 结论

1)根据现有规定，当轨道梁上下表面承受60℃温度差值时，梁的最大位移与梁长的比值需小于1/6 500。计算不同跨度不同截面的轨道梁在温差作用下的位移，梁跨中最大位移均大于1/6 500。不满足现有要求。

2)计算满足现有要求的轨道梁，结果显示梁只能承受15℃的温度差值，说明现有规定过于严格，应给予一定放松。

3)参考各国给出的规范，结合本文九个模型综合分析，给出了温度梯度模式。

［1］孔祥谦.有限单元法在传热学中的应用(第三版)［M］.北京:科学出版社，1998.

［2］DILGER W H，GHALI A，CHAN M，et al.Temperature stresses in composite box girder bridges［J］.JournalofStructural Engineering，ASCE，1983，109(6):1460-1478.

［3］BRANCO F A，MENDES P A，MIRAMBELL E.Heat of hydration effects in structures［J］.ACI Material Journal，1992，89(2):139-145.

［4］SAETTA A，SCOTTA R，VITALIANI R.Stress analysis of concrete structures subjected to variable thermal loads［J］.Journal of Structural Engineering，1995，121(3):446-457.

［5］王鹏，叶仁亦，翁艾平.基于ANSYS下混凝土箱梁水化热温度场的有限元计算［J］.铁道建筑，2008(2):10-13.

［6］王化光，黄育龙.鄂东长江公路大桥索塔日照变形监测及应用［J］.铁道建筑，2010(3):14-17.

［7］刘兴法.混凝土结构的温度应力分析［M］.北京:人民交通出版社，1991.