连续梁桥上典型道岔群纵向受力与变形分析
2011-05-04刘哲,王平
刘 哲,王 平
(西南交通大学 高速铁路线路工程教育部重点实验室,成都 610031)
由于我国幅员广阔,受环保、节约用地要求或地形条件的限制,客运专线建设中一些车站必须设置在大桥或特大桥上,从而出现多组无缝道岔相互连接形成桥上无缝道岔群的情况。由于连续梁桥整体性较好,可为无缝道岔提供一个整体连续、各向稳定的铺设平台,且客运专线多为双线铁路,因而连续梁桥上双线两组道岔对称布置和咽喉区外侧的单渡线是主要的道岔群布置形式[1]。为了指导和完善连续梁桥上铺设无缝道岔群时道岔和桥梁的设计方法,本文以这两种常见道岔群工况为例,分析无缝道岔群在连续梁桥上的纵向受力与变形规律。
1 计算模型及工况参数
1.1 计算模型
道岔—桥梁相互作用原理定义如下:在梁体温度变化、列车荷载、列车制动/加速以及道岔里轨随温度变化伸缩的作用下,梁和桥上道岔之间产生相对位移,桥上道岔产生钢轨纵向附加力,对桥面系作用大小相等、方向相反的反作用力,此力通过梁、支座传递至墩台,在桥上道岔与桥梁之间形成一个相互作用的力学平衡体系。可见,钢轨、岔枕、桥梁及墩台是一个相互作用、相互影响的耦合系统,只有建立道岔—桥梁—墩台一体化模型[1-7],才能弄清道岔及桥梁的受力与变形规律。计算模型如图1所示。
模型中将钢轨按扣件支承点划分为杆单元,岔枕按钢轨支承点划分为梁单元,梁体按枕孔划分为梁单元,墩台、扣件、道床、限位器、间隔铁均采用线性或非线性弹簧单元模拟。钢轨通过扣件单元与岔枕相连,岔枕通过道床单元与桥梁相连,辙跟通过限位器单元与基本轨相连,心轨跟端通过间隔铁单元与翼轨相连,桥梁固定支座处用墩台单元与基础相连,桥梁外的钢轨与基础相连,仅考虑结构的纵向相互作用。模型中道岔可为单组或道岔群,桥梁可为简支梁、连续梁或其它梁型。
1.2 计算参数
计算中道岔为60 kg/m钢轨客运专线18号可动心轨道岔,有砟轨道线路纵向阻力按12 kN/枕计算,岔区每枕纵向阻力按枕长分布为4.6 kN/m,轨枕间距为0.6 m。Ⅱ型扣件常阻力值取12.5 kN/组。道岔采用双限位器,其阻力取为分段线性阻力,当限位器子母块贴靠,两轨相对位移小于1 mm时,限位器阻力取为150 MN/m;当两轨相对位移大于1 mm时,限位器阻力取为60 MN/m,限位器子母块间隙取为7 mm。道岔长翼轨间隔铁阻力采用线性阻力,取为50 MN/m。两边桥台的墩台纵向刚度为100 MN/cm,简支梁桥墩的刚度均为1 MN/cm,连续梁桥墩的刚度为10 MN/cm。各梁跨均为箱梁,截面形心距上翼缘为1.626 6 m,距下翼缘为1.577 4 m,截面惯性矩为3.704 4 m4/线。
计算中道岔温度变化为50℃,桥梁温度变化为15℃。
1.3 计算工况

图1 道岔—桥梁—墩台一体化计算模型
1)工况一:单组道岔
计算中以单组桥上无缝道岔作为对比工况,道岔与桥梁布置如图2所示,梁跨为(32+48+32)m连续梁,两边各布置3跨32 m简支梁,各梁跨均为双线整体箱梁,无缝道岔位于连续梁正中,连续梁固定支座位于道岔前端。

图2 单组道岔
2)工况二:双线两组道岔对称布置
道岔与桥梁布置如图3所示,梁跨和支座布置与工况一相同,简支梁为双线整体箱梁,岔前、岔后两正线位于同一片箱梁上,岔后两站线位于道岔梁或简支T梁上,与正线上的简支梁箱梁不为整体桥面;连续梁为四线整体箱梁;桥墩与桥面结构相似,简支梁桥墩两正线下为一整体,站线桥墩与正线桥墩分离,连续梁桥墩四条正线下均为一整体,两组道岔均位于连续梁正中。

图3 双线两组道岔对称布置
3)工况三:单渡线道岔
道岔与桥梁布置如图4所示,梁跨为3×32 m+6×32 m+3×32 m,各梁跨均为双线整体箱梁,连续梁固定支座位于正中,单渡线道岔反对称布置于连续梁正中。

图4 单渡线道岔
2 计算结果与分析
2.1 双线两组道岔对称布置
直基本轨伸缩附加力分布及与单组道岔的比较如图5所示,图中X为距左桥台的距离,向右为正;P为道岔直基本轨的伸缩附加力,以压力为正。从图中可见,两组道岔对称布置与单组道岔基本轨温度附加力分布相同,最大伸缩附加力出现在连续梁左端梁缝处,比单组道岔略大。其他计算结果与单组道岔的比较如表1所示,表中钢轨位移及墩台纵向力以向右为正。从表1中可见,两组道岔对称布置与单组道岔钢轨伸缩位移及传力部件受力相当,而各墩台受力增大一倍。

图5 双线对称布置的两组道岔温度附加力
2.2 单渡线道岔
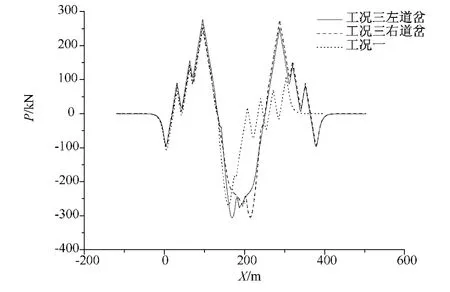
图6 单渡线道岔温度附加力
左右侧道岔直基本轨温度附加力分布及与单组道岔的比较如图6所示。图中X为距左桥台的距离,向右为正;P为道岔直基本轨的伸缩附加力,以压力为正。从图中可见,左右侧道岔基本轨温度附加力呈反对称分布,在岔前连续梁端部最大值约为277.7 kN,在岔后连续梁端部最大值约为252.2 kN。虽然单渡线道岔连续梁最大温度跨度为128 m,但由于采用对称布置,左右道岔作用于桥梁上的纵向力相互抵消,连续梁端部最大温度附加力仅比单组道岔72 m温度跨度情况下的最大温度附加力261.9 kN略大。

表1 计算结果
3 结论
1)两组道岔对称布置时与单组道岔基本轨温度附加力分布相同,钢轨伸缩位移及传力部件受力也相当,各墩台受力增大一倍,说明在两道岔对称布置时,可按单组道岔进行计算,墩台承受两组单开道岔的传力。
2)由于单渡线道岔采用对称布置,左右道岔各项计算结果是对称的,基本轨温度力及基本轨伸缩位移较单组道岔略大,但传力部件受力、尖轨及心轨伸缩位移要小于单组道岔,说明单渡线这种岔桥布置对道岔受力是较为有利的。
3)单渡线道岔前后简支梁墩台受力不到单组道岔的2倍,连续梁固定墩几乎不受力,说明单渡线这种岔桥布置对桥梁受力是十分有利的。
[1]王平,刘学毅.无缝道岔计算理论与设计方法[M].成都:西南交通大学出版社,2007:254-257.
[2]王平.无缝道岔群对钢轨位移和纵向力的影响研究[J].铁道学报,2002,24(2):74-78.
[3]刘衍峰,高亮,冯雅薇.桥上无缝道岔受力与变形的有限元分析[J].北京交通大学学报,2006,30(1):66-70.
[4]杨荣山,刘学毅,王平.简支梁桥上无缝道岔纵向力影响因素分析[J].西南交通大学学报,2008,43(5):666-672.
[5]杨荣山,刘学毅,王平.桥上无缝道岔纵向力计算理论与试验研究[J].铁道学报,2010,32(4):134-140.
[6]曾志平,陈秀芳,赵国藩.连续梁桥上无缝道岔伸缩力与位移计算[J].交通运输工程学报,2006,6(1):34-38.
[7]蒋金洲.桥上无缝线路钢轨附加纵向力及其对桥梁墩台的传递[J].中国铁道科学,1998,44(2):67-75.
[8]杨冠岭,陈小平,王平.桥上纵连板式无缝道岔计算软件开发与应用[J].铁道建筑,2010(12):87-90.
