洞室轴线走向与初始地应力关系对围岩稳定性的影响
2011-05-04李曼,马平,孙强
李 曼,马 平,孙 强
(1.中国国土资源航空物探遥感中心,北京 100083;2.中国科学院 地质与地球物理研究所工程地质力学重点实验室,北京 100029;3.北京交科公路勘察设计研究院有限公司,北京 100091;4.中国矿业大学 资源与地球科学学院,江苏 徐州 221116)
隧道轴线及大型地下洞室长轴轴线方位布置是地下结构设计的重要课题。地下洞室的轴线方向主要由整个枢纽布置和地质条件(岩体岩性、岩层走向、初始地应力和主要构造断裂面、主要软弱带等)决定。在岩体完整、地应力较高的岩体中开挖洞室时,洞室的轴向布置和初始地应力的关系对洞室围岩的稳定有较大影响。目前,系统研究地应力与洞室围岩稳定关系的文献较少,大多是通过二维或三维弹塑性有限元数值模拟研究具体工程开挖支护应力和位移,探讨地应力与洞室稳定的关系。另有些研究者通过弹性力学解析结果认为,洞室长轴轴线应与最大水平地应力方向一致,或尽量减小其夹角[1]。据此相关规范及设计手册有明确的原则性指示和规定:“隧洞的轴线方向宜与最大水平地应力方向有较小夹角”[2]。在岩体完整、地应力较高的深埋岩体中开挖地下洞室时,洞室轴线布置和初始地应力的关系对洞室围岩的稳定性起着决定作用。当研究区初始地应力场的性质不同时,洞室轴向取向不同,洞室围岩内的重分布应力不尽相同,有关这方面的研究今后仍需深入探讨。本文采用弹性力学方法,从理论上来讨论初始水平地应力与铅直地应力的比值不同时,地下洞室围岩重分布应力对洞室轴向选取的响应,进而从岩体地应力角度来评价隧道洞室围岩的稳定性。
1 圆形地下洞室围岩重分布应力对轴线取向的响应
当地下洞室断面形状为圆形时,假设洞室半径为R0,作用于洞室顶板及边墙围岩内的天然应力分别为σv和σh(图1),则洞室开挖后作用于洞壁上的重分布应力为[3]

则圆形洞室洞壁处的应力可表示为
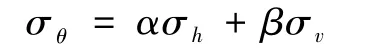
式中,α =1-2cos2θ;β=1+2cos2θ。
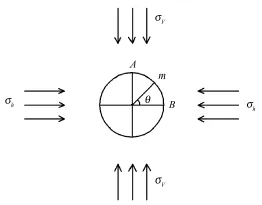
图1 地下隧道断面形状为圆形时的应力
在工程区开挖圆形地下洞室,开挖后洞室洞壁上的应力重新分布,重分布应力与初始地应力密切相关,初始地应力场的性质决定着洞室洞壁重分布应力的性质。对一般工程而言,地应力是随空间而变化的非稳定场[4-5]。当工程区 λ取值不同,而其它地质条件完全相同时,开挖相同尺寸的圆形隧道,作用于洞室洞壁上的重分布应力完全不同。令λ=σh/σv,当地下洞室轴线方向选取不同时,λ的取值介于σhmin/σv和σhmax/σv之间。
当最大水平主应力 σhmax与最小水平主应力 σhmin的差值不大时,即λ=1,不论地下洞室轴线走向为哪个方位,在洞室岩体内分布的重分布应力为压应力,且变化都不大。此时工程区的初始地应力场对地下洞室轴线的取向影响不大,洞室轴线的方向可根据整个工程的布局,综合考虑进行确定。
当最大水平主应力 σhmax与最小水平主应力 σhmin的差值较大时,地下洞室轴线的取向不同,λ取值不同,在洞室岩体内分布的重分布应力相差很大,此时洞室轴线的取向对洞室围岩的稳定性有比较大的影响。现分两种情况进行讨论:当λ≤1/3或λ≥3时,洞室洞壁上出现拉应力集中;当1/3<λ<3,且λ≠1时,洞壁围岩内的重分布应力σθ全为压应力。
假设:无论洞室轴线取向如何,洞室顶、底部的重分布应力为 σ'θ,两侧壁上的重分布应力为 σ″θ。当洞室轴线方向与最大水平主应力σhmax的方向一致时,作用于洞室顶、底部处的重分布应力为σ'θ1,作用于洞室两侧壁上的重分布应力为 σ″θ1;当洞室轴线方向与最小水平主应力 σhmin的方向一致时,作用于洞室顶部、底部处的重分布应力为 σ'θ2,作用于洞室两侧壁上的重分布应力为 σ″θ2。
1)当λ≤1/3或λ≥3时,洞室洞壁上出现拉应力集中现象,但洞室轴线方向取向不同,洞壁上重分布应力的大小并不完全相同。
当 λ≤1/3 时,洞室顶、底部(90°,270°)的重分布应力 σ'θ(α>0,β <0),σ'θ≤0,重分布应力为零或出现拉应力集中现象;在洞室两侧壁上(0°,180°)的重分布应力 σ″θ(α <0,β>0),σ″θ>0,出现压应力集中现象,于 是 可 得 0 ≥ σ'θ2>σ'θ1,σ″θ1>σ″θ2>0,则
当 λ≥3 时,洞室顶、底部处(90°,270°)的重分布应力 σ'θ(α>0,β <0),σ'θ>0,出现较高的压应力集中现象;在洞室两侧壁上(0°,180°)的重分布应力 σ″θ(α <0,β>0),σ″θ≤0,重分布应力为零或出现拉应力集中现象,于是可得 σ'θ2>σ'θ1>0,0≥σ″θ1>σ″θ2,则
总之,当λ≤1/3或 λ≥3时,在洞室洞壁上都会有拉应力集中现象发生,而岩石自身的抗拉性能很差。为此,在实际工程中,如果在洞室洞壁内不能避免产生拉应力集中的现象,也应使洞壁岩体内产生的拉应力最小,以便最大程度地降低工程造价。因此,当λ≤1/3时,地下洞室轴向方向宜与最小水平主应力 σhmin的方向一致或呈小角度相交;当λ≥3时,地下洞室轴线方向宜与最大水平主应力σhmax的方向一致或呈小角度相交。
2)当1/3<λ<3,但 λ≠1时,洞室洞壁围岩内的重分布应力 σθ,全为压应力。在洞室顶、底部(90°,270°)的重分布应力 σ'θ(α>0,β <0),σ'θ>0,出现压应力集中;在洞室两侧壁上(0°,180°)的重分布应力σ″θ(α <0,β>0),σ″θ>0,出现压应力集中。但此时洞室轴线方向不同时,洞室洞壁上的压应力集中程度也并不相同。
当 1/3<λ <1时,σ″θ-σ'θ=4(σv-σh)>0,若洞室轴线方向与最小水平主应力 σhmin的方向一致时,σ″θ- σ'θ的值较小。
当1<λ <3时,σ'θ-σ″θ=4(σh-σv)>0,若洞室轴线方向与最大水平主应力 σhmax的方向一致时,σ'θ- σ″θ的值较小。
当地下洞室洞壁上的重分布应力全为压应力时,应使压应力间的差值最小,亦即使洞壁上的压应力分布比较均匀,洞室的稳定性才最好。因此,当1/3<λ且λ<1时,地下洞室轴线方向宜与最小水平主应力σhmin的方向一致或呈小角度相交;当1<λ<3时,地下洞室轴线方向宜与最大水平主应力σhmax的方向一致或呈小角度相交。
2 其它形状地下洞室围岩重分布应力对洞室轴线取向的响应
对于其他形状的地下洞室(矩形、圆拱直墙型等地下洞室),其洞室围岩的重分布应力 σθ也可用式σθ=ασh+βσv表示,但不同形状的地下洞室,α、β的表达式并不相同。因此,在地下开挖不同形状的洞室时,洞室顶、底及侧墙有拉应力出现时,λ的取值范围完全不同,且与洞室的形状密切相关。
令 p、q(其中0 <p<1,q>1,洞室形状不同,p、q取值不同)分别为洞室顶、底板及两侧壁出现拉应力时的λ值,经推导可得出:
若λ≤p或λ≥q,洞室洞壁上会出现拉应力集中,为最大程度地降低洞室洞壁上拉应力集中的程度,且拉、压应力分布比较均匀,λ≤p时,洞室轴线取向宜与最小水平主应力σhmin的方向一致,λ≥q时,洞室轴线取向宜与最大水平主应力σhmax的方向一致。
若p<λ<q且λ≠1,洞室洞壁上的重分布应力全为压应力,此时为使洞周应力分布较为均匀,p<λ<1时,洞室轴线取向宜与最小水平主应力 σhmin的方向一致,1<λ<q时,洞室轴线取向宜与最大水平主应力σhmax的方向一致。
若λ=1,洞室洞壁上重分布应力仍为压应力,但在此种初始应力场中开挖地下洞室时,无论洞室轴线走向为哪个方位,洞室洞壁上的重分布应力都是一样的。此时工程区的初始地应力场对地下洞室轴线的取向影响不大,洞室轴线的方向可根据整个工程的布局,综合考虑进行确定,这与圆形洞室的结论是一致的。
3 结论
在深埋完整岩体内开挖地下洞室时,洞室轴线的走向与工程区初始应力场的性质密切相关。为尽最大可能地发挥洞室围岩的自稳能力,降低工程造价,应尽量使洞室洞壁上的应力分布比较均匀,且应避免洞壁上有拉应力集中的现象出现。如果无法避免时,也应使拉应力为最小。因此,如果工程区的初始地应力以水平应力为主,即λ=σh/σv>1,则开挖洞室轴线方向宜与最大水平主应力σhmax的方向一致或呈小角度相交;如果工程区的初始地应力以自重应力为主,即λ=σh/σv<1,则开挖洞室轴线方向宜与最小水平主应力σhmin的方向一致或呈小角度相交。
[1]王俊奇,颜月霞.地应力对洞室轴线布置影响的二维数值分析[J].长江科学院院报,2009,26(7):33-39.
[2]中华人民共和国水利部.SL279—2002 水工隧洞设计规范[S].北京:中国标准出版社,2002.
[3]刘佑荣,唐辉明.岩体力学[M].武汉:中国地质大学出版社,1999:42-167.
[4]谷兆祺,彭守拙,李忠奎.地下洞室工程[M].北京:清华大学出版社,1994:35-79.
[5]GAL E W J,BLADKWOOD R L.Stress Distribution and Rock Failure Around Coal Mine Roadways[J].Int J Rock Failure Mech Min Sci& Geomech Abstr,1987,24(3):165-173.
