基于局部连续场的重力匹配辅助导航
2011-04-30童余德边少锋蒋东方向才炳
童余德,边少锋,蒋东方,向才炳
(海军工程大学 导航工程系,武汉 430033)
惯性导航系统的定位误差随时间积累发散,无法长时间保持高精度,考虑到潜艇长期潜航及隐蔽性要求,有必要借助另外一种无源的辅助导航手段实时或定期校正 INS。重力匹配辅助惯性导航技术由于具有完全自主性和高隐蔽性,且重力场较稳定,该技术已引起各国极大的关注。其代表性产品包括美国Lockheed Martin公司研制的由通用重力模块(UGM)所组成的重力导航系统(NGS)和贝尔实验室研制的重力辅助导航系统(GAINS)。
匹配算法是重力辅助惯性导航技术中的核心问题。匹配算法包括基于卡尔曼滤波的匹配算法和相关极值匹配算法两类。基于卡尔曼滤波的匹配算法主要有SITAN(Sandia Inertial Terrain-Aided Navigation)算法。该算法采用多模型自适应估计(Multiple Model

图2 随机初值迭代相关极值匹配算法流程图Fig.2 Flow chart of maximum correlation for matching with random initial values
3 仿真实验分析
局部连续解析重力异常场相关极值匹配算法仿真实验基于 MATLAB平台实现的。为方便仿真验证,直接采用peaks函数组合成局部连续重力异常场作为仿真用真实背景场,该连续重力异常场解析表达式如式(4)所示,其3D示意图如图3所示。

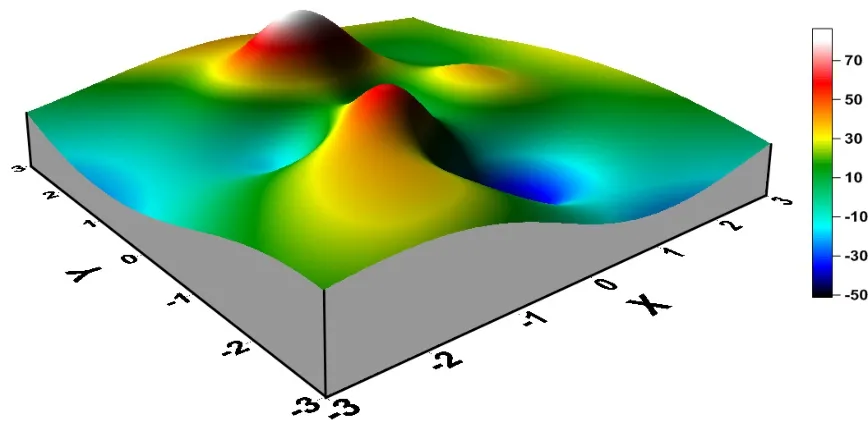
图3 局部连续重力异常场三维图Fig.3 3D map of local continuous gravity anomaly field
设定序列点数为 21,采样点距为 0.141,迭代次数为 5。为验证算法最佳精度,首先设计一组在理想条件下的仿真实验(即重力观测噪声,惯导指示航迹误差均为零)。调用本文设计的相关极值匹配算法分别在理想仿真条件下进行仿真试验得到仿真结果如图4所示(匹配过程图经局部放大处理)。
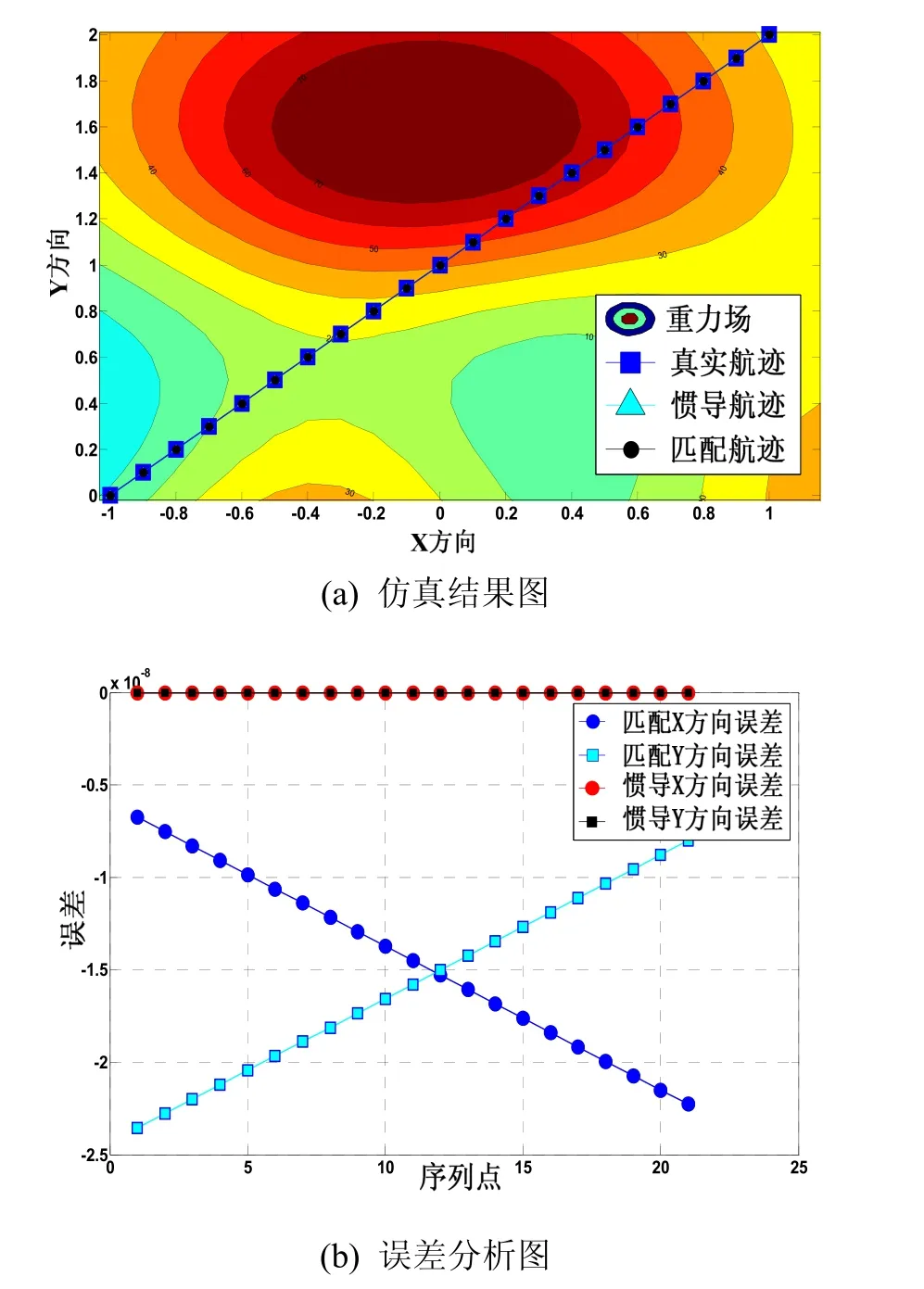
图4 理想条件下匹配仿真实验Fig.4 Matching simulation tests under ideal conditions
从匹配结果图中可以看出连续场相关极值匹配算法在理想条件下能达到 1 0-8级的精度(由于计算机本身存在数值计算误差,此时惯导误差达到 1 0-17级精度),与理论分析相符。考虑到局部连续重力场与真实重力场之间的误差及重力仪观测误差,将重力量测噪声取均方差为10 mGal2的高斯白噪声。指示航迹误差分别设(0.2,0.3,0),(0,0,π/18),(0.2,0.3,π/18)(注:括号内第一个值为序列质心点X方向误差,第二个值为序列质心点Y方向误差,第三个值为航向误差)。调用本文设计的相关极值匹配算法分别在上述的三种仿真条件下进行仿真试验得到仿真结果如图 5~7所示(仿真结果图经局部放大处理)。
从三组不同误差条件下仿真实验结果图可以看出,在重力观测误差较大的情况下,不论是对纯漂移误差还是纯航向误差或者是两者的组合,该相关极值匹配算法均能以较高精度对真实航迹进行估计。从三组实验结果图中的重力异常值比较图可以清晰地看出,匹配位置上的重力异常值与真实航迹上重力异常真值吻合良好,进一步说明了算法的有效性。三组实验中重力异常测量值、惯导指示位置重力异常、匹配位置重力异常值与真实位置重力异常值之间的 MSD指标比较如表1所示。从表中可以看出,匹配位置重力异常值与真值之间 MSD值远远小于惯导指示位置重力异常与真值之间 MSD值,且从本文的三个仿真实验来看均小于重力量测值与真值之间 MSD值,更客观的说明了连续场相关极值匹配算法准确性。
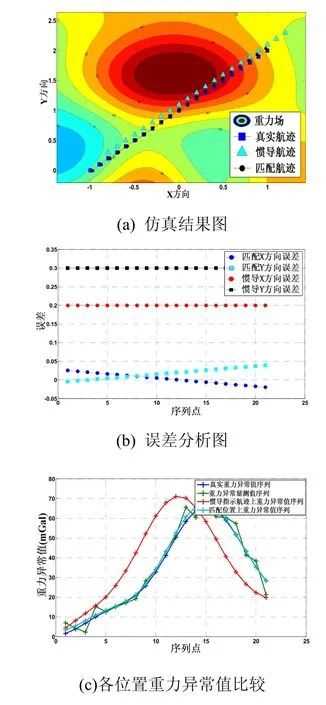
图5 匹配仿真实验一Fig.5 The first matching simulationexperiment

图6 匹配仿真实验二Fig.6 The second matching simulationexperiment

图7 匹配仿真实验三Fig.7 The third matching simulation experiment

表1 各位置重力异常值与真值间MSD指标对比Tab.1 Contrast of the MSD between real gravity anomaly and the gravity anomaly on each sort position
4 结束语
重力匹配辅助导航是组合导航技术发展的一个崭新的方向。相关极值匹配算法原理简单且精度较高,可操作性强。本文提出的基于局部连续重力异常场相关极值匹配算法采用随机初值迭代的方式能够实现全局寻优(由于篇幅所限,对于如何由离散场获取具有统一解析式的连续场的问题,本文未作论述)。最后的仿真实验说明,不论是对纯漂移误差还是纯航向误差或者是两者的组合,该相关极值匹配算法均能收敛到全局最优解。
(References):
[1] Behzad K P, Behrooz K P. Vehicle localization on gravity maps[C]// Proceedings of SPIE- The International Society for Optical Engineering, 1999, 3693: 182-191.
[2] Bishop C. Gravitational field maps and navigational errors[J]. IEEE Journal of Oceanic Engineering, 2002,27(3): 726-737.
[3] 吴太旗,黄谟涛,边少锋,等. 直线段的重力场匹配水下导航新方法[J]. 中国惯性技术学报,2007,15(2):202-205.WU Tai-qi, HUANG Mo-tao, BIAN Shao-feng, et al.New gravity matching algorithm for underwater navigation based on straight-line[J]. Journal of Chinese Inertial Technology, 2007, 15(2): 202-205.
[4] Wang Zhigang, Bian Shaofeng. A local geopotential model for implementation of underwater passive navigation[J]. Progress in Natural Science, 2008, 18(9):1139-1145.
[5] Wu L, Gong J Q, Cheng H, et al. New method of underwater passive navigation based on gravity gradient[C]// Proc. of SPIE, 2007: 6790 67901V1-67901V8.
[6] Jamshaid Ali, Fang J C. SINS/ANS integration for augmented performance navigation solution using unscented kalman filtering[J]. Aerospace Science and Technology, 2006, 10(3): 233-238.
[7] Xiao Sheng-hong, Bian Shao-feng. Research on regional model of continuous fourier series of marine magnetic anomaly field using for the geomagnetic navigation[C]//International Conference on Industrial and Information System, 2010: 437-440.
[8] Cowie M, Wilkinson N, Powlesland R. Latest development of the TERPROM(digital terrain system[C]∥ Position,Location and Navigation Symposium, 2008: 1219-1229.
[9] Yabe H, Ogasawara H, Yoshino M. Local and superlinear convergence of quasi-Newton methods based on modified secant conditions[J]. Journal of Computational and Applied Mathematics, 2007, 205: 617-632.
[10] 刘飞,周贤高,杨晔,李士心. 相关地磁匹配定位技术[J]. 中国惯性技术学报,2007,15(1):59-62.LIU Fei, ZHOU Xian-gao, YANG Ye, LI Shi-xin.Geomagnetic matching location using correlative method[J]. Journal of Chinese Inertial Technology, 2007, 15(1): 59-62.
