激活学生积极思维的有效策略

何红亚

培养学生的思维能力是数学课堂教学中研究和探索的重要问题。在数学教学中，我们要为学生提供充分的进行思维活动的时间和空间，让学生经历学习探究的过程，激活学生主体需要的心理状态，适应不同层次学生的发展需要，以教师的教学智慧生长为学生的学习智慧，实现教与学真正的思维互动。

一、利用“失败”，点燃思维

失败是资源，它包含着经验和教训，为正确思维提供了比照对象。在实际教学中，教师往往只看到成功，忽视了失败的价值。其实，“失败”这一教学资源，对学生认知结构的完善、改造和重建能起到推波助澜的作用，有效利用“失败”，最终实现认知结构的构建，呈现有意义的学习。

苏教版第十册《圆的认识》中画图的教学，大多数教师是让学生用各种方法尝试画圆，画好后请成功的学生交流画圆的方法，最后教师总结画圆的方法。然而，在教学中抓住学生的失败，深度剖析，让学生深刻掌握画圆的方法，学生将受益匪浅。

师：怎样画一个圆？你有好办法吗？

生1：用杯子底部的圆能照样子画出一个圆。（教师拿出杯子，学生上台示范画圆）

生2：用硬币，绕硬币一圈画出的也是一个圆。（学生在实物投影仪上示范画圆）

师：用物体上的圆来画圆，这是一个方法，还有其他方法吗？

生：老师，我可以用圆规画圆。

师：对！圆规是画圆的工具，可以画出大小不同的圆。请同学们用圆规在纸上画一个圆，试试看！

师：我想先请没有画成功的同学谈谈你用圆规画圆的困惑。（老师发现有的同学画成功了，有的同学没有画成功）

生1：（学生把自己画的圆放在展示台上）我画圆时旋转过程中不小心动了这个脚（指带针尖的脚），所以圆的边跑外面去了，变形了！

师：那你有什么建议和大家分享？

生1：画圆时针尖一端要固定不动。

生2：老师，我要补充，我也没画成功，我画的时候，笔芯的脚向外移动了，我觉得画的时候针尖滑动是我用力太猛，所以，要固定针尖一端后，重心在针尖处，再用力均匀地旋转另一个脚，保证两只脚不移动，就能画成一个圆。

师：说得好，能从失败中总结经验教训，这是学习的好方法！就请你来画一个圆，相信你会成功的。（生2在众目睽睽下镇定自若，画出了一个圆）

师：画成功的同学也来说说怎样才能画好一个圆，请你边画边说。

生：要先固定针尖的一个点（定点），再张开圆规两脚（定长），最后旋转一周，就画成了这个圆。

师：看来，画圆有三部曲：定点、定长、旋转一周。同学们，画好一个圆，你们有信心了吗？（有）请再画一个圆给大家欣赏吧！

这一教学过程，不难看出，学生不仅掌握了画圆的基本方法，同时学生在经历失败的过程中，自我总结、反思，真切感受画圆的技巧，更重要的是利用“失败”激发了学生敢于和善于剖析问题的勇气和热情，点燃了思维的火花，学生的思维得到真正意义上的明晰，实现了认知结构的重建。

二、呈现过程，激荡思维

自主探索是思维铺展的过程，也是深入学习的过程。现实教学中，老师往往注重结果，忽视学习过程的充分展开，人为精简学生的思维，弱化了思维能力的培养。教学中，引导学生展示思考的历程，一方面教师可以感知学生的所思所想，调整教学策略；另一方面，可以为学生提供更丰富的思维交流的内容，通过学生相互分析和反思、肯定和否定实现思维的深化和认知的重建。

案例一 《倍数和因数》的教学片段（聚焦结果）

师：36的因数有哪些？请同学们自己去探索，把所有的因数都写出来。（学生独立思考并探索）

师：（反馈）你是怎么找的？和大家交流一下。

生：我想除法算式36÷（ ）=（ ）。

师：哦，你是想36÷（ ）=（ ），除数是从几开始找的？

生：从1开始。

师：很好，往下呢？

生：是2、3、4……

师：（根据问答有序呈现算式）

36÷1=3636÷2=1836÷3=12

36÷4=9 36÷5（不行）

36÷6=6 36÷7（不行）

36÷8（不行）36÷9=4（重复了）

师：我们找到重复为止就不要找下去了。

案例二 《倍数和因数》的教学片段（聚焦过程，关注结果）

师：36的因数有哪些？请想一想，你准备怎样找？

生1：（学生独立思考片刻后）我准备从除法算式36÷（ ）=（ ）来找。

生2：我准备根据乘法算式（ ）×（ ）=36来找。

师：很好，按照你喜欢的方法找出36的因数吧，注意一边写下算式，一边写出找到的因数，注意要找完整哦！

（学生开始忙碌起来，教师巡视，观察学生中出现的种种情况，捕捉教学信息）

师：下面让我们一起来交流和分享你们的探究成果。根据除法算式的谁愿意来展示你的思考过程？

生1：36÷2=1836÷6=6

36÷4=9 36÷3=12

36的因数有：2、18、6、4、9、3、12

生2：36÷1=3636÷2=18

36÷3=1236÷4=9

36÷5（不行）36÷6=6

36÷7（不行）36÷8（不行）

36÷9=4（重复了）

36的因数有：1、36、2、18、3、12、4、9、6

师：同样根据除法算式找36的因数，你欣赏哪一种？为什么？

生1：我欣赏第二种，因为第二种找全了，第一种漏了36÷1=36。

生2：我也欣赏第二种，因为它从除数为1开始找，是有次序依次往下找的，不容易漏掉。

生3：第二种还把不行的也列举出来了，这样更清楚，不容易搞错。

生4：第二种找到第一个重复的数就不往下找了，因为后面的都重复了。

师：同学们讲得很有道理，在想除法算式找因数时，我们从除数是几开始考虑？

生：从1开始，依次是1、2、3、4、5……这样找就不会遗漏也不会重复。

生2：有序找的时候出现第一个重复的数就可以不往下找了。

师：是这样吗？让我们继续往下写一写，看看是不是如大家所说。（师生一起往下有序列举）的确如同学们所发现的，出现第一个重复的数以后后面的因数都重复了，所以我们只要找到第一个重复的数出现为止。

生：老师，用乘法算式（ ）×（ ）=36找，也应该从1开始有次序地找36的因数。

……

上述两个案例告诉我们，只注重结果，会造成教学中的急功近利，过早地和盘托出，表面上看教学任务完成得很“顺利”，但实际是造成顺畅背后思维空间的收缩，充分暴露学生学习思考的过程，通过学生之间思维的碰撞，相互间的评价，以学生的思维发展为教学生长点，这样的教学活动才能更好地促进知识的内化和思维的生长。

三、组织交流，激活思维

语言是思维的外壳，反映人思维的精准程度。善于交流表达的人，概念清晰，思维流畅。同时，我们也不难发现学生灵动的语言能缔造活泼生动的课堂。因而，教学中要努力引发学生的交流欲望，以交流触发学生思维的敏感度，激活学生的主体思维状态。

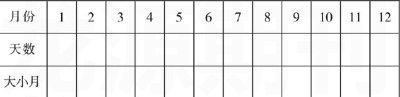
如教学《年、月、日》一课时，课前我布置学生收集身边的年历，帮助学生积累年、月、日的相关信息，为课上人人交流奠定基础。教学中，首先让学生在小组内交流年、月、日的有关知识，这时每个学生都有话可说，发言积极，一些平时不爱发言的学生，因为有话可说而脸上洋溢着得意和快乐！接着，我组织全班交流，选择一些思维相对滞后的学生交流收集到的信息。这些学生的表现让我喜出望外，他们争先恐后地表达自己的想法：“我知道一年有12个月”“一个月有的31天，有的30天，有的28天，有的29天”“我还知道12个月中有大月小月之分，31天是大月，30天是小月”“我补充，二月很特殊，有时候28天，有时候29天”“一年中有平年和闰年之分”等等。学生的交流发言尽管不是很系统，有些也只是知其然、不知其所以然，但我们可以了解学生最真实的思维状态，从而调控教学进程。紧接着，设问：你们的发现都正确吗？还有什么没发现呢？同时要求学生利用年历表，进一步探索和验证自己获得的信息，并填写汇总表：

一年有（）月

为再次系统、准确交流提供依据，使交流质量螺旋式上升，最后在交流中师生共同归纳整理年、月、日的知识要点。

学生作为一个独立的生命体存在，其学习有一定的主观能动性，同时，不同个体之间的交流又存在着差异性，思维速度有快有慢，思维深度有深有浅，语言表达有流畅有生疏，因而组织学生交流，要尊重学生的差异性，切忌因追求教学过程的顺畅，而只重视思维超前学生的交流，忽视部分思维滞后学生的发言。我们要特别关注思维相对滞后的学生参与交流活动，浅显的问题尽量让其先说，较难的问题，提示他们说，维护这些学生主动思考的热情；难的问题让优等生说，使不同层次的学生都能分享学习的快乐。组织学生交流还要培养学生想说、敢说、会说的品质，在灵动的交流中凸现思维的张力。