大坝监测传感器线性度的计算方法探讨

陈欣刚 李玉梅

(1.水利部水文仪器及岩土工程仪器质量监督检验测试中心,南京 210012;2.南京水利水文自动化研究所,南京 210012)

传感器是一种检测装置,能感受到被测量的信息,并能将检测感受到的信息,按一定规律变换成为电信号或其他所需形式的信息输出,以满足信息的传输、处理、存储、显示、记录和控制等要求[1]。传感器通常由敏感元件和转换元件组成。是实现自动检测和自动控制的首要环节。传感技术就是应用于检测控制系统的信息采集技术,它与计算机技术、通信技术一起被称为信息技术的三大支柱。从仿生学观点来看,如果把计算机看成是处理和识别信息的 “大脑”,把通信系统看成是传递信息的 “神经系统”的话,那么传感器就是 “感觉器官”。

传感技术是关于从自然信源获取信息,并对之进行处理和识别的一门多学科交叉的现代科学与工程技术,它涉及传感器、信息处理和识别的规划设计、开发、制造、测试、应用及评价改进等活动。获取信息依靠各类传感器,它们有各种物理量、化学量或生物量。按照信息论的凸性定理,传感器的功能与品质决定了传感系统获取自然信息的信息数量和信息质量,是高品质传感技术系统的构造第一个关键。信息处理包括信号的预处理、后置处理、特征提取与选择等。识别的主要任务是对经过处理信息进行辨识与分类。它利用被识别 (或诊断)对象与特征信息间的关联关系模型对输入的特征信息集进行辨识、比较、分类和判断。因此,传感技术是遵循信息论和系统论的。它包含了众多的高新技术、被众多的产业广泛采用。它也是现代科学技术发展的基础条件,应当得到足够的重视。传感技术产业是最具有发展前途的高技术产业,它以其技术含量高、经济效益好、渗透能力强、市场前景广等特点成为全世界高新技术争夺的一个重要领域。

1 线性度和拟合直线

传感器有静态特性和动态特性[2],动态特性是反映传感器输出对于随时间变化的输入量的响应特性,而静态特性是指被测量的值处于稳定状态时的输出输入关系,输入量与输出量之间的关系式中不含有时间变量,即传感器的静态特性可用一个不含时间变量的代数方程,把与其对应的输出量作为纵坐标而画出的特性曲线来描述。大坝安全监测的对象随时间的变化速度通常较缓慢,因此多属于静态特性,故在本文中主要探讨传感器的静态特性。表征传感器静态特性的主要参数有线性度、灵敏度、迟滞、重复性、漂移等。本文着重分析直线拟合的几种方法对传感器线性度的影响。

传感器的输出与输入关系可分为线性特征和非线性特征。从传感器的性能看,希望具有线性关系,即具有理想的输出输入关系。但实际遇到的传感器大多为非线性,如果不考虑蠕变等因素,传感器输出与输入关系的拟合直线可用一个多项式表示:

x为输入量,y为输出量,a0为零位输出,表示没有输入 (x=0)时的输出值,a1为线性项常数,零时的输出量,a2,a3,…,an为非线性项系数。

静态特性曲线可通过实际测试获得。在实际使用中,为了标定和数据处理的方便,希望得到线性关系,因此引入各种非线性补偿环节。如采用非线性补偿电路或计算机软件进行线性化处理,从而使传感器的输出与输入关系为线性或接近线性。但如果传感器非线性的次方不高,输入量变化范围较小时,可用一条直线近似的代表实际曲线的一段,使传感器输入与输出特性线性化,所采用的直线称为拟合直线。

传感器的线性度是指传感器输出量与输入量之间的实际关系曲线偏离拟合直线的程度。定义为在全量程范围内实际特性曲线与拟合直线之间的最大偏差值与满量程输出值之比。

γL为线性度,Δ Lmax为实际特性与拟合直线的最大偏差,YFS为满量程输出值。

线性度是描述传感器静态特性的一个重要指标,又叫非线性误差,也是组建测试系统选择传感器的一个依据。在传感器的技术实践中,结合实验样本,建立数学模型,确保最佳直线拟合和传感器线性度的精度,对于传感器的静态特性准确无误地反映被测量的真值,具有重要意义。

2 直线拟合对传感器的线性度影响

表1是笔者从某公司生产的S-250型差动电阻式应变计的标定试验中提取的多次测量进、回程平均值实验数据,旨在通过这一个具体实例分析说明传感器的线性度与直线拟合的方法有关。下面着重介绍三种目前常用的拟合方法。

表1 S-250型差动电阻式应变计一组实验数据

表2 输入值与端点直线拟合输出值

2.1 端点直线拟合的线性度分析

端点直线法:以传感器的校准曲线两端点间的连线作为拟合直线,这种方法很简单,但Δ Lmax也很大。

端点直线拟合是指把传感器多次重复测量的实测数据的起始输出平均值和满量程输出平均值对应的点连成的直线作为传感器的拟合直线的方法。根据这一原理,本实验拟合直线应为连接点(-1000,9669)和(600,10357)的直线。

由式(2),推导

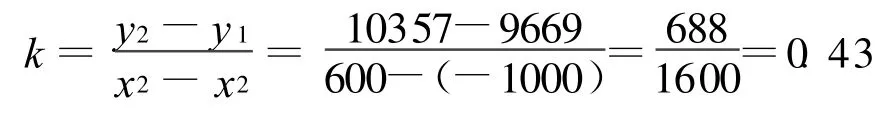
于是求得端基直线拟合的方程为:

y=10099+0.43x

b=y-kx=9669-0.43(-1000)=10099

将各输入值代入可得理论拟合直线各点数据,见表2。

经计算比较有:对应输入值200(10-6)时,在回程有最大偏差Δ Lmax=5,

故线性度:γL=±0.7267%

2.2 最小二乘法直线拟合线性度分析

最小二乘法,这种方法按最小二乘原理求取拟合直线,该直线能保证传感器校准数据的残差平方和最小。最小二乘法的拟合精度很高,但校准曲线相对拟合直线的最大偏差绝对值并不一定最小,最大正、负偏差的绝对值也不一定相等。

如用y=b+kx表示最小二乘法拟合直线,式中的系数b和k可根据下述分析求得。设实际校准测试点有n个,则i个校准数据yi与拟合直线上相应值之间的残差为 △i=yi-(b+kxi),按最小二乘法原理,得到最小二乘法拟合直线方程(推导过程略):

经计算,本实验测量次数为n=9,算得k=0.429,b=10096.9。

于是求得最小二乘法拟合的方程为 :y=10096.9+0.429x将各输入值代入式(4)可得理论拟合直线的各点数值,如表3。

表3 输入值与最小二乘法直线拟合输出值

表4 输入值与输出值之间的偏差

经计算比较有:对应量程输入在点600(10-6)时,有最大偏差 Δ Lmax=2.7,

故线性度γL=±0.3924%

2.3 最佳直线拟合的线性度分析

最佳直线法:该方法以能保证传感器的正反行程校准曲线对它的正、负偏差相等并且最小,由此所得的线性度称为“独立线性度”。通常情况下,“最佳直线”只能用图解法或通过计算机解算来获得。当校准曲线(或平均校准曲线)为单调曲线,且测量上、下限处之正、反行程校准数据的算术平均值相等时,“最佳直线”可采用端点连线平移来获得。

本次实验中测量上下限处正反行程校准数据值相等,因此可以采用最佳直线法求解传感器的线性度。

这里采用求关于最佳直线的方法之一 ——图解法[3],图解法较为直观,可以手算。

首先找出试验数据的端基直线:y=10099+0.43x,各校准点对此端基直线的偏差如表4。

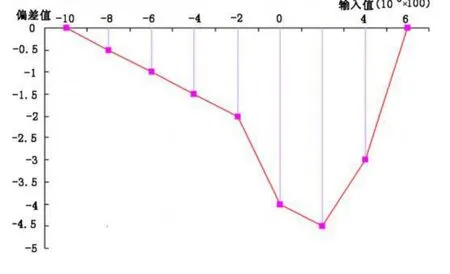
图1 偏差点组成的凸多边形

其次,为了便于作图,将各输入值缩小100倍,将各偏差点标在直角坐标纸上,并由这些偏差点作一凸多边形,即把全部偏差点不是包容在凸变形之内,就是置于凸多边形的各边之上,如图1所示。

然后,由凸多边形的各顶点向其对边引铅垂线(平行于纵坐标轴的直线)。

在凸多边形内的最长一根铅垂线所交的对边是由一组数据点中两点的端基直线偏差点的连线构成,两点的连线经平移使最大正、负偏差绝对值相等后,即为最佳直线。

由图1明显可见,偏差点(200,-4.5)到偏差点(-1000,0)、(600,0)的连线的铅垂线最长。这就对应于实际数据点(200,10180.5)到数据点(-1000,9669)、(600,10357)的连线的铅垂线最长,即图1中颜色加深线段所示。

实际数据点的这根最长铅垂线的长度 Δ L=4.5,即为两倍的相对于最佳直线的最大偏差。

最后,求解得:

x1=(-1000+200)/2=-400

y1=(9669+10180.5)/2=9924.75

x2=(200+600)/2=400

y2=(10180.5+10357)/2=10268.75

k=(10268.75-9924.75)/(400+400)=0.43

b=9924.75-0.43×(-400)=10096.75

于是求得最佳直线拟合的方程为:

y=10096.75+0.43x

表5 输入值与最佳直线输出值

表6 三种直线拟合方法比较

符号交替(或交错)出现的相同的最大偏差为Δ Lmax=2.25,相同的最大偏差的交错点组是最佳直线或最佳曲线存在的一个有利判据,这是其他拟合直线或曲线所没有的特点。

计算独立线性度为:γL=±0.3270%

3 三种直线拟合方法对传感器线性度影响的比较

通过对差动电阻应变计的标定数据的分析可以看出,直线拟合方法不同,传感器线性度也不同,特别是线性差的传感器,尤为突出。比较见表6。

通过前面讨论可以看出,线性度是利用实验测量的数据,以一定的拟合直线或理想直线为基准直线算出来的,直线拟合的方法不同,基准直线就不同,线性度的精度就不同。

4 结 语

在由传感器构成的测量系统中,直线拟合的方法直接决定了线性度的高低,特别是传感器非线性比较明显时,直线拟合的方法直接决定测量系统的准确度。

因此,在测量系统的组建中,若测量系统线性度和精度要求不高,拟合尽量简单,若测量系统线性度和精度要求高,直线拟合最好采用最佳直线法。目前,在传感器测量领域,为了对系统进行有效的补偿从而获得较精确的测量结果,利用计算机对测试的信号通过软件计算,采用多次拟合等计算方法分析系统线性度,是目前传感器直线拟合分析线性度研究的发展方向之一。

[1]常健生.检测与转换技术[M].北京:机械工业出版社,2000

[2]郁有文,常健编著.传感器原理及工程应用[M].西安:西安电子科技大学出版社,2000

[3]孙德辉等.GB/T 18459-2001传感器主要静态性能指标计算方法[S].北京:中国标准出版社,2001