基于神经网络的燃料电池发动机风机系统建模

明 宏，全 睿，全书海，

(1．武汉理工大学自动化学院，湖北 武汉 430070;2．武汉理工大学汽车工程学院，湖北 武汉 430070)

能源与环境问题的日益恶化，发展新能源和替代能源成为了必然选择。质子交换膜燃料电池(PEMFC)由于能量转化率高、功率大、供电时间长、低噪声和无污染等一系列优点，以燃料电池发动机作为动力源成为各国燃料电池汽车的研究热点［1］。影响燃料电池发动机性能的重要单元之一是空气供给系统，评价燃料电池发动机的效率在于辅助系统消耗功率的大小，这些都与风机系统密不可分。为了提高燃料电池发动机的动态性能，保证其稳定可靠运行，对空气供给系统的优化控制是十分必要的，而要对其进行控制，无论是使用经典控制理论还是现代控制理论都需要建立其精确的模型。目前，建模的方法主要有机理建模和辨识建模，在进行机理建模时，通过建立数学方程(微分方程、差分方程或状态空间表达式等)进行其特性描述。作为空气供给系统的核心组件，风机系统的输入输出特性涉及到机、电和流体力学等学科知识，其组成单元之间具有非线性和强耦合性，要建立其准确的动态机理模型具有一定难度，因此，对其进行辨识建模是较好的选择。

神经网络可以任意精度逼近任意连续有界非线性函数［2］，此外，神经网络还具有很强的模式识别和自学习能力，可以实现那些难以用数学模型表示的复杂映射关系，在解决高度非线性系统的模型辨识和控制方面具有巨大的潜力。笔者以武汉理工大学自主研发的60 kW车用燃料电池发动机为研究对象，针对其空气供给系统中的风机建模时试图绕开风机系统内部的复杂性，以风机给定转速和输出压力为输入，以空气流量为输出，利用实验数据将神经网络方法用于其建模，以作为整个空气供给系统建模与优化控制的基础。

1 燃料电池发动机空气供给系统

所设计的燃料电池发动机中，其空气供给系统结构如图1所示。大气首先经过空气过滤器，被高速旋转的风机将空气压缩进入PEMFC空气供给管道，依次经过空气压力调节器、空气压力传感器和空气流量传感器进入燃料电池电堆中。在电堆的入口处，通过控制加湿器对其进行加湿使反应更加充分，在阴极入口处的相对湿度传感器，用来测试空气的相对湿度。根据燃料电池的电化学反应机理［3］，燃料电池系统在进行工作时所需供应的空气质量流量Qam为:

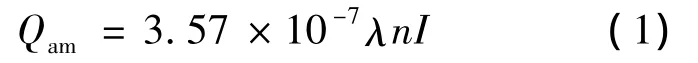
式中:λ为空气过量系数，为了保证反应充分进行，考虑到系统的效率，通常取λ为2左右;I为电堆电流;n为单片电池数。

Qam除以空气密度就可以得出实际所需的体积流量。在实际应用中，控制器根据电堆电流、压力传感器和空气流量计的数据，随时调整风机转速和空气压力，从而控制空气的进气量，达到优化的目的。因此，建立风机系统的模型，根据反应所需的空气流量进行风机转速控制是十分必要的。

图1 燃料电池发动机空气供给系统结构图

2 风机系统的神经网络建模

2．1 风机系统的神经网络辨识结构

图1中的风机系统由马达、风机控制器和两倍转速比的风头组成，由于马达本身是一个强耦合非线性系统，加之风机出口的流量和转速、压力存在一定的非线性关系，因此，建立其精确的动态机理模型很费力，并且其机理模型表达式过于复杂，很难用于控制系统的设计，特别是在在线控制中，无法满足实时控制的要求。由于人为的原因，对其进行机理建模时难免对系统参数进行某些理想化假设，所建立的模型难以保证较高的精度，也不能对多组试验数据进行深入地分析与研究。因此，综合上述神经网络的自学习和自适应能力强的优点，笔者采用BP神经网络对风机系统进行辨识建模，其神经网络辨识结构如图2所示。

图2 风机系统的辨识结构

模型的辨识要求是在给定不同的转速和压力下，能够动态地模拟风机出口空气流量的变化轨迹，完成模型的输入矢量到输出矢量的动态非线性映射。因此，辨识模型可用非线性方程来描述:

利用神经网络进行辨识，就是根据实际测试中的转速V、压力P和流量Fout进行学习和训练，保证误差e最小。

考虑到3层前馈网络可以逼近任意非线性函数，笔者选取3层BP网络对风机系统进行辨识，3层包括输入层、隐层和输出层。显然，输入层有2个节点，即供给管道压力和风机转速，输出层有1个节点，即输出为风机出口风量，隐层中节点数的确定较复杂，往往需要根据设计者的经验和多次实验来确定，因而不存在一个理想的解析式来表示。隐层节点数与问题的要求、输入、输出单元的数目有直接关系。隐层中节点数太多会导致学习时间过长、误差不一定最佳，也会导致容错性差。因此一定存在一个最佳的隐单元数，笔者根据Kolmogorov定理［4］确定隐层节点数:

式中:n为输入单元数;m为输出神经元数;a为［1～10］之间的常数。

2．2 神经网络的学习算法

对于前向网络，标准BP算法是一种很实用的算法，它通过调整网络权值和阈值能达到网络的输出与目标输出之间误差平方和最小。其权值调整的算式［5］为:

多层前向神经网络通过不断调整网络中各神经元相应的连接权和阈值可以使网络的输出尽可能与期望的输出一致，因而BP算法是一种行之有效的学习方法。但传统的BP算法具有明显的局限性，主要表现为收敛过程慢，且当误差最小值较高时，很容易陷入局部最小值。笔者采用Levenberg－Marquardt(LM)优化算法［6］对上述的 BP算法进行改进:

设X(k)为第k次迭代的权值和阈值所组成的向量，新的权值和阈值组成的向量X(k+1)由式(6)可得:

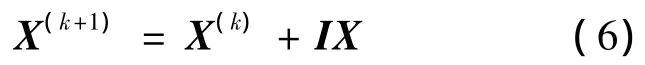
根据牛顿法则［7］，有:

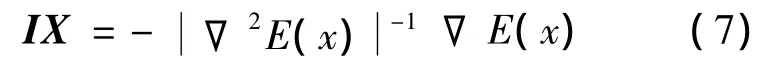
式中:▽2E(x)为误差指标函数E(x)的Hessian矩阵;▽E(x)为梯度。

设误差指标函数为:

式中，e(x)为误差。

进一步可得:

根据高斯－牛顿法则，有:

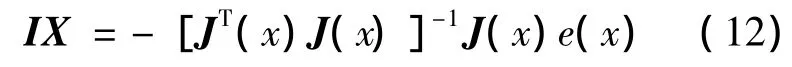
由LM算法:

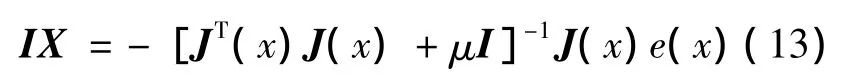
式中:μ为大于0的常数;I为单位矩阵。

当μ=0则为高斯－牛顿法，如果μ取值很大，则LM算法接近于梯度下降法，每迭代成功一步，则μ减小一些，这样在接近误差目标时，逐渐与高斯－牛顿法相似。而高斯－牛顿法在接近误差最小值时，计算速度更快，精度也更高，由于LM算法利用了近似的二阶导数信息，因此它比梯度下降法提高速度几十甚至上百倍。

3 基于神经网络的风机系统辨识结果

所用的无刷直流电动机参数为:Umin=290 V，Umax=400 V，Imax=70 A，nmax=15 000 r/min，Rs=0．17 Ω，Ls=0．23 mH，ke=18 V/kr/m，np=5，Lm=0．03 mH，km=0．17 N/A。所建立的风机神经网络模型其实验数据由湖北省燃料电池重点实验室测得，共有200组，基于篇幅所限，笔者仅给出风机转速、空气供给压力差和空气流量的部分数据，如表1所示。

该风机的神经网络模型使用函数newff()建立BP网络，隐层神经元数目选为7比较合适，隐层采用传输函数分别为双曲正切S型tansig，训练函数采用基于上述LM算法的trainlm函数。设定训练误差指标为0．000 2，训练步数设为1 000，学习速率为0．1，网络训练误差如图3所示，可见经过16步训练即达到要求。部分仿真程序如下:

a=［x］';%风机转速

b=［y］';%空气压力

c=［z］';%空气流量

p=［a;b］;

t=［c］;

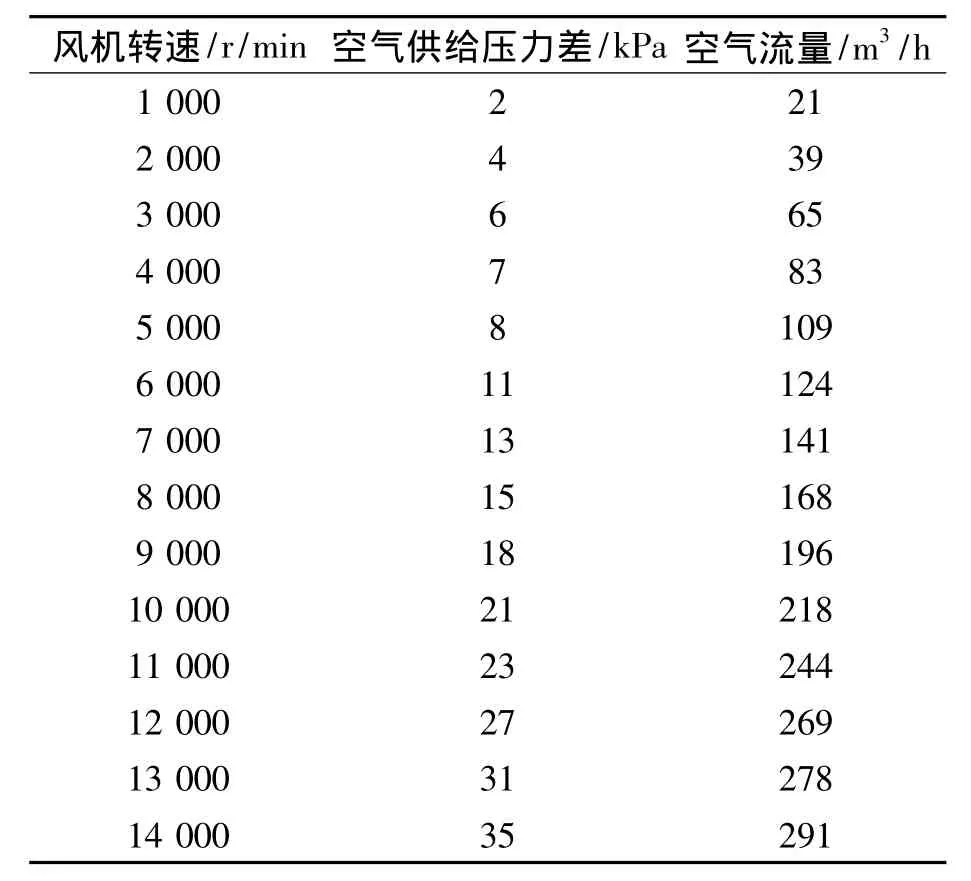
表1 风机测试的部分数据

图3 利用LM算法的神经网络训练误差

for i=1:2

P(i，:)=(p(i，:)－ min(p(i，:)))/(max(p(i，:))－ min(p(i，:)));%输入量归一化

end

T(1，:)=(t(1，:)－ min(t(1，:)))/(max(t(1，:))－min(t(1，:)));%输出量归一化

threshold=［0 1;0 1］;

net=newff(min max(P)，［71］，{'tansig'，'logsig'}，'trainlm');

net．trainParam．epochs=1 000;

net．trainParam．goal=0．000 2;

net．trainParam．lr=0．01;

net=train(net，P，T);

Y=sim(net，P);

保持上述设置不变，利用普通梯度下降法进行神经网络训练，其误差曲线如图4所示，由图4可知，经过1 000步之后都未能收敛，可见，笔者所选用的LM算法收敛速度明显比普通梯度下降法快。

为了验证所建立的风机系统神经网络模型的准确性，利用命令plot(Y－T)将上述训练好的神经网络对训练样本中不同转速和空气压力条件下的空气流量预测值与实际值进行比较，预测误差曲线如图5所示，可见训练好的神经网络模型能以高精度逼近样本复现的数据。

图4 利用梯度下降法的神经网络训练误差

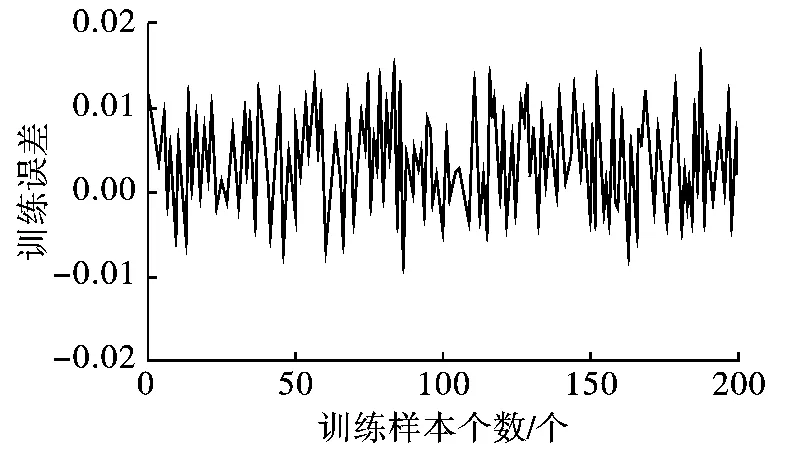
图5 训练误差

为了进一步验证风机系统神经网络模型的泛化能力，现场通过燃料电池发动机主控制器［8］改变风机的转速，同时调节调压阀的压力，测得空气流量值，然后利用转速值和压力值输入到训练好的神经网络并进行反归一化得到空气流量的预测值，对比结果如图6所示。

图6 不同转速和空气压力下的对比结果

可见，建立的风机系统神经网络模型对不同于训练样本的数据仍然具备较强的预测能力，因此，建立的风机系统神经网络模型具有较好的泛化能力，也是有效的。在对空气系统做进一步的建模和仿真时，只需在Matlab命令窗口中，用函数gensim()生成经过训练的BP神经网络模型，将其加入空气供给控制系统的Matlab/Simulink模型中即可进行各种控制策略的仿真和验证［9－10］。

4 结论

以上辨识过程表明，采用神经网络辨识的方法实现风机这类非线性系统的建模是完全可行的，建模的精度也比较高，不仅能对训练样本中的数据进行预测，而且对偏离训练样本中的数据具有较强的泛化能力。最重要的是它避开了复杂的解析建模过程和复杂的非线性微分方程组描述的模型，使非线性系统的输入输出特性能快速得到，为燃料电池发动机的空气供给系统实时控制，特别是在线优化控制创造了条件。它虽然不能像解析模型那样有非常清晰的物理意义，但却能有效地表达风机系统输入输出的非映射关系。

［1］ 陈全世，齐占宁．燃料电池电动汽车的技术难关和发展前景［J］．汽车工程，2001，23(6):361 －364．

［2］ NARENDRA K S，PARTHASARATHY K．Identification and control of dynamical systems using neural networks［J］．IEEE Transactions on Neural Networks，1990，1(1):4－27．

［3］ LARMINIE J，DICKS A．Fuel cell systems explained［M］．Chiechester:John Wiley＆ Sons，2002:54－68．

［4］ 葛哲学，孙志强．神经网络理论与Matlab R2007实现［M］．北京:电子工业出版社，2005:100－300．

［5］ 徐礼超，马从兵，范钦满，等．基于BP神经网络的汽车发动机故障诊断方法研究［J］．拖拉机与农用运输车，2007，34(6):101 －102．

［6］ 赵弘，周瑞祥，林廷．基于Levenberg－ Marquardt算法的神经网络监督控制［J］．西安交通大学学报，2002，36(5):523 －527．

［7］ 阮晓钢．神经计算科学［M］．北京:国防工业出版社，2006:23－65．

［8］ 全书海，王超，宋娟．车用燃料电池发动机控制系统与协调控制研究［J］．华中师范大学学报:自然科学版，2005，39(3):325 －327．

［9］ 全书海，张天贺，张立炎．PEMFC空气供应系统的建模、仿真与控制［J］．武汉理工大学学报:信息与管理工程版，2007，29(10):61 －64．

［10］ 刘洋，全书海，张立炎．燃料电池发电系统温度控制策略研究［J］．武汉理工大学学报:信息与管理工程版，2010，32(2):268－272．