基于虚拟仪器的车辆传动系统扭振测试与分析

周 斌，赵光明，陈 雷

(武汉理工大学机电工程学院，湖北 武汉 430070)

对于典型的发动机前置后轮驱动的车辆，发动机的输出动力依次经过传动系统中的离合器、变速箱、万向节、传动轴、主减速器、差速器和半轴，最后传递到车轮。这些具有弹性和转动惯量的部件，在传递动力的同时也传递了发动机产生的扭振［1］。当扭振的频率与传动系统的固有频率相近时，会在部件上产生很大的附加应力，引起冲击和振动，激发强烈的噪声，严重时甚至会引起连接件的损坏和回转件的扭转疲劳断裂，导致动力传递的中断［2］。这不仅影响车辆的平顺性和舒适性，还会带来行驶的安全问题。

1 扭振分析与测试

在旋转轴系中，扭振信号的频率与转轴的转速密切相关，仅研究绝对振动频率不可能全面反映轴系的扭振状况，应找出该振动频率是在何种转速下产生的，从而使轴系在工作时尽量避开共振转速区，避免系统发生扭转共振。

车辆在实际工作中，总是处于不断变速的工况下，此时旋转轴系的扭振信号属于时间域内非平稳随机信号，由于不满足傅立叶变换对信号的平稳性要求，不适合用传统的频谱分析方法进行分析［3－5］。为解决这个问题，产生了阶比分析的方法。阶比(又称作阶次)可定义为信号振动频率与回转基频的比值［6］，即:

式中:fv为信号振动频率;fc为回转轴的基频。

在阶比分析中，关键是对回转基频(或轴的转速)进行跟踪，使信号的采样频率能够随回转基频的变化而调整。即无论轴系转速如何变化，信号的采样值只与轴上的角度位置有关［7］，其实质是等角度的采样方法。此时，扭振信号就由时域内非稳定信号变成了角度域内的周期平稳信号，从而可以用传统的信号频谱分析方法对角度域内的扭振信号进行分析。

在扭振测试中，常采用非接触式测量法。安装于轴上的测试齿盘的每一个轮齿经过电涡流传感器时，会在传感器中感应出方波形式的交变信号。当轴连续转动时，传感器获取一系列的方波信号，信号的疏密程度与轴的角速度变化有关，因此蕴含了轴的扭振信息。而每一个方波对应一个转过的轮齿，即实现了扭振信号的等角度采样。再通过两次仪表对等角度采样，信号按照周期进行截取、处理和分析后，即可获得轴系的扭振。

依据采样定理可知，采样频率fs只有理论上≥最高频率fmax的2倍时，才能保证原始信号中的信息不会因采样而丢失。实际中，为避免产生频谱混淆，采样频率fs要求为系统最高估计频率的5～10倍以上。在研究中，测试齿盘的齿数为N，轴的转速为ni，则信号的采样频率fs=N×ni/60。而轴系的扭振由多次谐波组成，一般分析到12谐次即可保证精度，即在某一转速下所需研究的扭振最大频率为 fmax=12×ni/60，因此，齿盘齿数N=(5～10)×12=60～120齿即可。

2 扭振实验台与测试系统

2．1 实验台搭建与建模

在扭振研究中，搭建实验台进行扭振测试是一个重要环节。它可以忽略诸多不确定因素的影响，易于分析出传动系统扭振的内在规律。以某型直列4缸柴油发动机前置后驱中型车动力传动系统为研究对象，搭建的车辆传动系统扭振实验台如图1所示。图中圆圈处为测试齿盘布置位置。

图1 扭振实验台

若不考虑阻尼的影响，可将上述发动机至传动系统简化为由若干集中质量和刚度环节所组成的扭振模型。变速器在不同挡位下的集中质量模型略有不同，在此，仅列出变速器位于二挡时，发动机和传动系统简化成的15质量无阻尼扭振模型，如图2所示。

图2 二挡时的扭振模型

在图2中，J1、J2为发动机自由端皮带轮和减振器转动惯量;J3～J6为发动机气缸转动惯量;J7、J8为主飞轮、次级飞轮和离合器转动惯量;J9s～J11s为变速器各挡位下啮合齿轮的转动惯量;J12～J15为传动轴部件、飞轮组部件和测功机的转动惯量;K1、K2为橡胶减振器、曲轴自由端扭转刚度;K3～K5为曲拐1、2、3 的扭转刚度;K6～ K8为曲轴飞轮端、双质量飞轮和变速器输入轴的扭转刚度;K9s～K11为变速器各挡位中间轴以及输出轴的等效扭转刚度;K12、K13为传动轴扭转刚度;K14为电涡流测功机传动轴扭转刚度。

对该无阻尼扭振模型，利用模态分析法进行系统的扭振固有频率计算，其公式为:

式中:K为刚度矩阵;J为转动惯量矩阵;A为角位移矢量。

代入各部分的转动惯量和刚度的数值，计算出二挡工况下的前8阶扭振固有频率如表1所示。

表1 二挡时前8阶固有频率

2．2 扭振测试系统

虚拟仪器是电测技术与计算机测控技术的结合，随着虚拟仪器技术的不断发展，其强大的优势在越来越多的试验测试中体现出来［8－10］。笔者基于虚拟仪器技术的开发平台，设计出基于PC的DAQ(data acquisition)系统。系统主要由传感器、测试硬件和软件3个部分组成。

传感器采用台湾超荣公司的CTS－A12M－2ANA电涡流传感器，该传感器能将信号的获取与整形整合处理，形成开关量的形式输出。测试硬件的核心是NI公司的PXI6259 M系列数据卡，该卡是一种基于PC的测量和自动化平台，能对信号进行采集和预处理，并将数字化的信号经过总线传输给计算机。通过编制相应的扭振测试软件，对获取的等角度采样信号进行整周期截断，对周期内的方波信号进行离散傅立叶变换，运用转速跟踪算法和阶比分析方法，实现对扭振信号的处理与分析。

3 实验测试与分析

3．1 实验测试

发动机启动并运行稳定后，将变速器经空挡、一挡切换到二挡，通过油门控制器使发动机在800～1 360 r/min的范围内稳定升速。二挡传动比i=2．318，此时传动轴的转速为345～585 r/min。

通过将传感器获得的每个方波信号历经的时间转换为转过每个轮齿时的瞬时角速度，可以获得升速阶段的瞬时转速图，如图3所示。

图3 瞬时转速图

在图3的瞬时转速数据中，以传动轴每转两转为一个整周期，采用转速跟踪算法计算出各个整周期内的平均转速。跟踪提取的20处平均转速 (r/min)为:345．238，345．715，345．958，363．306，374．454，389．035，406．727，407．010，421．769，425．275，425．539，441．530，453．845，474．510，483．269，527．940，532．621，555．024，575．074，578．157。

在每个整周期中，采用离散傅立叶变换及频谱分析方法，运行编辑程序，得到传动轴在该转速下的阶比－幅值谱。综合生成该20处的阶比－转速－幅值谱瀑布图，如图4所示。

图4 二挡下的阶比－转速－幅值谱瀑布图

对瀑布图按照阶比进行切片，可以获得在某一阶比下的转速－幅值谱图。0．5～2．0阶比的转速－幅值谱图如图5和图6所示。

图5 二挡下的0．5和1．0阶频谱图

3．2 扭振分析

系统的固有频率为f0时，对应的发动机共振转速为 nc，nc=60 ×f0/order。

在二挡时，变速器的速比i=2．318，发动机和传动轴的共振转速如表2所示。

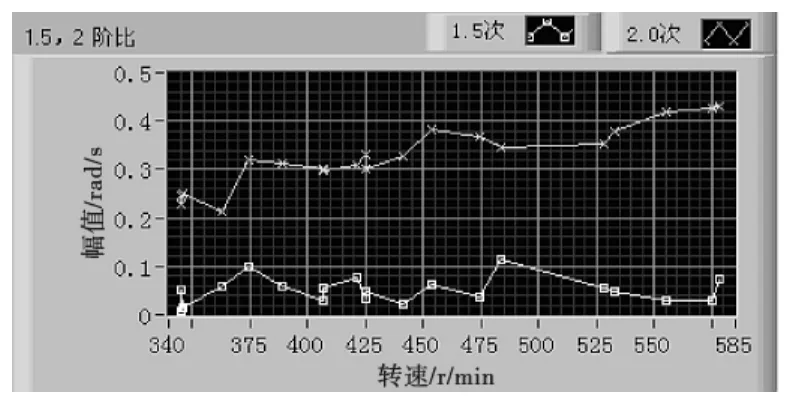
图6 二挡下的1．5和2．0阶频谱图

表2 共振转速表

从表2中可知，理论计算得出的传动系统在1阶、2阶、4阶以及4阶以上振动的共振转速均不在传动系统实际工作转速345～585 r/min范围内，不可能通过测试检测到扭转共振;仅当传动系统在3阶振动时，其1阶比的共振转速473．7 r/min位于实测范围内，会有扭转共振发生。

在阶比谱中，共振转速ni为曲线峰值所对应的转速nk与阶比K的乘积，即:

在图5和图6中，虽然存在多个峰值，但是经式(3)计算，只有一处与理论值接近:在1阶比时，有一峰值转速为475 r/min(图中圆圈处)，其共振转速n1=1．0×475=475 r/min，相对理论共振转速为 473．7 r/min，误差为 0．27%。

这表明在二挡加速过程中，当传动系统的转速经过n0=473．7 r/min时，系统会产生1阶比的扭转共振。

3．3 对比验证

采用东南大学研发的ANZT10扭振测试仪在相同的工况下进行测试。在此，仅列出1阶比的转速－阶次－幅值谱图，如图7所示。图5与图7相比，图5中纵坐标为扭振角速度，而图7中纵坐标为扭角。此外，图5中仅列出升速过程中所跟踪的20处转速，因而形成的曲线轮廓与图7中曲线略有差别。

图7 1阶比转速图

由图7可知，在1阶比时，有一峰值转速为472 r/min(图中圆圈处)，其共振转速n1=1．0×472=472 r/min，相对理论共振转速为 473．7 r/min，误差为 0．36%。

经测试结果的对比，说明在二挡升速过程中，经过473．7 r/min附近的共振区，传动系统会发生较大的扭转共振。

4 结论

针对车辆传动系统的扭振问题，以搭建的发动机－传动系统扭振实验台为研究对象，建立了无阻尼扭振模型，并对系统在二挡时的扭振固有频率进行了理论计算。运用阶比分析的方法，结合转速跟踪和等角度采样技术，以虚拟仪器作为测试与分析平台，对二挡工况下传动系统升速过程的扭振进行实验测试与分析，结果表明实测值与理论值吻合较好。经与东南大学的扭振测试仪的测试结果对比，验证了传动系统在实验转速范围内发生了扭转共振，从而为传动系统的设计改进和扭转共振的降低提供了参考依据。

［1］ 陈家瑞．汽车构造［M］．北京:机械工业出版社，2005:18－102．

［2］ 舒红宇，张伟伟，雷宝云．路面激励下汽车传动系统的随机扭转振动分析［J］．解放军理工大学学报:自然科学版，2009(1):87－91．

［3］ 朱继梅．非稳态振动信号分析［J］．振动与冲击，2000(1):86－87．

［4］ 栾军英，康海英，郑海起，等．基于阶次跟踪的旋转机械启动过程振动分析［J］．军械工程学院学报，2005(2):23－25．

［5］ LU Z H，CHEN T．Design and analysis of a dual mass flywheel－circumferential spring torsional damper［C］//Proceedings of the Eleventh Intemational Pacific Conference on Automotive Engineering．Shanghai:［s．n．］，2001:536 －539．

［6］ 傅俊庆，廖坤鹏，沈中伟．旋转机械振动信号角域与时域采样方法的对比研究［J］．长沙交通学院学报，2007(1):75－80．

［7］ 杨炯明，秦树人，季忠．旋转机械阶比分析技术中阶比采样实现方式的研究［J］．中国机械工程，2005(3):249－253．

［8］ 丁士心，崔桂梅．虚拟仪器技术［M］．北京:科学出版社，2005:28－87．

［9］ 王晓，韩焱，毛晚堆，等．发动机性能虚拟仪器测试系统设计［J］．微计算机信息，2008(7):62－64．

［10］ 应怀樵．虚拟仪器与计算机采集测试分析仪器的发展和展望［J］．测控技术，2000(8):4 －6．