高速铁路无砟轨道桩板结构路基动力特性研究

2011-04-27李保俊马坤全张欣欣

石家庄铁道大学学报(自然科学版) 2011年1期

李保俊，马坤全，张欣欣

(同济大学桥梁工程系，上海 200092)

0 工程背景

本桩板结构路基位于某高速铁路K30+951.5～DK31+115.085段，每只托梁下布置两根Φ1250 mm钻孔灌注桩，桩长45.0 m，托梁上接两块承载板，每块承载板厚1 m，宽4.4 m，每跨长10 m，三跨一联，详见图1、图2。此工点的地质状况见表1(表中，h1为土层顶面标高;h2为土层底面标高)。

1 实测数据

采用余振法测取桩板结构路基的动力特性，实测此工点桩板结构路基的横、竖向自振频率分别为1.3428 Hz和3.1738 Hz，图3～图6分别表示工点1桩板结构路基实测典型横、竖向振动余振波形及其对应的功率谱。

图1 桩板结构横断图(单位:m)

表1 本桩板结构经过的地质状况

2 m法计算结果

以往工程上应用m法考虑桩土相互作用的具体做法是:利用m法算得桩顶等效刚度，在乘以一个1到3的系数作为动静刚度比作为结构的弹性边界来计算结构的自振特性［1］。先运用此法计算桩板结构的自振特性:动静刚度比分别取1.5、2、2.5、3，对各层土m值分别取最小，平均和最大值计算得桩顶等效刚度，得到此桩板结构一阶横向刚体平动的频率为4.162～8.923 Hz，一阶竖向刚体平动的频率为14.891 ～27.842 Hz。

3 提出的数值模拟方法

3.1 计算模型

图2 桩板结构侧面图(单位:m)

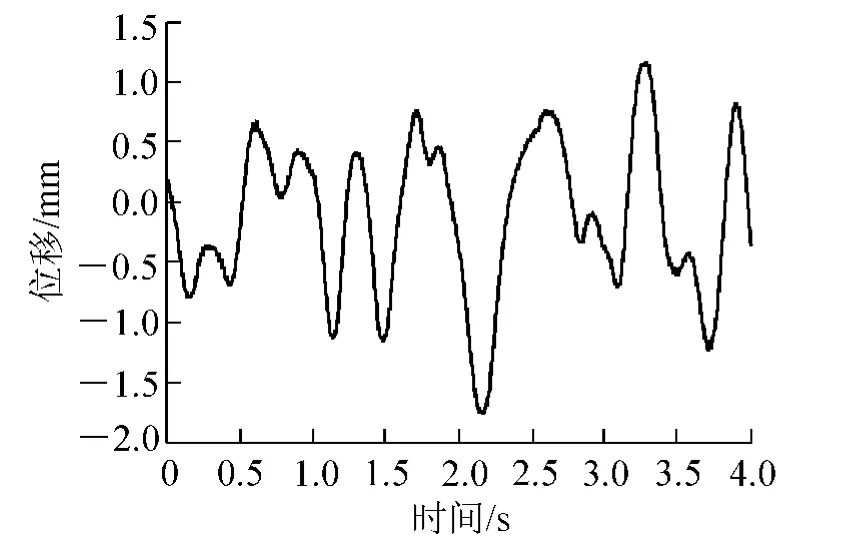
图3 实测横向振动时程样本典型曲线

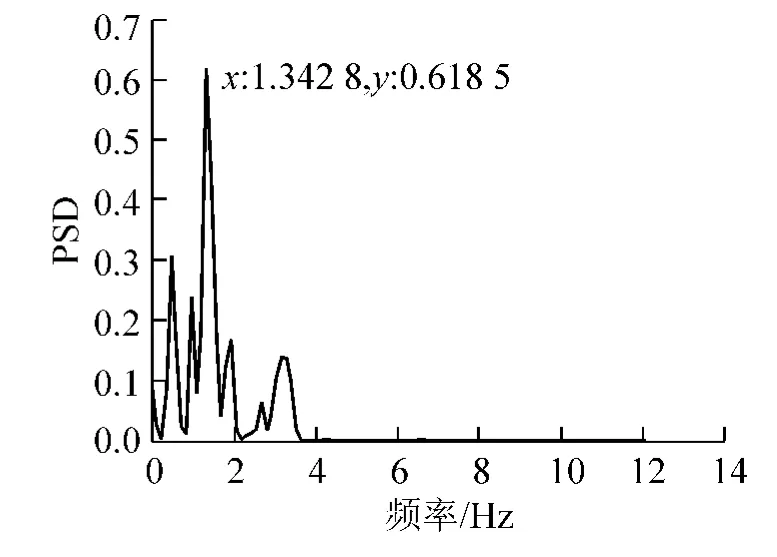
图4 实测横向振动功率谱典型曲线

图5 实测竖向振动时程样本典型曲线

图6 实测竖向振动功率谱典型曲线

针对工点1桩板结构路基，采用国际通用大型结构有限元分析软件Ansys，以实体单元建立土-桩基-结构系统振动的三联桩板结构路基动力特性分析模型(图7、图8)。其中，承载板厚1.0 m，长 10.0 m，宽 4.4 m;托梁长 10.0 m，宽1.6 m，高1.5 m。在桩板结构两端支点位置，通过耦合承载板与托梁接触面上的节点在竖向和横向的平动自由度(主从节点法)模拟承载板和托梁的铰接状态，而托梁与桩基(桩基直径1.25 m范围内)则共用其相接触的节点模拟托梁与桩基的固结构造特性;在桩板结构中支点位置，通过共用桩基、托梁及承载板相接触的节点(桩基直径1.25 m范围内)来模拟承载板、托梁和桩基的固结状态。桩长45 m，直径1.25 m，桩基横断面划分24个单元(参见图9)。计算模型所取土体范围为:竖向取至桩底以下20 m，横向沿桩板结构左右两侧边界各外伸65 m，纵向沿桩板结构前后两端边界各外伸4.2 m，即整个模型为:65 m(竖向)×140 m(横向)×100 m(纵向)。假定桩土间变形协调，即通过共用节点的方式来模拟桩土间的连接。模型底面土体节点假定为固结，其它边界处假定为自由，鉴于本研究不讨论桩板结构路基的纵向振动，为节约计算时间，不失一般性，限制所有节点的纵向位移。整个分析模型共有73090个节点，62240个单元，其中承载板单元8460个，托梁5280个，桩基4800个，土体43520个。

3.2 主要计算参数

承载板及托梁均为钢筋混凝土结构，考虑到混凝土的弹性模量在多次重复荷载作用后降低约20% ～25%，因此，承载板及托梁的弹性模量取为0.8 E=2.72×104MPa;桩板结构路基上的二期恒载作为质量施加到承载板中，承载板的等效质量密度取为2600×1.3273=3451 kg/m3，泊松比为0.2;桩基也为钢筋混凝土结构，其弹性模量取为0.8 E=2.64×104MPa;托梁及桩基的质量密度均取为2600 kg/m3;泊松比为0.2。土体的物理力学参数按照土体的种类和埋深进行分类，详见表2，其中平均剪切波速参考文献［2］，密度和泊松比取自文献［3］，根据G=ρv2得到最大剪切模量［4-5］，由E=2G(1+μ)得到换算弹性模量，动弹模取为静弹模的 2.2 倍［6］。

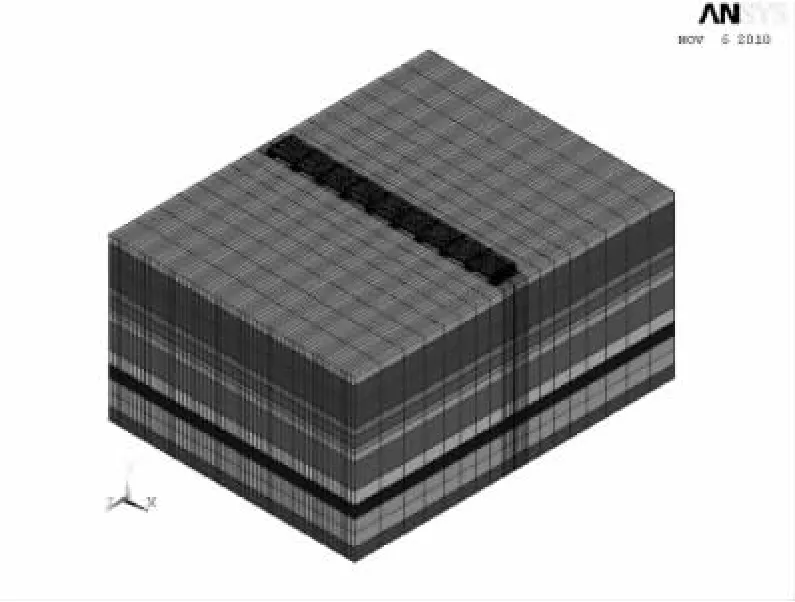
图7 桩板结构有限元模型(整体)

图8 桩板结构有限元模型(局部)

图9 桩以及其周围土体的划分

表2 有限元计算所用土体材料参数

3.3 计算结果

采用土体-桩基-托梁-承载板结构模型计算的桩板结构路基前15阶自振频率如表3所示，图10、图11分别为桩板结构路基一阶横向和竖向刚体平动振型。

综合表3及图10～图11可知，采用土体-桩基-托梁-承载板结构模型计算桩板结构路基动力特性，其前15阶主模态均以土体振动为主，板(承载板)梁(托梁)结构基本上呈现由土体振动所带动的刚体运动;桩板结构路基横、竖向基频分别为1.3742 Hz和3.0695 Hz，土体-桩基-托梁-承载板系统横向刚度低于竖向刚度。因此，桩板结构路基的竖、横向刚度主要由土体与桩基刚度控制，要提高桩板结构路基的整体刚度首先要提高其桩基础的刚度，尤其是其横向刚度;板(承载板)梁(托梁)结构与桩基应有合理的刚度匹配，方可有效发挥其刚度效应。

图10 土体的1阶横向对称振动带动桩板结构横向平动

图11 土体的上下振动带动桩板结构上下振动

表3 桩板结构自振频率及振型描述

4 实测数据与“m”法计算结果、数值计算结果的对比和分析

桩板结构路基自振频率理论与实测值的比较如表4所示。从表4可看出，采用传统的“m”法计算桩基在桩顶的等效刚度，然后再计算考虑基础弹性的桩板结构的自振频率，其计算值与实测值相差较大;而直接建立土体-桩基-托梁-承载板系统有限元模型，考虑土体刚度及质量参与计算所得的桩板结构路基自振频率与实测值比较接近。由此表明，对于桩板结构路基，不宜简单沿用计算桥梁结构自振特性的传统方法，即采用“m”法考虑基础弹性的结构动力特性的影响，而应将土体、桩基、托梁及承载板作为完整的振动系统计算其动力特性。

表4 桩板结构路基自振频率理论与实测值

传统的桥梁结构，一般采用群桩基础，桩基刚度一般情况下比结构自身刚度大，其振动主要由结构刚度控制，基础弹性只是对结构系统刚度起折减作用;但就桩板结构路基而言，每个托梁下只有少数几根桩基，且桩长较短，其桩基刚度远小于传统桥梁结构的群桩基础，且板(承载板)梁(托梁)结构跨度小，刚度大，因此，对于桩板结构路基，其振动主要由基础振动控制，桩基周围土体振动对桩板结构路基系统的振动起着举足轻重的作用，因此，建立土体-桩基-托梁-承载板系统有限元模型，考虑桩基周围土体刚度和质量的振动参与，方能正确计算桩板结构路基的自振特性。