三相电压型PWM整流器的解耦与控制研究

秦静，李世光，蒋正友

（中国矿业大学 信息与电气工程学院，江苏 徐州 221008）

三相电压型PWM整流器的解耦与控制研究

秦静，李世光，蒋正友

（中国矿业大学 信息与电气工程学院，江苏 徐州 221008）

首先给出了三相电压型PWM整流器的拓扑结构并在其基础上对PWM整流器进行了解耦分析。通过静止坐标变换和旋转坐标变换，得到了简化的、有利于控制系统设计的三相电压型PWM整流器的数学模型。当模型不准确或系统参数与模型参数不完全匹配时，基于旋转坐标变换的矢量控制仍然存在解耦控制失败的可能，影响系统的控制性能。为实现可靠、安全的解耦控制，基于感应电动机定子电流解耦控制思想，对三相电压型PWM整流器电流内模解耦控制策略进行了研究，给出了内模解耦控制器的设计及实现方案，并进行了仿真实验。结果令人满意。

多变量系统；解耦控制；内模解耦控制

1 引言

为了提高功率因数，抑制谐波污染，结合PWM（pulse width modulation）技术的新型整流器——PWM整流器倍受关注［1］。这种整流器克服了传统整流器输入电流谐波含量高，功率因数低的缺点，可获得可控的升压型AC／DC变换性能，实现网侧单位功率因数和正弦波电流控制及电能的双向传输。实现PWM整流器三相电压和电流的解耦控制，是近年来学术界关注和研究的热点。对PWM的耦合现象，诸多文献提出了多种不同的解耦控制策略，其中利用旋转坐标变换方法的矢量控制，是一种比较成功的解耦控制策略，但矢量变换后仍存在有功电流分量和无功电流分量之间交叉耦合电势的作用。本文在此基础上对三相电压型PWM内模解耦进行研究并进行了仿真分析，结果令人满意。

2 三相电压型PWM整流器的耦合性分析

图1为三相电压型PWM整流器拓扑结构，假设网侧输入电压为三相对称正弦波电压，输入电感线性不饱和。考虑纯电阻性负载，对于基波分量，在三相静止a，b，c坐标系中，建立采用开关函数描述的数学模型［2］为

图1 三相PWM整流器拓扑结构图Fig.1 The topology structure diagram of PWM

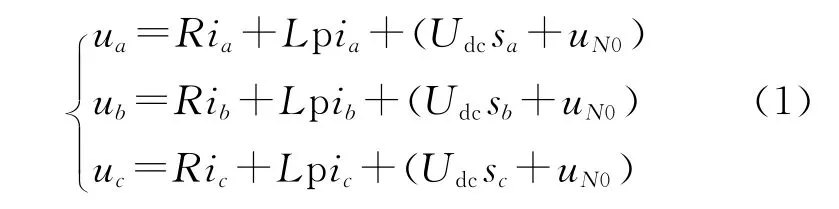
式中：sa，sb，sc为三相静止a，b，c坐标系开关函数；ua，ub，uc为电源侧三相相电压；R为线路电阻与开关管损耗等效电阻之和；p为微分算子。

当si＝1，上桥臂导通，下桥臂关断；si＝0，下桥臂导通，上桥臂关断（i＝a，b，c）。

式（1）为三相电压型PWM整流器的一般数学模型，具有物理意义清晰、直观等特点，但不利于控制系统设计。因此，可通过将三相静止a，b，c坐标系变换到以电网基频同步旋转的d，q坐标系，将前者中的正弦量转化成后者中的直流量，以达到简化控制系统设计的目的，令

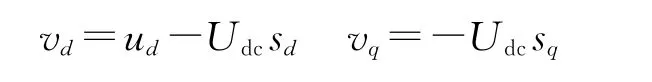
得到三相电压型PWM整流器在两相同步旋转d，q坐标系的数学模型为

式中，sd，sq为两相旋转d，q坐标系开关函数，经坐标变换，简化了PWM整流器模型，将同步旋转坐标系d轴按电网电压矢量定向，电网的q轴分量uq＝0。PWM整流器交流电流矢量的d轴分量为有功分量，q轴分量为无功分量。

图2为PWM整流器交叉耦合图。由图2可见其中存在交叉耦合现象。

图2 PWM整流器交叉耦合图Fig.2 The cross-coupling diagram of PWM

3 三相电压型PWM整流器的解耦控制

在工程实际中，往往由于算法太复杂而难以实现较好的解耦，因而，寻求简单易行的有效解耦方法是目前普遍关注的问题，同时，将各种解耦方法有效融合也是实现解耦的好途径。本文将对PWM的各种解耦方法进行简单的介绍和比较。进而找出方便易行的解耦方法。

3.1 传统解耦方法［3］

3.1.1 前馈解耦

由图2可知d轴和q轴分量间存在交叉耦合，使得两分量不能独立调节。前馈补偿即在输入给定电压中补偿系统产生的耦合电动势，以消除输入交流电流交叉耦合影响，前馈解耦控制原理如图3所示。

图3 前馈解耦原理图Fig.3 The principle diagram of feedforward decoupling

在udq和uqd作用下，d轴与q轴之间的耦合电势得到补偿，PWM整流器被解耦。

当PWM为线路电感的估计值和实际值L相等时，通过前馈解耦，d轴与q轴间的耦合电压可得到消除。解耦后，PWM在d，q坐标系的等效模型为两个独立电压子系统，可以通过PI调节器进行控制。其中d轴电压子系统产生id；q轴电压子系统产生iq。

3.1.2 对角矩阵解耦法

在PWM整流器中，对角矩阵的主对角线元素为PWM整流器的d轴和q轴上的传递函数1／（R＋Ls），由式（2）得：

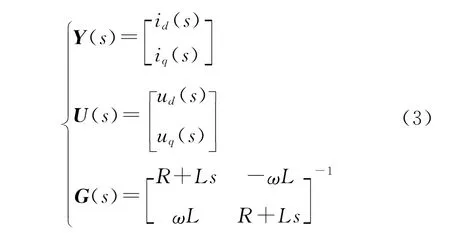
由对角矩阵法解耦的原理得：

由此可得解耦矩阵G1（s）的传递函数为

PWM整流器对角矩阵法解耦的原理如图4所示。

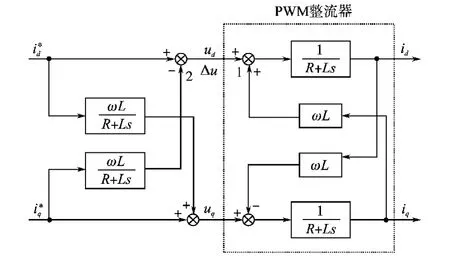
图4 对角矩阵法解耦的原理图Fig.4 The principle diagram of diagonal matrix method decoupling

PWM整流器被解耦。对角矩阵解耦法也存在与前馈解耦法相同的问题。

3.1.3 反馈解耦法

为了克服上述解耦方法的缺点，可将解耦电压项中的给定电流i＊d和i＊q换成实际电流id和iq来实现解耦，即反馈解耦。反馈解耦的去耦项为-和，如图5所示。以PI1，PI2为核心组成电流分量的2个控制闭环，这将有助于电流的动态响应。

图5 反馈解耦原理图Fig.5 The principle diagram of feedback decoupling

图5中，反馈解耦是将PWM整流器的d，q轴电流反馈量用于解耦电压的计算，并将其引入PWM整流器的控制电压输入端进行叠加补偿，以实现PWM整流器交叉耦合电压的解耦。反馈解耦是建立在电流反馈量无延迟和交叉耦合项中的电网电感L的估计值和实际值高度吻合基础上的。然而由于电网中有感性负载，电流滞后于电压；另外，电网电感L会随着负载的运行发生改变，从而与估计值之间产生偏差，使得解耦电压的计算值和交叉耦合电压项实际值之间出现偏差（L-）ωiq和（L-）ωid，使反馈解耦控制效果下降。所以，由于负载参数的变化，反馈解耦也不可能达到完全解耦。

3.2 智能解耦控制

智能解耦方法［4，5］以神经元网络解耦方法为代表。由于神经网络［6］可实现多输入到多输出的映射，以任意精度逼近任意函数，并具有自学习功能，因此适用于时变、非线性、特性未知的对象。目前，神经网络解耦在非线性系统中的应用已有了一些研究成果，但更多的解耦策略带有尝试性，通常依靠大量仿真实验来研究。

神经网络解耦控制系统的结构通常采用以下3种形式：

1）神经网络解耦补偿器置于被控制对象与控制器之间；

2）神经网络解耦补偿器置于控制器之前；3）神经网络解耦补偿器置于反馈回路。

以上解耦方法在理论上是成立的，但是在实际的控制系统中应用难度很大，其主要问题是解耦器的设计依赖被控对象的数学模型，要求被控对象的数学模型已知且为线性时不变。多变量的控制系统，由于回路之间的耦合，数学模型就比较复杂，且参数的测量和计算就比较复杂，这样则导致解耦器和控制器无法设计。为了克服解耦效果依赖于被控对象准确数学模型的不足，可寻求一些对模型精度要求不高的智能解耦方法。内模控制IMC（internal model control）不过分依赖于被控对象的准确数学模型，对模型精度要求低，工程上容易实现，是一种先进控制技术。

4 三相电压型PWM的内模解耦控制

4.1 内模控制的基本结构

所谓内模控制，其设计思路就是将对象模型与实际对象相并联，控制器逼近模型的动态逆，内模控制器取为模型最小相部分的逆，并通过附加低通滤波器以增强系统的鲁棒性，其基本结构图如图6所示。

图6 内模结构图Fig.6 The block diagram of IMC

图6中，R（s）为给定值；CIMC（s）为内模控制器；Ym（s）为内模输出；D～（s）为系统输出Y（s）与内模输出Ym（s）之差；G（s）为内模控制对象。

导致柴油机活塞熔顶主要因素有如下几点：活塞顶部严重积炭；活塞环胶结或断裂；供油不均；喷油嘴工作不良；柴油机产生爆震；机油冷却喷嘴堵塞；柴油机长时间超负荷超速运行，或柴油机散热不良；活塞缸套组件质量或装配质量不合格；经常猛轰油门，柴油机高速大负荷运行及温度过高［1-3］。

图7为与内模控制结构图对应的等效反馈控制结构图。

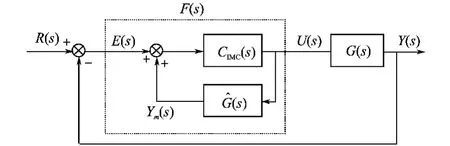
图7 等效反馈控制结构图Fig.7 The block diagram of equal feedback control

4.2 三相电压型PWM整流器的内模解耦控制

4.2.1 电流内模解耦控制

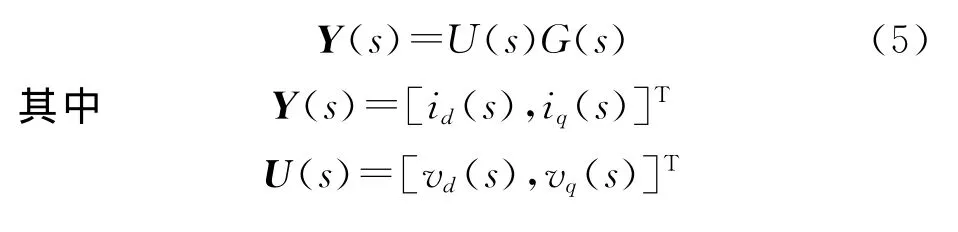
为提高系统鲁棒性，引入低通滤波器

则所设计的IMC控制器的CIMC（s）为

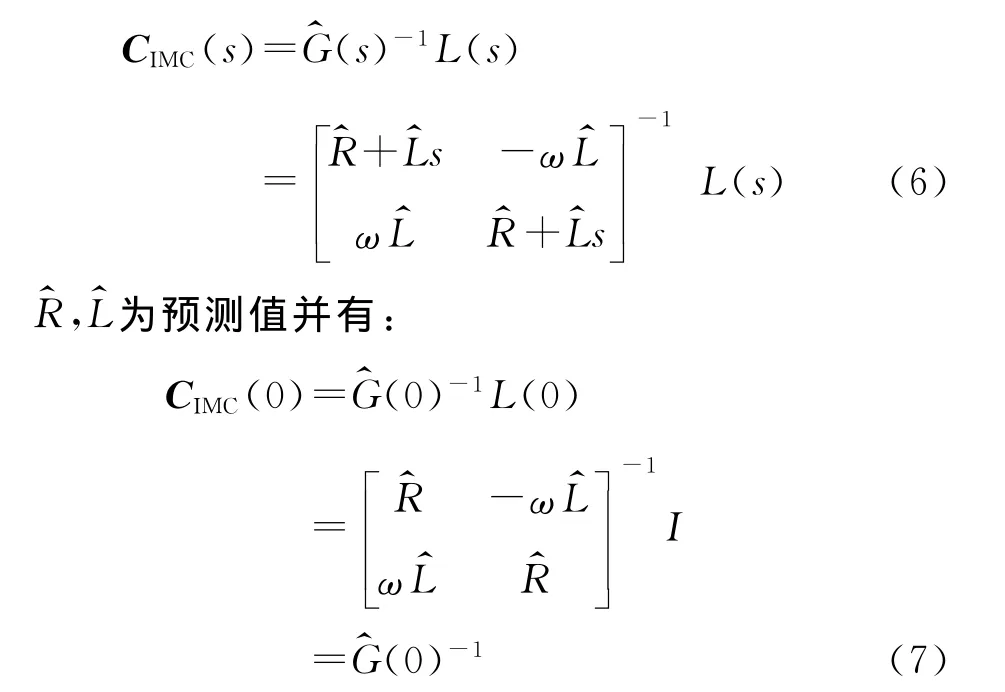
将内模控制结构按图7（除虚线部分）等效处理，则等效反馈控制器F（s）为

在式（9）中，主对角线上元素为电流控制器传递函数表达式，反对角线上元素则为内模解耦网络的传递函数。图8示出内模解耦实现控制框图。

图8 PWM整流器内模解耦结构图Fig.8 The block diagram of IMC decoupling for PWM

4.2.2 内模解耦控制作用

采用电流内模解耦控制，可有效抑制干扰及模型失配对输出的影响，并增强系统对给定信号的跟踪能力。

1）当PWM整流器的实际参数与内模匹配，即G（s）＝（s）时，忽略干扰D（s），可得：

可见，电流有功分量和无功分量无耦合，即实现了完全解耦。如果令λLd＝Kd，λLq＝Kq，Tid＝Ld／R，Tiq＝Lq／R，式（10）可变化为

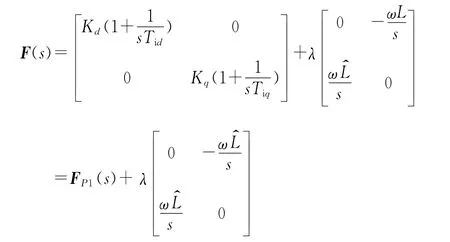
从上式可以看出，内模控制是PI控制器的基础上加一反角阵用以解耦。因此，内模控制是PI控制的一种特殊情况。

2）当PWM整流器的实际参数与内模不匹配，即G（s）≠（s）时，由于：

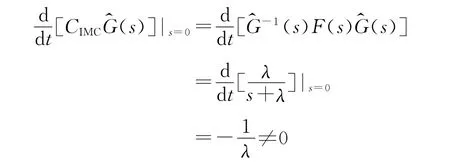
可见，基于内模控制的PWM整流器，当模型数和实际模型失配时，对阶跃输入和常值干扰不存在稳态偏差。

5 对三相电压型PWM整流器解耦控制的仿真分析

在反馈解耦控制中，解耦式中用实际d轴电流id和q轴电流iq来计算去耦电压，当且仅当PWM整流器参数估计准确时，耦合电压才能消除，否则存在耦合，且耦合程度取决于参数估计误差。而内模解耦控制原理分析表明：PWM整流器的参数的变化对定子电流的解耦效果影响不大。为了进一步验证上述结论，下面对其进行计算机仿真分析比较。仿真所用的PWM整流器参数为：电阻R（s）＝0.435Ω，L＝71.3mH，ωL＝7.423。

1）PWM整流器参数Lω＝时，反馈解耦仿真结果分析见图9。

图9 参数一致时的反馈解耦效果输出波形Fig.9 While parameters are consistenting，the output curves based on feedback decoupling

由图9可见，d轴给定信号i＊d在t＝2s从出现阶跃变化时，q轴输出实际值iq不受影响；同样在t＝4s，i＊q出现阶跃变化时，d轴实际值id也不受影响。这表明q轴分量iq和d轴分量id是相互独立的，PWM整流器的电压得到了解耦。所以，当PWM整流器参数Lω＝时，反馈解耦控制有较好的解耦效果。

2）当PWM整流器参数Lω≠时，反馈解耦仿真结果分析见图10。

图10 参数不一致时反馈控制解耦输出波形Fig.10 While parameters are not consistenting，the output curves based on feedback decoupling

由图10可知，当PWM整流器参数Lω≠时，反馈解耦控制的解耦效果不佳，d轴分量和q轴分量之间仍存在较大的耦合。

3）当PWM整流器参数Lω＝时，内模解耦仿真结果分析见图11。

图11 Lω＝ω时的内模控制解耦输出波形Fig.11 While Lω＝ω，the output curves based on IMC decoupling

当PWM整流器参数Lω＝，参数λ＝100时，内模解耦控制的解耦效果较好，PWM整流器得到了很好的解耦，输出的信号能较好地复现输入。

4）PWM整流器参数Lω≠时，内模解耦仿真结果分析见图12。

图12 Lω≠ω时的内模控制解耦输出波形Fig.12 While Lω≠ω，the output curves based on IMC decoupling

PWM整流器参数Lω≠，参数λ＝100时，内模控制仍能很好的解耦，输出信号能较好复现输入。

6 结论

本文首先介绍了多变量系统的各种特点以及其耦合特性，并在其基础上对PWM整流器进行了解耦分析。基于感应电动机定子电流解耦控制思想，对三相电压型PWM整流器电流内模解耦控制策略进行了研究，给出了内模解耦控制器的设计及实现方案，并进行了仿真实验。通过把内模解耦控制与反馈解耦控制的仿真结果进行了对比，可以看出：在参数一致时，两种控制方法都能对系统进行有效解耦，但内模控制比反馈解耦控制复现效果更好。当参数不一致时，反馈解耦控制失去了解耦的性能，但内模控制仍然可对系统进行解耦。

［1］ 全吉男，王聪，韩春艳.三相电压型PWM整流器的内模解耦控制［J］.电力电子技术，2007，41（7）：14-16.

［2］ 张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2005.

［3］ 周渊深.感应电动机交叉耦合电压的内模解耦研究［J］.机床与液压，2008，36（7）：357-360.

［4］ 柴天佑.智能解耦控制技术及应用［J］.设备管理与维修，2005，1（2）：53.

［5］ 徐丽娜.神经网络控制［M］.哈尔滨：哈尔滨工业大学出版社，1999.

［6］ 蔡自兴.智能控制—— 基础与应用［M］.北京：国防工业出版社，1998.

修改稿日期：2010-11-16

Research of Decoupling and Control on Three-phase PWM Voltage Rectifier

QIN Jing，LI Shi-guang，JIANG Zheng-you

（SchoolofInformationandElectricEngineering，ChinaUniversityof MiningandTechnology，Xuzhou221008，Jiangsu，China）

The topology structure of three-phase PWM voltage rectifier was introduced firstly and then analyzed the decoupling of the PWM rectifier.The simplified and controllable model of three-phase voltage source PWM rectifier can be realized by static and rotary coordinate transformation.The vector control based on rotary transformation could fail to decouple without accurate model and incomplete accordance between model parameters and system parameters which affects the system control performance.In order to achieve reliable and safe decoupling control，based on stator current decoupling control theory of induction motor，current internal model decoupling control strategy of three-phase voltage source PWM rectifier was proposed.The design and the scheme of the controller are given and all conclusions are supported by simulation.The results are favorable.

multivariable systems；decoupling control；internal-model decouplingcontrol

TM464；TN787

A

秦静（1986-），女，硕士，Email：cwhsh2009＠163.com

2010-04-27