转子振动故障的过程功率谱熵特征分析与定量诊断

费成巍,柏树生,白广忱,艾延廷

（1.北京航空航天大学能源与动力工程学院，北京 100191;2.沈阳航空航天大学动力与能源工程学院，沈阳 110136）

1 引言

信息熵是对系统不确定程度的描述，是定量指标，可用于转子振动状态变化情况的定量分析。近几年,信息熵方法作为信息处理手段在国内外得到了长足发展，在机械故障诊断中的应用研究相当活跃。但是，大多数研究均为基于状态的故障诊断方法，缺少对振动过程规律的描述。

华中科技大学的陈非等提出了基于过程的定量诊断方法[1]，通过多测点多转速下的信息熵矩阵很好地描述了振动过程的变化规律。然而，在信息熵中引入信息融合的思想对转子振动过程故障定量诊断还没有引起重视。

本文基于数据层信息融合思想，在转子试验台上模拟了4种典型故障特征信号，以信息熵方法为基础，提取了过程功率谱熵故障特征，并利用融合过程功率谱熵差矩阵对转子振动的故障类型以及故障严重程度进行了定量诊断分析。

2 功率谱熵的过程定量诊断方法

2.1 振动信号的信息熵特征

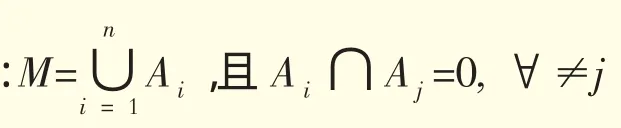
式中：μ (Ai)为集合 Ai的测度，i=1,2,…，n。

对于转子振动频域信号，需要进行信息熵特征提取，进而求出功率谱熵。

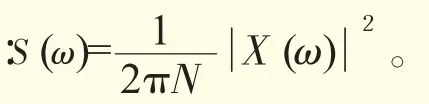
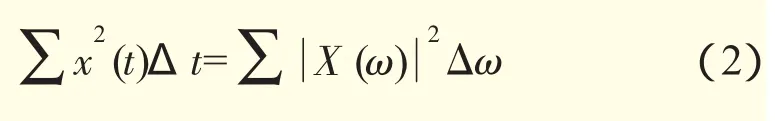
因此，S＝ {S1，S2，…，SN}可以看作是对原始信号的1种划分。由此可以定义相应的信息熵，即功率谱熵（记作Hf，下标f表示频域）

式中：qi第i个功率谱在整个谱中所占百分比。

功率谱熵表征了单个通道振动信号的谱型结构情况。振动能量在整个频率成分上分布得越均匀，则信号越复杂，不确定性程度也就越大。对于转子振动故障诊断来说，由于缺少定量指标，只利用信息熵来对转子故障进行诊断效果不太理想。在转子振动典型故障状态下，可以根据表征转子各系统状态的信息熵大小及其工作状态来判断是否有故障。然而，对于任意1种故障，由于采集振动波形的时刻和测点不同，计算得到的功率谱熵值有一定的分布区间。表1列举了4种典型故障的重叠功率谱熵区域，如果1个未知故障类型的功率谱熵值为1.0，就很难判断此类故障属于这4种故障中的哪1种。

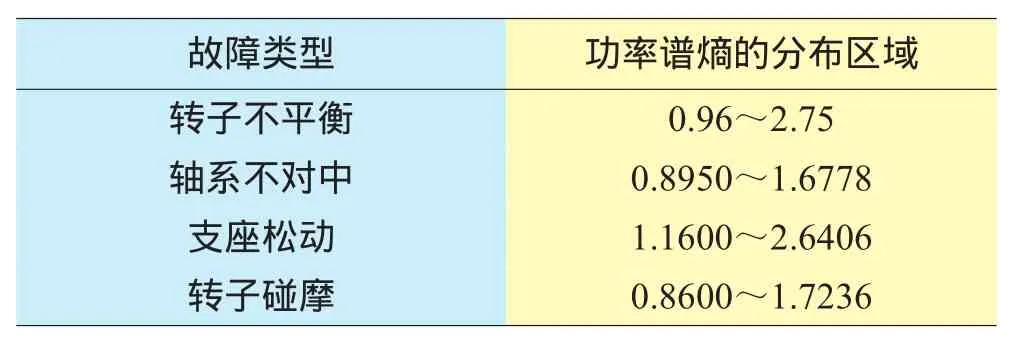
表1 转子振动故障的功率谱熵分布区间

2.2 基于过程功率谱熵的定量诊断方法

功率谱熵差矩阵方法在一定程度上能解决上述难题。假设功率谱熵矩阵A(M×N)是转子振动任意1种典型故障的诊断样本，其中M表示升速或降速过程中振动信号采样点的个数，N表示振动信号的测点个数。矩阵A中的任意1个元素Aij就表示在第i个采样转速下第j个通道的功率谱熵值。对于未知故障类型的振动信号(即目标振动信号)进行同样的升速或降速数据采集，就可以得到M×N的功率谱熵矩阵B。为了比较功率谱熵矩阵B和A的过程规律，首先将2个矩阵相减求得功率谱熵差矩阵H

分别求功率谱熵差矩阵H的均值和方差矩阵

同理，可以求出目标振动信号与转子典型振动故障之间的功率谱熵差矩阵的均值和方差。通过求取其中均值绝对值和方差的最小值，就可进行故障判别。功率谱熵差矩阵的均值绝对值越小，表示目标振动信号的功率谱熵值分布区间与故障样本振动信号的功率谱熵值分布区间越接近，即目标振动信号属于这种故障的可能性越大；反之亦然。若目标振动信号的功率谱熵值分布区间与各故障样本振动信号的功率谱熵值分布区间都很接近，则需通过信功率谱差矩阵的方差值比较。功率谱熵差矩阵的方差反映了2种故障的相似程度，方差越小，表示目标振动信号的功率谱熵值的过程分布规律与振动故障样本功率谱熵值的过程分布规律越接近，即目标振动信号属于该故障的可能性越大；反之亦然。

3 转子振动故障模拟试验

转子升速过程是由很多状态构成的过程，在不同的转速下，振动形态不同，按照转速间隔或时间间隔采集的振动波形记录了丰富的信息。1种故障在某一时刻或某一状态下引起的振动表现具有一定的分散性和随机性，但在一个过程中却有其规律性。多测点多转速下的信息熵值组成的信息熵矩阵是多种状态的综合，这个信息熵矩阵反映了振动信号的过程规律。因此，可以通过信息熵矩阵来描述转子振动信号的过程规律。

转子试验台和试验测量系统如图1所示。为了研究转子振动的过程特征，在转子试验台上进行了4种典型故障（转子不平衡、轴系不对中、支座松动和转子碰摩）的模拟试验；每种故障都设计在1000～3000 r/min转速范围内来模拟，每种情况都分别进行多次升降速试验，振动信号采样的转速间隔设为100 r/min；试验系统布置了4个振动测点（测加速度），即4点振动信号，因此每次升降速试验能采集到每种故障模式的84组振动信号(1组振动信号对应某一振动测点的1个采样转速下的振动波形)来反映升速或降速的过程特征，进而对每种故障都可得到多个能反映其过程特征的原始数据集合。

每组振动波形信号都可求出上述的功率谱熵值,对任意1种故障，将最能反映其过程特征试验的多测点多转速下的功率谱熵值都计算出来，就得到1个以功率谱熵矩阵作为该种故障的诊断样本。

4 计算实例

4.1 转子振动故障功率谱熵矩阵计算

通过Matlab编程对采样得到的各种故障模式的振动信号进行计算，得到各种故障类型的功率谱熵矩阵。各种故障的功率谱熵值的分布区间见表1。对于任意1种故障，由于采集振动波形信号的时刻和测点不同，计算得到的功率谱熵值会在一定的数值范围内波动，有一定的分布区间，因此，仅仅依靠功率谱值来进行故障诊断是行不通的。

4.2 目标信号选取和故障功率谱熵差矩阵计算

为了便于计算，选取1个基准信号的功率谱熵矩阵作为目标振动信号。图2是在相同试验条件下,模拟的另1次支座松动故障的3维图。

把目标振动信号（图2）的功率谱熵矩阵分别与每种故障的功率谱熵矩阵样本相减,就得到4个功率谱熵差矩阵，其3维图如图3～6所示。

分别求得4个功率谱差矩阵的均值绝对值和方差。其结果见表2。

表2 功率谱熵差矩阵的均值绝对值和方差

由表2中可见：从相对应的4种故障功率谱熵差矩阵的均值绝对值来看，虽然可以诊断出目标信号的故障模式为支座松动，但由于均值的绝对值的区别不太明显，所以诊断效果不太准确。从其方差来看，目标故障振动信号与支座松动故障功率谱熵差矩阵的方差值最小，并与其他最小值相差10倍以上，即目标故障振动信号的信息值过程分布规律与支座松动故障的功率谱熵值的过程分布规律较好吻合，故可以诊断为支座松动故障，与事实相符。

4.3 故障严重程度的诊断

为了用功率谱熵矩阵来诊断某种故障的严重程度，选取支座松动故障进行诊断，以转子正常工作状态（无故障模式）的振动信号为基准振动信号,功率谱熵矩阵用A表示。分别以1个和2个支座松动来模拟2种支座松动故障模式，用其振动信号功率谱熵矩阵作为目标功率谱熵矩阵，分别用B1和B2表示相应2种故障矩阵。分别求H1=B1-A和H2=B2-A，及其均值绝对值和方差。均值绝对值和方差的大小决定了故障严重程度，均值绝对值和方差越大，故障越严重；反之亦然。诊断结果见表3。

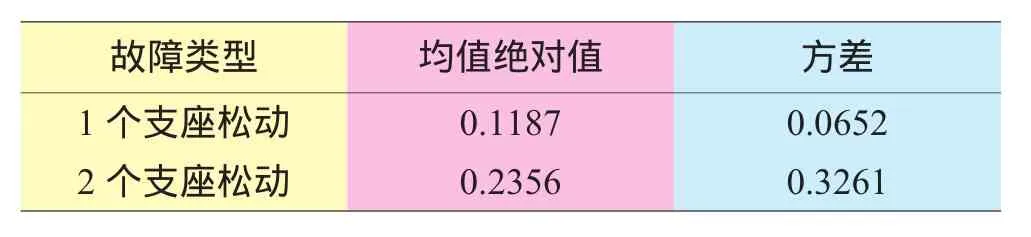
表3 故障严重程度诊断结果

从表3中可见，1个支座松动的故障模式的功率谱熵差矩阵的均值绝对值和方差明显比2个支座松动故障模式的功率谱熵差矩阵的小，说明1个支座松动故障模式的故障严重程度较小，与假设相符。因此，利用功率谱熵差矩阵能对故障严重程度有效判别。

5 结论

基于过程诊断方法，提出了转子故障定量诊断方法。通过转子试验获取振动故障数据，得到转子振动过程信号变化规律的指标-功率谱熵矩阵，然后通过计算功率谱熵差矩阵的均值绝对值和方差，能够定量地比较2次振动过程变化吻合程度，从而得到比较准确的基于过程规律的判别结果。

通过分析转子振动信号的实例得出，基于过程融合功率谱熵的转子振动故障诊断方法能够很好地区分故障类别和判断故障的严重程度。但由于大型复杂的旋转机械振动故障本身的复杂性，因而该方法能否有效区分故障的发生部位，还需做进一步研究。

[1]陈非,黄树红,张燕平,等.基于过程的旋转机械振动故障定量诊断方法[J].动力工程,2008,28（4）:543-547.

[2]费成巍,艾延廷.航空发动机健康管理系统设计技术[J].航空发动机,2009,35（5）:24-29.

[3]Xing Xiu-san.Physical Entropy,Information Entropy and Their Evolution Equations[J].Science in China Series A,2001,44(10).1331-1339.

[4]Endo H,Randan R B.Enhancement of Autoregressive Model Based Gear Tooth Fault Detection Technique by the Use of Minimum Entropy Deconvolution Filter[J].Mechanical Systems and Signal Process,2007,21（2）:906-919.

[5]Yang W X,Hull J B,Seymour M D.Detecting the Singularities in Engineering Signals [J].JournaI of Materials Processing Technology,2006,175（1-3）:439-445.

[6]Li Hong-kun,Zhou Pei-lin,Ma Xiao-jiang.Pattern Recognition on Diesel Engine Working Condition by Using a Novel Methodology-Hubert Spectrum Entropy[J].Proc.Inst.Mar.Eng.Sct.Technol.Part AJ.Mar.Eng.Technol,2005（6）:43-48.

[7]Qu Liang-sheng,Li Liang-ming,Lee Jay.Enhanced Diagnostic Certainty Using Information Entropy Theory [J].Advanced Engineering Informatics,2003,17（3-4）:141-150.

[8]李金涛,张凤鸣,李永宾,等.基于多元联合熵的航空发动机性能分析[J].控制系统,2007,23（1）:53-54.