混凝土徐变应力计算方法及应用

陈 江，段会文

（中国水电顾问集团昆明勘测设计研究院科学研究分院，云南 昆明 650033）

应力应变监测是混凝土坝的重要监测内容。坝体内部混凝土的应力应变监测主要采用应变计（组），常用的应变计 （组）有九向、七向、五向、四向等。应变计 （组）只能监测应变计埋设方向的应变，该应变包含了温度应变、混凝土自生体积应变、徐变应变及应力应变等，而工程上更关心的是混凝土的应力。因此，需要结合混凝土徐变试验成果将应变转换为应力。混凝土徐变应力常用的计算方法有：应力增量法[1,2]、松弛系数法[3]和隐式解法[2]等。本文对应力增量法进行改进，增加主应力计算，并基于MATLAB编写计算及绘图程序，将本程序应用于金安桥水电站碾压混凝土重力坝，分析坝体内部混凝土的应力状态。

1 徐变应力计算方法

将应变计 （组）应变测值转换为徐变应力值的技术路线为：①应变计 （组）测值的补偿；②应变计 （组）测值的调整[1,4,5]；③各方位应变计徐变应力的计算[1,6]；④空间应力的计算；⑤主应力的计算。完成技术路线的①～③后可得到应变计 （组）埋设方位的应力值。九向应变计 （组）的埋设方位见图1。

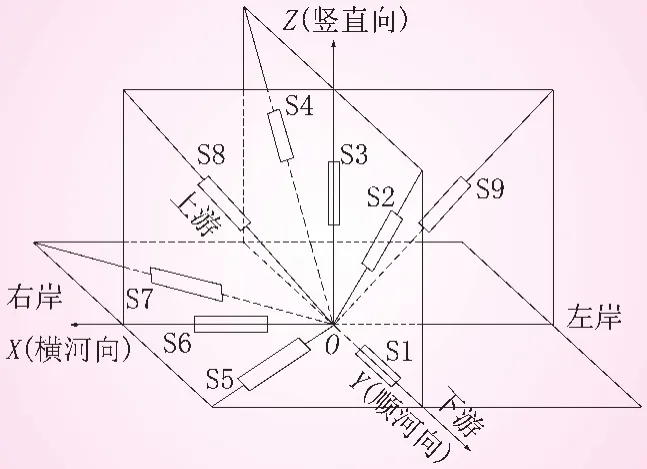
图1 九向应变计 （组）示意

根据图1可得空间应力分量为

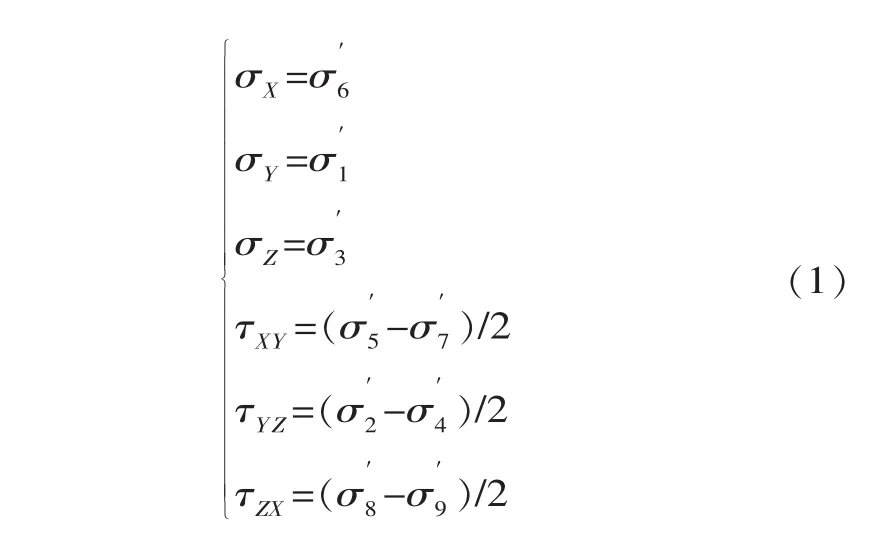
式中， σX、 σY、 σZ、 τXY、 τYZ、 τZX为空间应力分量， MPa；为第i个应变计所测方位的徐变应力，MPa。

根据弹性力学应力状态特征方程，主应力满足

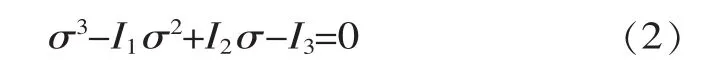
式中，I1、I2、I3分别为应力第一、第二、第三不变量。

由式（2）可得 3 个实根， 分别为 σ1、 σ2、 σ3， 并且 σ1≥σ2≥σ3。 由此， 可得最大剪应力

2 徐变应力计算程序开发

根据徐变应力计算方法，采用MATLAB编写徐变应力计算及绘图程序。程序流程：

（1）输入计算参数，包括：通过混凝土弹性模量试验、徐变试验得到的瞬时弹性模量方程和徐变方程的拟合参数、混凝土浇注时间，可将各分区徐变试验参数写成元包数组保存成MATLAB数据文件，形成徐变试验参数数据库，待计算时调用。

（2）根据应变计 （组）各应变计测值及对应无应力计测值，进行应变计 （组）测值的补偿，可通过MATLAB中的插值函数interp1对测值进行加密或平滑处理。

（3）若应变计 （组）测值不满足弹性力学平衡条件，则对各方位应变计测值进行平差处理，即应变计 （组）测值的调整。

（4）根据应力增量法的递推公式

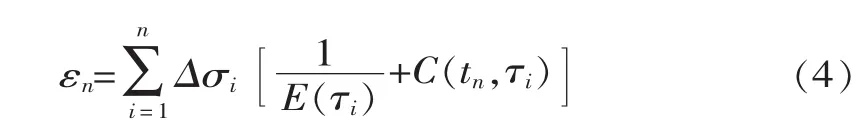
计算每个监测期应变计 （组）各方位的徐变应力值。式（4）中， εn为 tn时刻的总应变， 10-6； △σi为 τi时刻的应力增量， MPa； E（τi）为 τi时刻的瞬时弹性模量， MPa； C（tn，τi）为混凝土龄期为 τi、 在 tn时刻的徐变度，MPa-1。

（5）进行空间应力分量和主应力的计算，其中主应力计算需要解一元三次方程，可直接利用MATLAB中的roots函数实现。

（6）计算成果输出，包括徐变应力时程曲线的绘制和徐变应力特征值的提取。可通过MATLAB中的plotyy函数实现双坐标轴曲线的绘制，在绘制曲线时需将日期改成数值格式，绘制完曲线，标注刻度时，可采用datevec、datestr、datenum等命令将数值格式表述的日期转换为日期格式。徐变应力特征值可通过max、min、sum、length等函数找到。特征值对应的监测日期可采用find函数找到应力极值对应的应力矩阵 （数组）的行数，日期数组中与该行数对应的日期即为特征值对应的监测日期。

3 工程应用

金安桥水电站工程位于云南省丽江市境内的金沙江中游河段上，是金沙江中游河段规划的第5级水电站。总装机容量2 400 MW，挡水建筑物为碾压混凝土重力坝，坝顶高程1 424 m，最大坝高160 m，坝顶长640 m。坝体内部混凝土的应力应变监测主要采用五向应变计 （组）。结合各分区混凝土徐变试验成果，采用徐变应力计算程序将金安桥水电站应变计 （组）的应变监测成果转换为徐变应力成果。作为代表性示例，本文仅给出14号坝段部分五向应变计 （组）测点的徐变应力计算成果 （见图2），A14-S5-01、A14-S5-03和A14-S5-08这三个测点均位于0+403.500纵剖面，靠近上游坝面，三个测点所处高程不同。徐变应力特征值统计见表1。

从图2上看，这三个测点的正应力基本为负，处于受压状态，局部某些时刻可能由于测值误差等因素而出现较大拉应力，其徐变应力计算成果基本符合坝体现阶段的受力特征。A14-S5-01测点位于最底层，最大压应力为-6.45 MPa；A14-S5-03测点靠近A14-S5-01测点，二者徐变应力计算值较为接近，A14-S5-03测点最大压应力为-4.09 MPa；A14-S5-08测点靠近坝体中部，压应力明显小于其他两个测点，最大压应力为-3.00 MPa。各测点的徐变应力变化趋势较为平缓，局部时段稍有波动。

经分析，徐变应力计算值可能受多个因素影响而产生较大误差，主要因素有：

（1）监测时间间隔较长，尤其是监测前期，导致该时段的徐变应变无法准确计入。

（2）应变计测值不全或损坏，无法进行全程的应变不平衡量调整。

（3）应变不平衡量较大，与弹性力学理论相违背，可能是个别应变计测值有误所致。

（4）与应变计 （组）对应的无应力计测值有误，导致进行体积应变补偿时应变值失真。

（5）混凝土弹性模量试验和徐变试验所用试件的代表性 （混凝土试件是否与测点处混凝土相符）。

图2 徐变应力时程曲线

（6）计算误差的传递性 （某一时刻的计算误差会给此时刻以后的计算值带来误差）与累积性。

4 结论

（1）基于MATLAB编写了采用应力增量法进行徐变应力计算及绘图的程序。该程序利用MATLAB强大的数值计算及绘图功能，可方便快捷地得到测点各监测时刻的应力状态及时程曲线。

（2）徐变应力计算程序应用于金安桥水电站碾压混凝土重力坝，计算分析坝体内部混凝土的应力状态。给出了14号坝段的部分徐变应力计算成果，结果表明：计算所得应力状态与坝体现阶段的受力特征基本相符。实践效果表明该程序快捷、有效，值得推广。

（3）徐变应力计算受众多因素影响，其误差源较多，为了得到较为准确的徐变应力计算成果，需要在监测实施阶段 （监测施工、数据采集等）、混凝土徐变试验以及计算中多加注意。

表1 徐变应力特征值统计 MPa

［1］ 管志成.混凝土坝应变计测值的应力计算［J］.水利学报，1980（3）： 72-76.

［2］ 朱伯芳.混凝土结构徐变应力分析的隐式解法［J］.水利学报，1983（5）： 40-46.

［3］ 门远，林坚，张日勇，等.五向应变计的松弛法应力计算［J］.水利水电技术， 2004， 35（3）： 27-28.

［4］ 郭晨.大坝内部 “七向”应变计组平差公式的改进探讨［J］.大坝观测与土工测试，1992（4）：45-46.

［5］ 朱赵辉，包腾飞，汪亚超，等.应变计组的因果关系模型有效性判断算法研究［J］.重庆建筑大学学报， 2008， 30（5）： 100-104.

［6］ 朱伯芳.混凝土的弹性模量、徐变度与应力松弛系数［J］.水利学报， 1985（9）： 54-61.