反应率线性外推含钆燃料燃耗计算方法的改进

陈国华,俞陆林,蒋校丰,张少泓

(上海交通大学核科学与工程学院,上海 200240)

PC方法[1]是传统的核燃料组件燃耗计算方法,实际应用表明,该方法对不含钆组件是适用的,但对含钆组件,由于155Gd及157Gd的吸收截面巨大,钆毒物棒内热中子注量率的空间分布随燃耗变化显著,因此,为准确预测钆毒物棒的燃耗,除需在棒径上细分燃耗区外,还必须采用很小的燃耗步长。虽然PC方法燃耗计算本身代价不高,但由于为获得各燃耗区的反应率必须进行代价高昂的组件输运计算,因此,从实用角度,有必要对燃耗计算方法进行改进,尤其是在当前含钆毒物的应用越来越普遍的情况下,这样的改进更为必要。

本文从钆同位素的微观反应率随核子密度的变化关系出发,在 PPC方法[2]基础上,针对155Gd和157Gd提出了反应率对数线性外推方法,并以含钆压水堆组件为对象,对该方法进行了检验。

1 理论模型

在传统PC方法中,首先用燃耗步初的微观反应率RP和核子密度Nn求解燃耗方程,得到燃耗步末tn+1时刻核子密度的预测值+1,然后用此核子密度进行输运计算得到新的微观反应率RC,用RC和初始核子密度Nn再解一遍燃耗方程得到tn+1时刻核密度的修正值,最终取预测值和修正值的平均作为燃耗步末tn+1时刻的值：

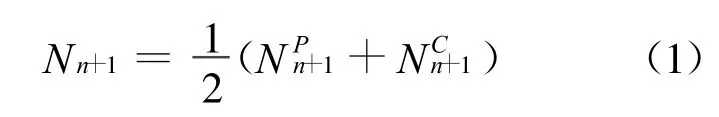
上述方法中修正步的反应率RC是基于预测步的核子密度N获得的,由于预测步计算本身存在误差,所以反应率RC也不准确,尤其是当组件含钆时,钆毒物棒内的中子注量率随燃耗迅速增加,相应的反应率也显著增大,但由于预测步计算是在假设反应率保持为燃耗步初始时刻的低水平下进行的,这就导致钆的燃耗速率偏低,修正步反应率RC偏小,并最终导致由式(1)算得的钆的核子密度偏大。

为改善上述问题,文献[2]基于PC方法提出了PPC方法。该方法利用PC方法的中间结果来构造微观反应率随核密度线性变化的关系,即：

可以预计采用式(2)将弥补PC方法常数反应率假设的不足。但由于直接利用式(2)将导致燃耗方程非线性,为此PPC方法先利用式(1)所得的核子密度Nn+1由式(2)计算出改进的修正步反应率˜RC：

然后再用此反应率˜RC进行燃耗计算得到新的修正步核子密度˜,并最终令燃耗步末的核子密度为：

可以看出,和PC方法相比,PPC方法在每个燃耗步内都要多一次燃耗计算,但由于PPC方法可在比 PC方法大得多的燃耗步长条件下,获得更准确的结果[2],因此其整体计算效率要优于PC方法,再加上PPC方法只需在PC方法基础上稍作改动即可实现,因此PPC方法在国际上已被大家认为是含钆组件燃耗计算的一种好方法。

近来,文献[3]的研究表明,对于155Gd、157Gd等强吸收核,其微观反应率与核密度的对数值(lnN(t))之间具有更好的线性关系。为此对于155Gd、157Gd等强吸收核本文采用式(5)取代式(3)进行反应率的外推：

其余核的处理则仍按PPC方法进行。

需指出的是,当出现预测步的核子密度很接近于Nn的情况时,无论采用式(3)或式(5),反应率外推的结果都将不可靠,故不应作外推。但考虑到此时微观反应率的误差也相当小,所以当出现这样的情况时,传统PC方法的精度已经能够满足要求。

2 数值验证

为检验不同燃耗计算方法性能的差异,本文以文献[4]所给出的压水堆组件为对象,分别采用传统PC方法、文献[2]的PPC方法(以下用PPC-1表示)以及本文方法(以下用PPC-2表示)进行了计算。图1给出了所计算组件的1/4对称布置,其中,UO2燃料棒中235U的富集度为6.5 w/o,而含钆燃料棒中235U的富集度为4.0 w/o,Gd2O3的质量分数为10.0 w/o。所有材料的温度都设为300 K,水的密度为1.0 g/cm3,组件平均功率密度为37.5W/g,燃耗700 d。

本文首先用PC方法,以1天为1个燃耗步(ΔBu=37.5MW◦d/tU)进行计算,并将所得结果作为随后比较的参考解。参考解组件k∞随燃耗的变化如图2所示。图3给出了组件内钆燃耗速率最快的燃料棒(其对称位置之一用数字标注于图1中)其157Gd的参考燃耗特性。

为检验大燃耗步长情况下不同方法的计算精度,接下来分别以15 d、25 d和35 d为步长,分别用PC、PPC-1和PPC-2方法进行了计算,所得结果与参考解的误差如图4～图6所示。不同方法所得的59号钆棒内157G d总核子密度的误差如图7～图9所示。需说明的是,为考虑燃耗初期快饱和裂变产物的积累,在所有燃耗计算中,前两步步长均取2 d和8 d。

图1 17×17含钆PWR 1/4组件布置图Fig.1 Quadrant layout of the Gad-loaded PWR assemb ly

从上述比较可以看出,一方面,传统PC方法在大燃耗步长下进行含钆组件的燃耗计算会导致十分显著的误差,而和PC方法相比,基于反应率外推的PPC-1和PPC-2方法其精度都有明显改进。另一方面,从PPC-1和PPC-2方法的相互比较可看出,当燃耗步长相对较小时(如采用15 d为步长),两者的精度都令人满意,其中文献[2]的PPC方法还略优于本文提出的改进方法,但随着燃耗步长的进一步增大,如采用25 d(0.937 5GW◦d/t)或35 d(1.312 5 GW◦d/t)为步长时,本文所提出的改进方法精度更优。

图2 k∞随燃耗变化Fig.2 k∞as function of burnup

图3 59号燃耗棒中157 Gd的燃耗Fig.3 157Gd dep letion in fuel pin 59

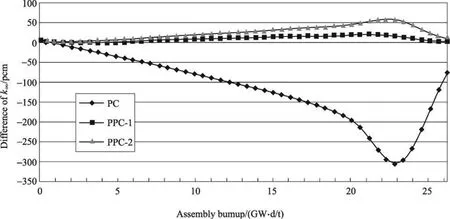
图4 15 d/燃耗步(0.562 5 GW◦d/t)下 k∞误差随燃耗变化Fig.4 k∞difference using 15-day(0.562 5 GW◦d/t)timestep intervals

图5 25 d/燃耗步(0.937 5 GW◦d/t)下 k∞误差随燃耗变化Fig.5 k∞difference using 25-day(0.937 5 GW◦d/t)timestep intervals

图6 35 d/燃耗步(1.312 5 GW◦d/t)下 k∞误差随燃耗变化Fig.6 k∞difference using 35-day(1.312 5GW◦d/t)timestep intervals

图7 15 d/燃耗步(0.562 5GW◦d/t)时59号燃料棒中157Gd核子密度绝对误差随燃耗变化Fig.7 157 Gd concentrations abso lute difference in pin 59 using 15-day(0.562 5 GW◦d/t)timestep intervals

图8 25 d/燃耗步(0.937 5 GW◦d/t)时59号燃料棒中157Gd核子密度绝对误差随燃耗变化Fig.8 157 Gd concentrations absolute difference in pin 59 using 25-day(0.937 5 GW◦d/t)timestep intervals

图9 35 d/燃耗步(1.312 5 GW◦d/t)时59号燃料棒中157Gd核子密度绝对误差随燃耗变化Fig.9 157Gd concentrations absolute difference in pin 59 using 35-day(1.312 5 GW◦d/t)timestep intervals

3 结论

本文在文献[2]提出的PPC方法的基础上,从钆同位素的微观反应率随核子密度的变化关系出发,提出了对强吸收核按其核密度的对数来外推反应率的方法。针对含钆压水堆组件的数值验证表明,本文方法可以在更大的燃耗步长条件下,获得比PPC方法更高的精度。

致谢

感谢赵荣安教授在本文研究工作过程所给予的多次有益的讨论和指导。

[1] 谢仲生.压水堆核电厂堆芯燃料管理计算及优化[M].北京：原子能出版社,2001,111-112.

[2] Akio Yamamoto.Projected Predictor-Corrector Method for Lattice Phy sics Bu rnup Calcu lations[J].Nuclear Scien ce and Engineering,2009,163：144-151.

[3] Akio Yamamoto,Tadashi Ikehara,Takuya Ito.Benchmark Problem Suite for Reactor Physics Study of LWR Next Generation Fuels[J].Jou rnal of Nuclear Science and Technology,2002,39：900-912.