基于矢量修正的幅值算法在电源切换装置中的应用

曹 祯 秦雷鸣 赵吉生 顾新波

（西门子电力自动化有限公司，南京 211100）

1 引言

在电力系统中，对于供电可靠性要求较高的重要用户或变电站，必须具备两个或多个供电电源，但是为了减小短路容量、合理分布潮流和避免电磁环网，一般采取由一个供电电源作为工作电源，其余电源作为备用的运行方式。同时加装电源切换装置，在工作电源因某种原因故障跳闸或者检修时，由电源切换装置主动而快速地切换到备用电源上，使用户或变电站重新获得电源。

目前国内电源切换装置主要分为两大类：电源快速切换装置（简称快切）和备用电源自动投入装置（简称备自投）。快切装置的切换速度很快从而尽可能降低切换到备用电源时的电流冲击和扭矩冲击，在尽可能缩短负载断电时间的情况下保证电动机的安全。备自投装置的切换速度较慢，它的关键是切换逻辑的正确性。

目前国内电源切换装置主要用于以下两种工况：

（1）工况（a）（见图 1）给出了单母两进线接线方式，通常情况下，母线将被进线 1或者进线 2供电，如果CB1在合位且CB2在跳位，则进线1为工作电源，进线2为备用电源。如果进线1因为故障或者其他原因失电，则电源切换装置能够快速启动并且将母线切换到进线2。如果CB2在合位且CB1在跳位，则进线2为工作电源，进线1为备用电源。如果进线2因为故障或者其他原因失电，则电源切换装置能够快速启动并且将母线切换到进线1。

图1 单母两进线接线方式图

（2）工况（b）（见图2）给出了单母分段两进线接线方式，通常情况下，母线1将被进线1供电，母线2将被进线2供电， CB1和CB2在合位且CB3在跳位。如果其中一条进线因为故障或者其他原因失电，则电源切换装置能够快速启动并且将母线切换到另外一条进线。切换方向可以根据实际的 CB状态以及启动方式来自适应。

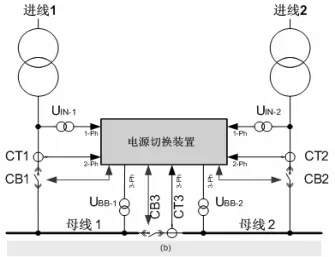
图2 单母分段两进线接线方式图

对于图 1中的工况（a）,每条进线的一个线电压和两相电流，以及母线的三相电压都要接入电源切换装置。对于图 2中的工况（b）,每条进线的一个线电压和两相电流，以及两条母线的三相电压和其中一条母线的三相电流都要接入电源切换装置。电源切换装置必须测量至少三个不同的频率（两条进线频率和母线频率）以及三个不同频率下的电压电流。电压电流的计算和压差，频差，相角差一样重要，因为这些幅值不仅要被用作切换判据，也被用于电源切换装置中的后备保护。

本文将介绍一种新的幅值算法，它可以大大提高母线频率突变时的幅值计算精度和响应速度。

2 国内电源切换装置用到的一种传统幅值算法

国内电源切换装置中用到的一种传统幅值算法是基于采样频率跟踪的全波傅里叶变换。

2.1 传统幅值算法实现方法

采样频率跟踪是一种根据实际测量频率来自动调整采样点间隔的机制，这个机制是全波傅里叶变换的基础。当装置测量到的频率有变化时（比如变化超过 0.02Hz），采样频率跟踪机制开始调整采样间隔。为防止扰动数据对采样点频率的影响，当装置测量到的频率有较大跳变时，采样频率跟踪机制一般不会立即将采样频率调整到实际测量频率，而是以某个固定变化率来调整采样频率（比如0.02Hz/ ms），直到采样频率被调整到与实际测量频率相等。

全波傅里叶变换是一种广泛应用于继电保护装置的算法，这个滤波器的输入是一个周波的采样点值，输出是基波值的实部和虚部。算法本身具有滤波作用，能抑制恒定直流和消除各种谐波，因而在工程实践中获得了广泛应用。

计算电压基波分量的全波傅里叶算法公式为

式中，Usin,Ucos 分别为基波的正弦分量和余弦分量；N为一个周波的采样点数，k，ku分别为第k次采样和采样值。

在得到基波的正弦分量和余弦分量之后，就可以得到幅值

当传统幅值算法被用于电源切换装置时，至少需要两套独立的采样频率跟踪机制，对应地就要使用两个中断源来实现进线和母线的采样频率跟踪。

2.2 传统幅值算法用于电源切换装置存在的问题

采用传统幅值算法计算母线和进线的电压电流会存在以下几点问题：

（1）传统幅值算法对频率突变的响应速度太慢，很大程度上会影响快切成功率。

传统幅值算法的基础是采样频率跟踪，所以传统幅值算法对频率突变的响应速度取决于采样频率跟踪对频率突变的响应速度。

将式（1）和式（2）的离散值进行z变换后的滤波函数可以表示为

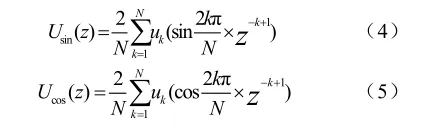
为了对式（4）和式（5）频率特性进行分析，现将其转换到复频域：

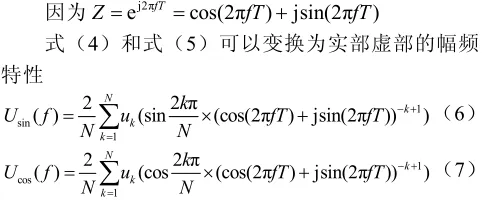
式（6）和式（7）中，f是实际电压电流的频率，T是采样点间隔。

由式（6）和式（7）不难看出，当采样频率和实际系统频率相等时，Z=1，全波傅里叶变换的结果是准确的，当采样频率和实际系统频率不相等时，Z≠1，且Z是和实际系统频率相关的衡量，此时全波傅里叶变换的结果有误差，采样频率和实际系统频率的偏差越大，全波傅里叶变换的结果误差也越大，这种情况下的计算结果是无效的。当额定频率为50Hz，采样点间隔固定为1ms时（即额定频率下每周波20点采样），全波傅里叶变换的幅频特性如图3所示。

图3 全波傅里叶变换的幅频特性

从图3可以看出：全波傅里叶变换实部和虚部的幅频特性不一致，其中实部幅频特性的边瓣较大，虚部幅频特性的边瓣较小。全波傅里叶变换实部幅频特性对56Hz的信号放大作用最强，达到1.03285，虚部幅频特性对 42Hz的信号放大作用最强，达到1.04303。

而采样频率跟踪需要一个过程，特别是对于系统频率突变较大的情况（大于1Hz），采样频率完成调整需要几十毫秒，再加上频率测量的数据窗长度，采样频率跟踪对于频率突变的整个响应时间一般在100ms以上。在这个时间段内，采样频率是不等于实际系统频率的，这就造成了全波傅里叶变换的结果在这个时间段内有比较大的误差。

如图1所示工况，工作电源被切除前，母线电压频率等于工作电源电压频率，当工作电源侧发生故障而被切除后，母线电压变成了电动机感应生成的电压，其频率对应于转子旋转速率，由于转子中励磁电流为衰减的直流，母线侧频率相对工作电源被切除前会有1～2.5Hz的突变，之后会一直衰减下去直到被切换到备用电源。因此在工作电源刚被切除后的几十毫秒甚至上百毫秒内，采样频率和实际母线频率是不相等的，这就造成了这个段时间内母线电压的计算结果有较大的误差，如果母线电压被用于快速切换判据，很可能造成快切的误动或拒动。

如图2所示工况，在工作电源刚被切除后的几十毫秒甚至上百毫秒内，母线电流的计算结果有较大误差，而母线电流用于保护母联断路器，很可能造成过流保护误动或拒动。

（2）采样频率跟踪中断会在一定程度上增加电源切换装置CPU负载率。

电源切换装置需要至少两个独立的采样频率跟踪机制，也就需要提供至少两个独立中断源来实现母线和进线的采样频率跟踪。当工作电源被切除后，母线侧频率相对工作电源被切除前会有1～2.5Hz的突变，之后会一直衰减下去直到被切换到备用电源，在此过程中，采样频率跟踪中断会在一定程度上抬高装置CPU负载率。

（3）采样频率跟踪会一定程度上增大频率和相角计算误差。

目前国内电源切换装置的测频大都采用过零点算法，而过零点算法的精度和过零点时标的计算有着直接关系。当采样点和过零点不重合时，需要用插值算法计算出过零点时标，如图3所示，tn1为一个过零点时标，a1，a2为这个过零点相邻的两个采样点值，t1，t2为这个过零点相邻的两个采样点时标，由插值算法可得

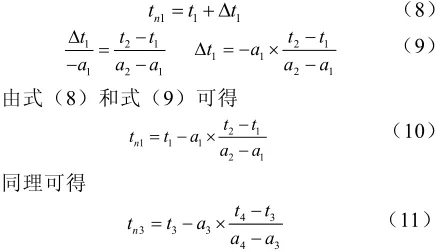
图4 过零点时标计算

由式（10）和式（11）可以看出，过零点时标的计算精度除了与采样点值的精度和时标相关，还和插值算法本身的误差有关。插值算法是一种近似处理，也就是说，在过零点附近，认为两个采样点和过零点是近似成一条直线的，很容易看出，采样点间隔越大，这种线性处理的误差也越大。现实应用中，当工作电源被切除后，母线侧频率相对工作电源被切除前会有1～2.5Hz的突变，之后会一直衰减下去直到被切换到备用电源，在此过程中，采样频率跟踪的存在会相应拉大采样点间隔，过零点时标的计算误差也相应变大，进而造成母线频率误差增大。

目前国内电源切换装置测角差大都采用过零点算法或者基于全波傅里叶变换得到的实部虚部。对于过零点算法，上面已经分析了采样频率跟踪对它的影响。对于全波傅里叶变换，上面已经分析了采样频率跟踪对全波傅里叶变换结果的影响。所以不论测角差选择哪种算法，采样频率跟踪都会对其产生不好的影响。

（4）传统幅值算法的数据窗长度会受采样频率跟踪的影响。

现实应用中，当工作电源被切除后，母线侧的频率可能会下降到比较低的值，采样频率跟踪的存在会相应地拉大采样点间隔，而全波傅里叶变换所需的采样点个数是一定的，这样就造成了传统幅值算法的数据窗长度被加长，而对于快速切换来说，数据窗长度直接影响到切换速度。

3 基于矢量修正的幅值算法

3.1 基于矢量修正的幅值算法简介

此算法不依赖于采样频率跟踪，采样频率跟踪机制可以被取消，采样点频率通常被固定为系统额定频率。算法数据窗为某个固定长度（比如20个采样点），固定数量的采样点经带通滤波器变换后得到初始实部虚部，同时根据实际测量频率和采样点频率的偏差求得相应的修正系数，对初始实部虚部进行修正得到精确的基波值实部虚部。

3.2 基于矢量修正的幅值算法实现

基于矢量修正的幅值算法可以在电源切换装置中得到很好地应用，下面举例说明其实现方法。假设电源切换装置在额定频率下每周波20点采样，装置没有采样频率跟踪机制，因此当系统额定频率等于50Hz时，采样点间隔固定为1ms，其算法架构如图5所示。

图5 基于矢量修正的幅值算法架构算

下面以母线电压计算为例来说明算法实现。如上图所示，母线电压通道的20个采样点值经过带通滤波器处理后得到初始实部虚部：SIN(V_母线)，COS(V_母线)。当母线侧实际测量频率等于额定频率时，初始实部虚部就是准确值，无需修正，当母线侧实际测量频率不等于额定频率时，初始实部虚部与实际值有偏差，此时需要进行矢量修正。

矢量修正是根据母线侧实际测量频率对带通滤波器变换得到的初始实部虚部进行修正，不同频率偏差对应的修正系数是不同的，因此需要提供矢量修正系数表，这个表中的元素对应的是不同频率下的修正系数，中间频率对应的修正系数可以由插值算法得到。

矢量修正系数表是这个算法的核心部分，它直接关系到幅值计算的精度，因此如何得到矢量修正系数表是最关键的问题。得到矢量修正系数表的思路是首先根据式（6）和式（7）算出各频率段对应的实部和虚部的传递函数即响应系数

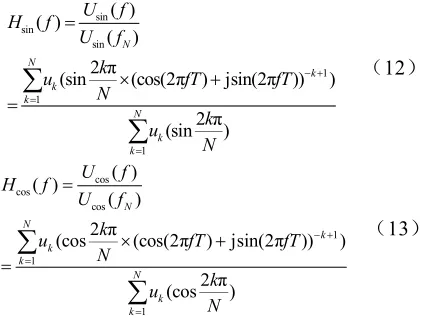
式（12）和式（13）中，f是实际电压电流的频率，T是采样点间隔。

然后求响应系数的倒数即推出矢量修正系数

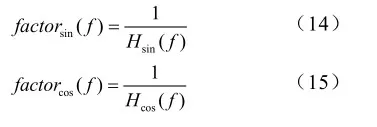
根据式（12），式（13），（14）和式（15）可算出各频率段对应的修正系数并做成矢量修正系数表。

母线侧频率可以由过零点算法得到，在此基础上查矢量修正系数表可得母线电压的修正系数：factor_SIN母线，factor_COS母线。矢量修正系数表的精度直接影响到幅值算法的精度，因此修正表的元素越密集，幅值算法的精度也就越高，当实际测量的母线频率不是整数而是介于修正系数表中元素的中间值时，可以用插值算法近似求得对应频率的修正系数。

在得到初始实部虚部以及向量修正系数后，就可以得到修正后的实部虚部：

4 基于矢量修正的幅值算法用于电源切换装置的优势

相对于传统幅值算法，基于矢量修正的幅值算法有以下优势：

（1）基于矢量修正的幅值算法对频率突变的响应速度快，提高快切的成功率和可靠性。

此算法不依赖于采样频率跟踪，电源切换装置的采样点频率将被固定为系统额定频率。此算法对频率突变的响应速度取决于向量修正对频率突变的响应，而向量修正采用查表法，只要新的频率被测量到，对应的向量修正系数就会得到，同时精确的实部虚部以及基波值也就会得到。另外，我们采用的频率算法是数据窗长度一个周波的过零点算法，频率测量的响应速度在一个周波以内，也就是说，基于矢量修正的幅值算法对频率突变的响应速度在一个周波以内，这个响应速度远远高于传统幅值算法的响应速度。

如图1所示工况，当工作电源侧发生故障而被切除时，母线侧频率会有一个1～2.5Hz的突变，之后会一直衰减下去直到被切换到备用电源。因此在工作电源刚被切除后的一个周波，实际母线频率就会被测到，同时精确的母线电压实部虚部以及基波值也就会得到。如果母线电压被用于快速切换判据，可以提高快切的成功率和可靠性。如图2所示工况，在工作电源刚被切除后的一个周波，精确的母线电流计算结果就会得到，大大提高了过流保护可靠性。

（2）取消采样频率跟踪机制可以降低电源切换装置CPU负载率。

当基于矢量修正的幅值算法应用于电源切换装置时，采样频率跟踪机制将被取消，相对于传统幅值算法可以省去至少两个中断源。中断源的减少会降低装置CPU负载率。

（3）取消采样频率跟踪机制会一定程度上减少频率和相角计算误差。

如前文所述，测频和测角差精度和过零点时标的计算有着直接关系。当采样点和过零点不重合时，我们需要用插值算法计算出过零点时标。插值算法是一种近似处理，也就是说，在过零点附近，我们认为两个采样点以及过零点是近似成一条直线的，很容易看出，采样点间隔越大，这种线性处理的误差也越大。取消采样频率跟踪机制后，当母线频率降低时采样点间隔仍然是固定的，这样就在一定程度上保证了插值算法的精确度，从而减小频率和相角计算误差。

（4）基于矢量修正的幅值算法的数据窗长度是固定的。

因为此算法数据窗固定为一定数量的采样点（比如20个采样点）而且采样点间隔是固定的，所以当母线频率下降到比较低时此算法数据窗长度仍然是固定的。

5 结论

随着机组容量的增大和自动化水平的提高，以往厂用电的切换方法已不能适应，一些新的切换模式和算法应运而生。基于矢量修正的幅值算法应用于电源切换装置中，可以大大提高装置对频率突变的响应速度，从而提高快切的成功率和可靠性，同时也克服了传统幅值算法带来的一些问题，保证了机组、电厂的安全运行，提高电网安全稳定运行的水平。

[1] Thomas R. Beckwith, Member, IEEE, and Wayne G. Hartmann, Member, IEEE.Motor Bus Transfer: Considerations and Methods.2006.

[2] Vinayagam Balamourougan, Member, IEEE, Tarlochan. S. Sidhu, Fellow, IEEE, Bogdan Kasztenny, Senior Member, IEEE, and Manish. M. Thakur, Member, IEEE Robust Technique for Fast and Safe Transfer of Power Plant Auxiliaries. 2006.

[3] 索南加乐, 宋国兵, 许庆强, 张健康, 赵志华.任意长度数据窗幅频特性一致的正交相量滤波器设计[J].中国电机工程学报, Proceedings of the Csee, 2003年06期.

[4] 张伏生,耿中行,葛耀中.电力系统谐波分析的高精度FFT算法[J].中国电机工程学报,1999,19(3):63-66.

[5] 袁宇波,陆于平,刘中平.基于相量法的短数据窗快速滤波算法[J].电力系统自动化,2004(3).

[6] 李经升,王舜,韩学义.厂用电快速切换装置的应用研究[J].继电器, 2002(7).

[7] 洪佩孙.电厂厂用电快切装置投切条件分析[J].电力自动化设备,2007(5).

[8] 艾德胜.以电流为判据的厂用电源快切原理及实现[J].电力自动化设备,2006(6).

[9] 张培杰,孙国凯,车长海,张宝志.关于厂用电源快切装置切换判据的探讨[J].电力自动化设备,2005(6).