基于RBF神经网络的工业取水量预测研究
2011-04-23褚桂红
褚桂红
(山西省水利水电科学研究院山西太原030002)
水资源短缺已成为制约我国工业发展的重要因素,而要实现经济的快速发展,就必须解决好水的供需关系。需水量预测是制订供水决策的重要参考目标,可为水资源规划和管理提供必要的依据。工业取水量预测可以采用BP神经网络预测模型,但该模型采用的是沿梯度下降的搜索求解算法,这就不可避免地存在收敛速度慢、容易陷入局部最优等缺陷。由Moody J和Darken C于20世纪80年代末提出的径向基函数(Radial Basis Function,RBF)神经网络[1]是一种典型的局部逼近人工神经网络,能够避免传统的BP神经网络的缺点,因而得到了更广泛的应用。本文建立了基于RBF神经网络的工业取水量预测模型,并以某市为例进行了研究。
1 RBF神经网络
径向基函数(RBF)神经网络是一种以函数逼近理论为基础的三层前馈网络,具有很强的生物学背景,也是当前国际学术界前沿研究领域,在模式识别、图像处理、预测预报、故障诊断、信号处理、优化计算、专家系统与人工智能等方面得到了广泛的应用[2,3]。
1.1 RBF网络结构
RBF网络的结构与三层BP网络相似,分为输入层、隐含层和输出层,如图1所示。输入层节点传递输入信号到隐层,隐层节点由像高斯函数那样的辐射状作用函数构成,而输出层节点通常是简单的线性函数。RBF网络的最显著的特点是隐节点的基函数采用距离函数,使用径向基函数作为激活函数。径向基函数关于维空间的一个中心点具有径向对称性,而且神经元的输入离该中心点越远,神经元的激活程度就越低,即径向基函数对输入信号在局部产生响应。函数的输入信号靠近函数的中央范围时,隐层节点将产生较大的输出,因此,RBF网络无论在逼近能力、分类能力和学习速度等方面均优于BP网络,能够避免局部收敛,实现快速全局收敛[3]。

图1 RBF神经网络结构图
1.2 网络原理
RBF神经网络的基本思想是:把径向基函数作为隐单元的“基”,构成隐含层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分问题在高维空问内线性可分[4]。径向基函数神经网络(RBF)是一种前馈神经网络,输入层节点只传递输入信号到隐层,输出层通常是简单的线性函数[5,7],隐层节点常由高斯函数构成。
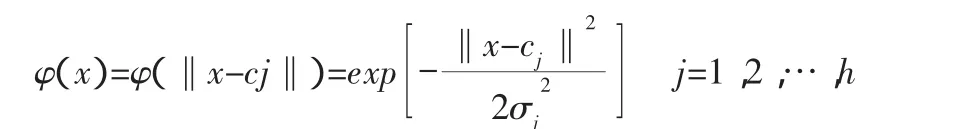
式中:x为n维输入向量;cj为第j个隐含层节点的基函数中心,与x具有相同的维数的向量;n是感知单元的个数,也就是隐含层节点的个数;σj为第j个隐含层节点的基函数宽度参数;‖x-cj‖为矩阵欧式范数,通常表示x与cj之间的距离;φ(x)在cj处有一个唯一的最大值,随着‖x-cj‖的增大,φ(x)会迅速衰减到零。
对于给定的输入,只有一小部分靠近x的中心被激活。设输入层的输人为(X=x1,x2,…,xj,…,xn),实际输出为(Y=y1,y2,…,yj,…,yM)。输入层实现从 X→φ(x)的非线性映射,输出层实现从φ(x)→yk的线性映射。

式中:Wjk为隐含层节点j至输出层节点k的链接权值;φj为隐含层节点的输出值;m为输出层节点数。
确定RBF网络的聚类中心cj、权值Wjk后,就可求出某一输入对应的输出值。
1.3 网络学习方法
从构造RBF网络的结构可以看出,构造训练RBF网络的过程,就是通过学习确定隐含层神经元的数目和每个隐含层神经元的中心、宽度以及输出权值的过程。根据径向基函数中心选择方法的不同,RBF网络有多种学习方法,其中随机算法和自组织学习算法适用于静态模式的离线学习,不能用于动态输入模式的在线学习,网络隐含层单元的节点数要事先人为确定,而最近邻聚类学习算法是一种在线自适应聚类学学习算法[8]。此算法隐含层单元节点数不需要事先人为确定,随着输入样本的变化,隐含层单元的节点数也随之而变,训练样本学习结束,隐含层单元的节点数随之确定下来。
2 基于RBP网络的工业取水量预测模型构建
影响工业取水量预测的因子很多,建立这些影响因子与取水量的精确数学模型较为困难,而神经网络具有广泛的从输入到输出的映射能力,是一种能够找到正确反映现实系统输人、输出及它们之间外在关系的有效工具。神经网络应用于预测领域,最普遍采用的是多层前馈神经网络模型,即BP网络。BP网络采用反向传播算法,不仅收敛速度慢,而且会遇到局部极小值问题,因此这里采用径向基函数(RBF)神经网络模型。
2.1 工业取水量影响因素分析
RBF神经网络工业取水量预测模型是建立在历年用水量的基础上,经过样本学习,确定网络模型结构,因此在进行取水量预测之前,应先对历年用水量进行分析。
工业取水量与用水户的生产规模、产业性质、技术水平、用水效率、用水定额等有关。通过对某市工业取水量变化规律进行分析,得到影响工业取水量的主要影响因素有:工业总产值、工业复用水量、工业总用水量、万元产值取水量、万元产值用水量、总复用率、排水量和耗水量8项指标,这些取水量预测影响因子与工业取水量之间呈复杂的非线性关系,要用精确的数学函数关系表达这样的非线性关系相当困难。RBF神经网络具有并行处理、容错性和很好的处理非线性问题等多种优良性能,可实现任意函数的逼近。基于RBF神经网络的工业取水量预测模型,通过对样本的学习,可以实现工业取水量预测影响因子与取水量预测的非线性映射关系。
2.2 数据归一化处理
采用某市1990-2000年共11年的资料,以1990-1997年8年的资料为训练样本,1998-2000年3年的资料为检验样本,训练前需对输入指标进行无量纲化处理,即数据的归一化。

式中:xi为归一化后输入或输出值;xi为输入或输出的样本值;xmax、xmin为样本数据中变化范围内的最大值和最小值。
3 预测结果及分析
根据资料条件,选用8个取水量预测因子作为径向基函数神经网络预测模型的输入,隐含层的节点数由最近邻聚类算法通过样本的学习确定,同时得到RBF网络连接权值,输出层输出工业取水量。训练前需对输入指标进行归一化处理,归一化后的样本数据见表1。

表1 归一化后的样本数据
预测模型中网络训练样本输入层节点数为8个,输出层节点数为1个,利用Matlab软件编程对网络进行训练,经过训练网络误差达到误差要求。用训练好的网络预测1998、1999和2000年的工业取水量,取水量预测因子见表2。

表2 工业取水量预测因子
利用训练好的网络对某市1998、1999和2000年工业取水量进行预测检验,预测结果见表3。由预测结果可知,RBF神经网络预测精度均高于BP神经网络,这说明RBF网络模型具有较高的预测精度,模型泛化能力强,可用于工业取水量预测等领域。

表3 模型预测结果
4 结语
本文利用RBF神经网络强大的非线性逼近能力建立了RBF神经网络取水量预测模型,该模型有较强非线性处理能力和逼近能力,采用最近邻聚类学习算法选取聚类中心,具有学习时间短、网络运算速度快、性能稳定等优点,避免传统BP神经网络容易陷入局部最优的缺点。
[1]Moody J and Darken C.Fast learning in networks of locally tuned processing [J].Neural Computation,1989(1):281-289.
[2]焦李成.神经网络系统理论[M].西安:西安电子科技大学出版社.1996:26-36.
[3]魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社,2005:46-73.
[4]高隽.人工神经网络原理及仿真实例[M].北京:机械工业出版社,2003:55-63.
[5]M J D Powell.Radial basis functions for multivariable interpolation:a review[C].J C Mason G Cox.Algorithms for approximation.New York:Clarendon Press,1987:146-167.
[6]C A Micchelli.Interpolation of scattered data Distance matrices and conditionally positive definite functions[J].Constructive Approximation,1986(2):11-22.
[7]刘旭,于国祥,沈西挺.基于神经网络德尔预测模型的比较研究[J].河北省科学院学报,2007(12):7-12.
[8]朱明星,张德龙.RBF网络基函数中心选取算法的研究[J].安徽大学学报(自然科学报),2000,24(1):74-78.
