基于可能度的坦克分队进攻战斗作战方案决策方法
2011-04-23徐亚军刘川禾
徐亚军,刘川禾
(蚌埠坦克学院,安徽 蚌埠 233050)
坦克分队进攻战斗作战方案的决策直接影响到坦克分队进攻作战的成败,甚至牵涉到战局的胜负。因此,这个问题受到了一些研究者的重视。2007年,朱英贵和赵建江研究了灰色定权聚类分析方法在坦克分队进攻作战方案决策中的应用,阐明了运用灰色聚类分析方法决策作战方案的几个重要环节和需要注意的问题,说明了该方法的具体应用,并证明了方法的可行性[1]。王全刚等运用模糊相似优先比法,对坦克分队作战中带有模糊性的作战方案进行解析计算,排出了各方案的优劣序列[2]。刁联旺等研究了基于博弈论的坦克分队进攻战斗作战方案评估模型,并给出了基于二人零和博弈求解最佳COA的举例[3]。2009年,徐大杰等针对坦克分队进攻战斗作战方案优选问题,提出了基于信息熵权的 TOPSIS决策方法[4]。该方法首先对原始数据计算熵权得到权重,然后与 TOPSIS方法结合进行定量分析,最后进行逼近理想解排序。
以上研究无疑对提高坦克分队进攻战斗作战方案决策的客观性、科学性、实用性和有效性做出了不同程度的贡献,但其决策方法中的属性值都是确定的实数值,而在实际作战中有些决策属性是不确定的区间数,如敌军的消耗数量、阵地夺占程度、队形疏散程度、己方兵力损耗等属性的准确值在作战之前我们根本无法预知,但可将其变换为评价分数并预估出分数的区间。显然,在决策属性值是区间数的条件下,再用确定的实数值进行决策,势必得出不正确的结果。为了解决这一问题,本文提出了基于可能度的坦克分队进攻战斗作战方案决策方法。
1 坦克分队进攻作战方案决策的基本概念
1.1 坦克分队进攻作战方案集、决策属性集与对应权重集
1.1.1 坦克分队进攻战斗作战方案集
假设一次坦克分队进攻战斗第i个作战方案为xi(i=1,2,…,n),那么由n个作战方案x1,x2,…,xn组成的集合可写成
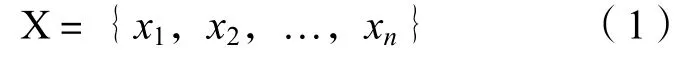
称为该次坦克分队进攻战斗作战方案集。
坦克分队进攻作战方案应依据我方作战目的、任务要求、目标特点、敌情、我情、地形、气候及电磁等相关环境条件拟定。
1.1.2 坦克分队进攻作战方案决策属性集与对应权重集
若对每个作战方案xi(i=1,2,…,n),都有m个决策属性(即评价指标)对应,则集合:

称为坦克分队进攻战斗作战方案集X的决策属性集。
在式(2)中,第j(j=1,2,…,m)个决策属性j为区间数[5]。


1.2 坦克分队进攻作战方案决策矩阵及其规范化
1.2.1 坦克分队进攻作战方案决策矩阵
由式(3)知,若第i个作战方案xi的第j个决策属性值用ij表示,则
式(4)中,ωj∈(0,1),且满足

据此可构造出n行m列的坦克分队进攻战斗作战方案决策矩阵:

1.2.2 坦克分队进攻作战方案决策矩阵的规范化

1)成本型属性规范化公式

2)效益型属性规范化公式

1.3 坦克分队进攻作战方案的综合属性值
对作战方案的各属性值进行加权集结,就可得到坦克分队进攻作战方案的综合属性值i(ω)。利用WAA算子[5]

可求得各作战方案的综合属性值
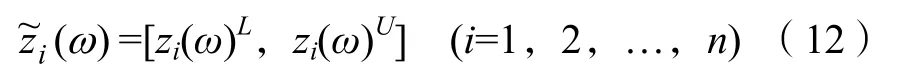
设作战方案xi和作战方案xj的综合属性值分别为i(ω)=[zi(ω)L,zi(ω)U]和j(ω)=[zj(ω)L,zj(ω)U],(i=1,2,…,n;j=1,2,…,n),若记la=zi(ω)U-zi(ω)L,lb=zj(ω)U-zj(ω)L,则i(ω)≥j(ω)的可能度[5]定义为
1.4 坦克分队进攻两作战方案比较的可能度

1.5 坦克分队进攻战斗n作战方案的可能度矩阵
对于计算出的坦克分队进攻战斗n个作战方案的综合属性值1(ω),2(ω),…,n(ω),利用式(13)将它们两两比较,求得相应的可能度p(i(ω)≥j(ω)),简记为pij,i=1,2,…,n;j=1,2,…,n。由此得到坦克分队进攻战斗n作战方案比较的可能度矩阵[5]:

该矩阵包含了所有作战方案相互比较的全部可能度信息,因此对综合属性值i(ω)(i=1,2,…,n)的排序,可用可能度矩阵P的排序向量进行。
1.6 坦克分队进攻作战方案可能度矩阵P排序向量
坦克分队进攻作战方案可能度矩阵P排序向量为
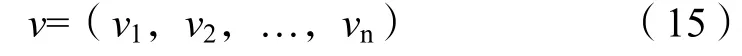
式中第i个分量的计算公式[5]为

利用式(15)和式(16)可对n个作战方案的综合属性值1(ω),2(ω),…,n(ω)进行排序,也就是对坦克分队进攻战斗n个作战方案排序。
2 基于可能度的坦克分队进攻作战方案决策步骤
步骤2 用Delphi法或两两比较法[6]求得权重集Ω;
步骤3 依据决策属性数据对各决策属性进行打分(分数在1~10之间),构造决策矩阵;
步骤5 利用式(11)和式(12)求得各作战方案的综合属性值i(ω)(i=1,2,…,n);
步骤6 利用式(13)和式(14)求得坦克分队进攻战斗n个作战方案两两比较的可能度pij,构建可能度矩阵P;
步骤7 利用式(15)和式(16)求得可能度矩阵P的排序向量v,并利用v对n个方案进行排序,即可得到最优的决策方案。
3 基于可能度的坦克分队进攻作战方案决策示例
在对某坚固阵地防御之敌的进攻战斗中,红军某坦克连长综合各方面因素构建了有五套作战方案的作战方案集 X={x1,x2,x3,x4,x5},评价这五套作战方案的属性定为6个:1为消耗的敌人数量;2为发起冲击的时间差;3为完成任务的时间;4为阵地夺占程度(推进距离);5为队形疏散程度;6为兵力损耗,决策属性集={1,2,3,4,5,6}。利用两两比较法求得权重集Ω={0.20,0.14,0.18,0.15,0.14,0.19}。
红军坦克连长综合各方面因素对五套作战方案的各项属性进行打分,构造得出决策矩阵为:

2 13456 x1 [5,6][6,8][6,7][4,6][7,8][8,10]x2 [6,8][5,7][8,9][7,8][4,7][7,8]x3 [5,7][6,7][8,10][7,9][5,7][6,7]x4 [8,10][5,6][4,7][5,7][6,8][4,7]x5 [8,10][6,7][5,6][6,9][4,7][5,8]

2 13456 x1 [0.268,0.410][0.371,0.636][0.338,0.489][0.227,0.454][0.400,0.605][0.443,0.725]x2 [0.321,0.547][0.338,0.580]x3 [0.268,0.479][0.309,0.557][0.451,0.629][0.397,0.605][0.228,0.529][0.332,0.508]x4 [0.428,0.684][0.371,0.557][0.451,0.698][0.397,0.680][0.285,0.529][0.309,0.477][0.225,0.489][0.284,0.529][0.342,0.605][0.222,0.508]

x5[0.428,0.684][0.371,0.636][0.282,0.419][0.340,0.680][0.400,0.680][0.277,0.580]
利用式(13)和式(14)计算求得5套作战方案两两比较的可能度pij,构建可能度矩阵P如下:

利用式(15)和式(16)计算出可能度矩阵P的排序向量为:
v=(0.1943,0.2053,0.2031,0.1855,0.2118)
由排序向量v得到5套作战方案综合属性区间数i(ω) (i=1,2,…,5)的排序为


决策结果:最优作战方案为x5。
4 结束语
本文将不确定属性决策理论和方法应用于坦克分队进攻战斗作战方案的决策,提出了一种基于可能度的坦克分队进攻作战方案决策方法,解决了在决策过程中由于决策属性值是区间数而导致的不确定性问题。研究表明,该法特别适用于决策属性值为区间数而权重为确定实数的情况。而决策属性值及其权重都是区间数的情况还有待进一步深入研究。
[1]朱英贵,赵建江.灰色定权聚类分析在作战方案决策中的应用[J].火力与指挥控制,2007,32(8):130-132.
[2]王全刚,赵以贤,辛卫锋,等.模糊相似优先比拟法在坦克分队作战方案优选中的应用[J].射击学报,2007(3):35-36.
[3]刁联旺,赵鲁宁,魏太平.基于博弈论的坦克分队作战方案评估[J].射击学报,2007(3):17.
[4]徐大杰,王永彬,薛剑.基于熵权的坦克分队作战方案优选[J].兵工自动化,2009,28(4):48-50.
[5]徐泽水.不确定多属性决策方法及其应用[M].北京:清华大学出版社,2004.
[6]汪应洛.系统工程理论、方法与应用[M].第 2版.北京:高等教育出版社,1998.
