塔影效应引起的风电机组输出功率波动问题

张弘鲲,孟祥星

（1.华北电力大学,北京 102206;2.黑龙江省电力有限公司,黑龙江 哈尔滨 150090）

由于风电机组的输出功率与风速的3次方成正比,而风速具有随机变化的固有特性,因此,风电机组的功率输出也是不稳定的,这种不稳定的功率注入电网,尤其是在大规模风电场并网的情况下,将对电网的稳定性和电能质量造成影响。对风电机组输出功率的波动性进行研究,不论从维持系统稳定还是从保证电能质量的角度都具有实际意义。

风电机组输出功率的波动来源于风电机组运行过程中非恒定的转矩,该转矩的不稳定不但与风速的变化（如阵风、渐变风等）有关,而且还受机组自身固有特性的影响（如塔影效应、偏航误差及风剪切作用等）,严重时这些因素将使风电机组的转矩偏差达到20%[1、2],并且风电机组输出功率的波动周期与叶片旋转周期具有对应关系[3-5]。对于3叶片风电机组来说,转矩的波动频率是叶片旋转频率的3倍,由此引起的输出功率波动频率也是叶片旋转频率的3倍。

为从理论上对由于塔影效应和风剪切引起的风电机组输出功率波动性进行分析,建立了相应的风速模型和风电机组模型,但多数文献对此进行描述时,仅定性说明了这些作用对风速的影响,或建立了含有一些经验参数的极坐标下的风速模型[1],不具有普遍适用性。因此,结合其他文献的研究成果,建立了描述塔影效应和风剪切效应的风速模型,并结合某恒速风电机组数据和相关模型,对风电机组输出功率的波动问题进行了计算分析。

1 风速模型

风电机组是将风能转换成电能的中间环节,对风速的准确描述是研究风电机组输出特性的基础工作之一。鉴于本文的研究目的,仅为说明塔影效应和风剪切等作用对风电机组功率输出的影响问题,将机组轮毂高度处的自然风速视为已知的恒定值,而将风电机组各叶片在塔影效应和风剪切作用下的等效风速作为输入量进行分析,等效风速用于产生风力机的机械力矩。

风力机的叶片在旋转过程中,在不同的位置处所面对的风速是不同的,这是风速垂直梯度变化的结果。风速在垂直方向上的变化也称为风剪切,可表示为

式中 H——风电机组的轮毂高度;

z——距离地面的高度;

v（H）、v（z）——分别表示机组轮毂处和距离地面高度z处的风速;

α——风剪切指数。

虽然可以根据地表粗糙程度对α进行数学描述,但一般都是通过实测求出其大小。实测表明指数α并非常数,而是随时间、风速及温度的变化而变化,有时还会出现负值[3、4],这种变化将影响风电机组输出功率。本文模型中将α视为正的常数。

风剪切对轮毂高度处等效风速的影响可按公式（2）计算[4]：

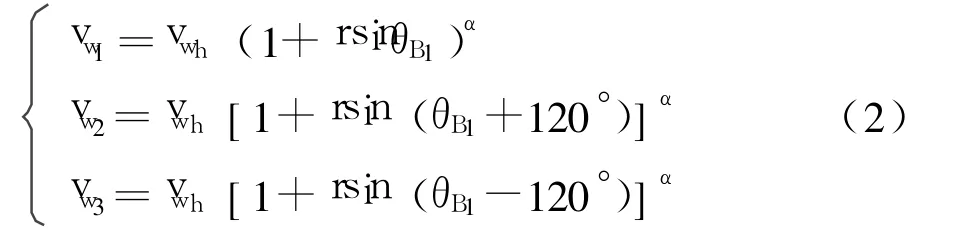
式中 vwh——轮毂高度处的风速,认为是常数;

vw1、vw2、vw3——分别为1号、2号、3号叶片风速;

θB1——1号叶片的旋转角度,是时间的函数;

r——轮毂到叶片顶端3/4距离与轮毂高度

之比。

由于塔筒的影响,风在经过塔筒时会产生风向和风速的改变,进而造成风力机转矩的变化,这种效应就是塔影效应。塔影效应对叶片的影响可以等效为叶片经过塔筒时风速的降低[6],其示意图如图1所示。其中θB表示叶片的旋转角度,2δ为受塔影效应影响的角度范围,Δvw为风速的降低量。考虑塔影效应后,每个叶片经过塔筒时都将产生一个降低的风速,此时等效轮毂高度处的风速表示为v′w1、v′w2和v′w3。在风力机倾角为5°时塔筒前的风速约降低30%,而随着倾角的减小风速有所降低。受塔影效应影响的角度约在60°以内[7]。本文风速模型中将这2个量分别取为30%和60°,并假定风速的降低符合正弦规律变化。

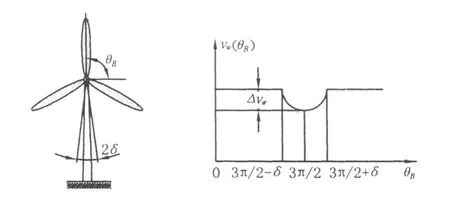
图1 塔影效应的等效风速示意图

通过上述分析可以看出,风电机组3个叶片的等效风速都是叶片旋转角的函数,随时间而变化。轮毂高度处的等效风速可表示为

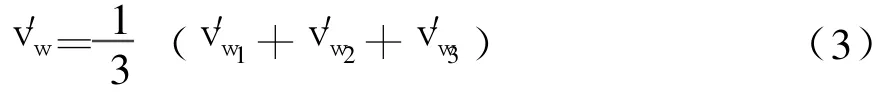
相应的转矩可由公式（4）计算

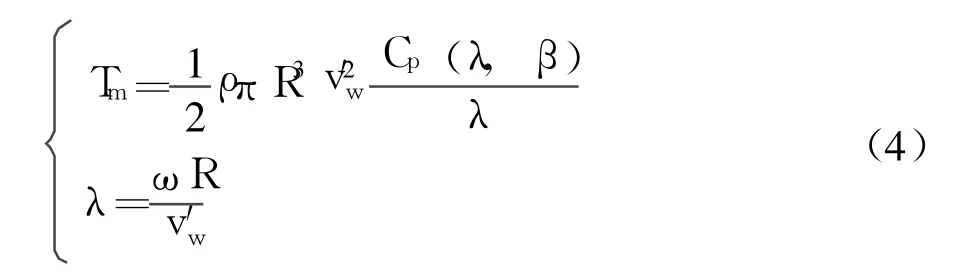
式中 ρ——空气密度;

λ——叶尖速比;

R——叶片旋转半径;

ω——叶片旋转角速度。

功率系数Cp与叶尖速比λ及桨距角β有关。

式（2）、式（3）及图1构成了含有塔影效应和风剪切效应的风速模型,可以看出等效风速v′w随叶片旋转角变化而变化,因此,转矩也是随叶片旋转角变化而变化。

2 算例分析

为便于对风剪切和塔影效应影响的理解,以额定容量500 kW的MADE-AE41型风电机组（恒速）为例进行分析,有关参数如表1所示。

表1 MADE-AE 41型风电机组的风力机参数

对于每个平均风速,都有一个平衡转矩与其对应,即风电机组在该风速下的电磁转矩和机械力矩达到平衡。MADE-AE41型风电机组的平衡转矩与风速关系曲线如图2所示[1]。

图2 平衡转矩与风速关系曲线

根据风速模型编制考虑塔影效应和风剪切效应的等效风速计算程序及图2曲线的拟合函数形式,可以计算出不同效应下的风速变化规律及不同平均风速下风电机组的转矩变化。假定风剪切指数为典型值（α=1/7）,并取轮毂高度处的自然平均风速为v=10m/s,计算得到的单叶片风速的变化曲线如图3、图4所示。

图3为仅考虑风剪切后的单叶片风速变化规律,图4为同时考虑风剪切和塔影效应后的单叶片风速变化规律。可以看出,塔影效应对作用到叶片上的风速的影响要比风剪切的作用大得多,风速的变化主要来源于塔影效应。

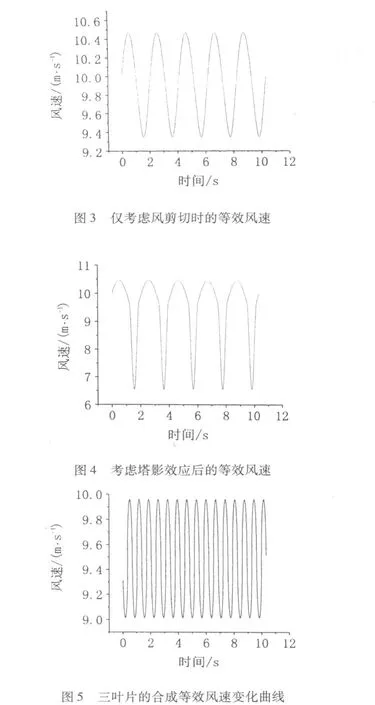
三叶片的合成风速如图5所示,与单叶片相比三叶片合成风速的波动幅度有所降低,而波动频率增大为原来的3倍,即达到3p频率;同时总的等效平均风速也有所降低,约达到v=9.5 m/s。因此,风剪切和塔影效应不但使风电机组输出功率产生波动,而且还将使总的输出功率降低。根据图2曲线可以看出对应v=9.5m/s时的转矩约比v=10 m/s时降低10%,即风电机组的输出功率也有约10%的损失。

需要指出的是,本文仅是用风电机组的平衡转矩与平均风速的关系曲线对由于风速的变化造成的输出功率降低进行估计,详细的计算应该是建立风电机组的动态模型,结合本文风速模型可以得出相对精确的功率变化规律。

3 结论

a.本文考虑塔影效应和风剪切作用后的等效风速模型,可以用于风电机组输出功率的仿真计算,计算结果准确程度与风电机组类型及其模型有关。

b.塔影效应对风电机组输出功率的影响比风剪切作用大很多,风电机组输出功率的波动主要来源于塔影效应。

c.风剪切和塔影效应使恒速风电机组的输出功率产生3p频率的波动,且在数值上降低一定幅度。

[1] H.Armaris,C.Vilar,et al.,Frequency domain analysis of flicker produced by wind energy conversions systems,Paper accepted for presentation at the 8thinternational conference on harmonics and quality of power ICHQP'98,jointly organized by IEEE/PES and NTUA,Athens,Greece,October 14-16, 1998.

[2] Carolina Vilar Moreno,Hortensia Amaris Duarte,Julio Usaola Carcia,Propagation of flicker in electric power networks due to wind energy conversions systems,IEEE Transactions on energy conversion,Vol.17,No.2,June 2002.

[3] Torbjörn Thiringer,Jan-Åke,Dahlberg,Periodic power pulsations from a three-bladed wind turbine,www.elkraft.chalmers.se/Publikationer/EMKE.publ/Abstracts/A lsvik.pdf.

[4] Stephen B.Bayne,Michael G.Giesselmann,Effect of blade passing on a wind turbine output,Release A：Copyright 2000 by the American Institute of Aeronautics and Astronautics.

[5] M.Davidson,Interaction of a wind farm with the distribution network and itseffect on voltage quality, 1996 the institution ofelectrical engineers,Printed and published by the IEE,Savoy Place,London WC2R OBL.UK.

[6] M.P.Papadopoulos,S.A.Papathanassion,et al.Investigation of the flicker emission by connected wind turbines,Paper accepted for presentation at the 8thinternational conference on harmonics and quality of power ICHQP'98,jointly organized by IEEE/PES and NTUA,A thens,Greece,October 14-16,1998.

[7] John Olav Giæver Tande,Giorgos relakis et al.,Synchronisation of wind turbines,Wind power for 21stcentury,25-27 Sept.2000,Kassel,germany,Subject number：3,www. energy,sintef.no/prosjnyt/levkval/vindkrft/sync_paper01.pdf.

[8] Andres E.Feijoo,Jose Cidras,Modeling of wind farms in the load flow analysis,IEEE transactions on power systems,Vol. 15,No.1,February 2000.