压力管道空间弯管转角计算的两种方法

庞 江

(四川南充水利电力建筑勘察设计研究院,四川 南充,637000)

石绵方大坪电站压力管道主管,布置于桩号为0+000.000～0+252.460m,内径4.8m,其中在桩号0+000.000～0+015.676m处为明管,在0+015.676m～0+252.460m处为埋管。主管转点共三个,其中两个为空间转点,需要计算其空间转角。本文以此为例介绍空间转角的两种计算方法,即用向量法求空间转角及利用AUTOCAD作图法求空间转角。

1 向量法求空间转角

同理,若空间三点A2,B2,C2座标分别为:

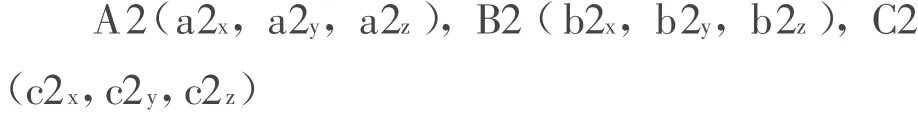
则:空间三点A2,B2,C2组成的平面∏2的法向n2为:

则:平面∏1法向量n1=(μxρi,μyρj,μzρk):

平面∏2法向量n2=(vxρi,vyρj,vzρk)

则平面∏1和∏2夹角θ的余弦为:

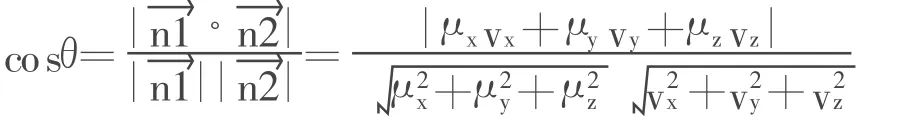
现以石绵方大坪电站压力管道空间弯管为例,说明利用向量法计算空间弯管转角θ的计算方法。

压力管道管线图见图1,E0为前池处压力管道起点,E1为第一个空间弯管转点,E2为第二个空间弯管转点。现以E1点为例进行说明。

根据水工平面图,可得E0、E1、E2的空间坐标为:

E0 (3257145.1152,34515535.0044,1163.5500)

E1 (3257154.1806,34515536.6634,1163.5500)

E2 (3257211.0753,34515606.5274,1132.5000)

过E2点作一线段垂直于直线E1E2,线段的端点为E22(线段长度任意),E22的高程为1132.50m,根据平面图可求得E22的空间坐标为EE2(3257288.6158,34515543.3812,1132.5000),由几何关系可知E0、E1、E2组成的平面与E1、E2、E22组成的平面的夹角,即为本段空间弯管的空间转角。

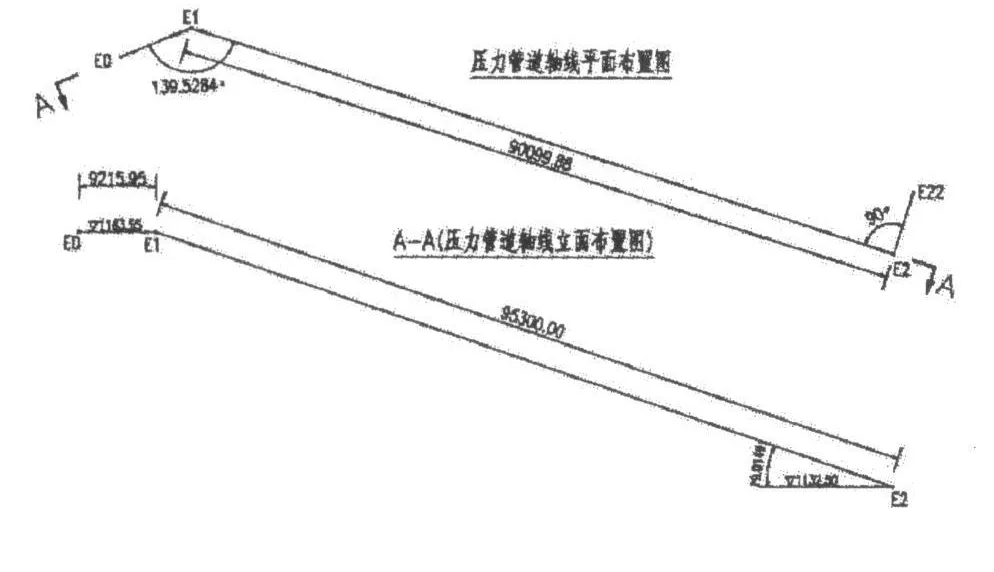
图1

由上述向量法可知:

由此可求得空间转角为:20.9001°

通过此方法,还可以求出空间任意两条相交直接、一条直线和一个平面的相交的夹角。

2 作图法求空间转角

首先在AUTOCAD绘图空间中输入E0、E1、E2、E22四点的坐标,组成以下图形(图2)。

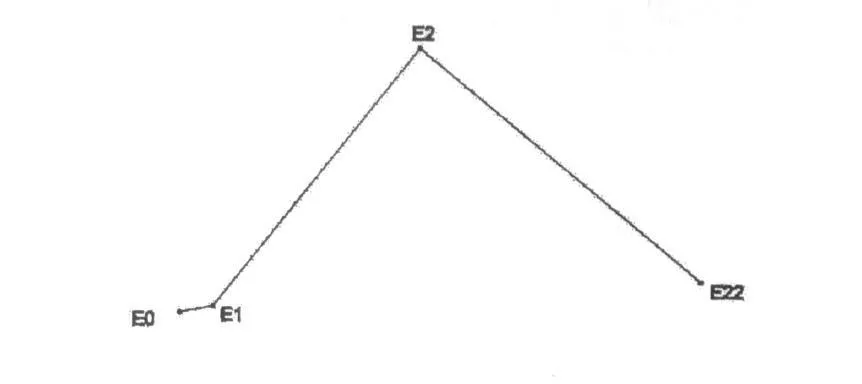
图2

由图2可知,点E0、E1、E2组成的平面和点E1、E2、E22组成的平面的夹角即为空间转角。这两个空间平面的相交线为E1E2,那么过E22作交线E1E2的垂线,过E0作交线E1E2的垂线,则这两条垂线的夹角即为空间转角。由于E1E2⊥E2E22,将过E0点垂直于E1E2的直线E0E0′进行移动,使点E0′和E2点重合,则移动后的直线E0E0′和E2E22的夹角即为空间转角,如图3所示:

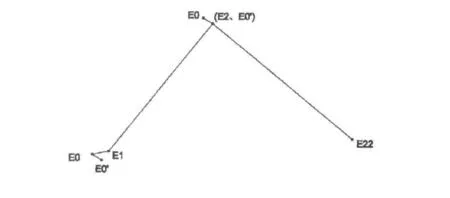
图3

在AUTOCAD中,将坐标平面转换为直线E0E0′移动后形成的由点E0、E2、E22组成的平面,直接量测得到空间转角为20.9001°,见图4。

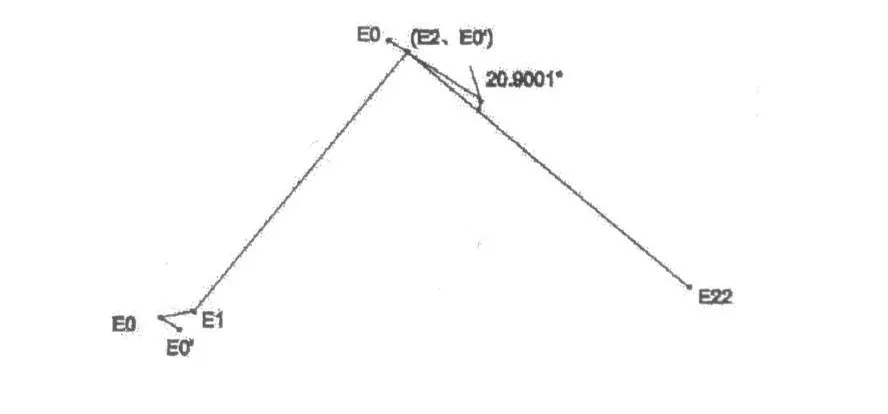
图4

3 结语

由上述可见,使用作图法和向量法求得的空间转角是一致的。使用作图法求空间转角较为形象且直观,而向量法便于编写程序,由计算机完成计算。由于目前计算机的使用基本已经普及,建议使用向量法编写程序,由计算机自动完成空间转角的计算,快速而准确。