线状地图符号数学定义的研究以及实现
2011-04-18杨涛张剑锋
杨涛,张剑锋
(1.兰州交通大学数理与软件工程学院,甘肃兰州 730070; 2.兰州市勘察测绘研究院,甘肃兰州 730050)
线状地图符号数学定义的研究以及实现
杨涛1,2∗,张剑锋2
(1.兰州交通大学数理与软件工程学院,甘肃兰州 730070; 2.兰州市勘察测绘研究院,甘肃兰州 730050)
地图符号qgf(x)是制图对象x在f,g,q三重拓扑映射下的象[1]。在此基础上,通过分析地图线状符号的特征,提出了半依比例线状符号的数学定义,并给出了对构造矢量线状符号的几何图元进行旋转、变形、裁剪等处理方法的数学基础,且运用面向对象的方法给出了线状符号的实现过程,最终通过实现证明了该方法解决了拐点超出扇形区域的问题且在视觉上达到了很好的效果。
地图符号;线状符号;数学定义;面向对象
1 引 言
地图符号是表达空间地理信息所用的极其特殊的语言符号系统,具有严格的数学基础、精确的空间位置和可量测性。也可以认为地图符号是概念符号的集合,因为所有地图符号都是描述空间地理事物和现象某方面的特征。钟业勋、魏文展、黄鹄等从数学的角度提出了点状、线状、面状地图符号的数学定义[1];还给出了依比例、不依比例、半依比例地图符号的严密数学定义[2],但仅考虑了少量符号变量且以二维地图模型为基础,难免存在一些不足。何忠焕从线状单元的衔接、特殊位置成员、符号的异常等方面提出复杂线状符号的绘制[3],但该填充方法存在一定的不足。当拐点角度在一定范围内时,拐点在扇形区域的外部。计算线状符号外接矩形顶点的坐标时,要依靠前面的拐点角度,从而使得重复计算太多,增加计算复杂性等。本文在此研究的基础上,给出了更为广泛的半依比例线状符号的数学定义,并给出了对构造矢量线状符号的几何图元进行旋转、变形、裁剪等处理方法的数学基础以及运用面向对象的方法实现了符号化。
2 线状符号的理论分析
线状符号表示空间上的一维地物和地理现象,长度在图上依比例尺表示,而宽度在图上不依比例尺表示。例如围墙、一般铁路、加固斜坡等,线状符号一般都有如下特征:
(1)都有一条有形或无形的定位线。
(2)都可以分解成基本线划单元(可称之为基线)和结点描述信息的复合,形成线状地图符号基本图元,这种图元呈周期性变化。
(3)一个基本线划单元通常包含3种结点信息,即可在基本线划单元的首、中、末位置上配置结点信息(点状符号描述)。
例如,对于地图符号铁路和围墙,如图1,图2所示。

图1 铁路符号

图2 围墙符号
3 线状符号的数学定义
3.1 地图符号的一般定义
根据拓扑映射原理,得地图符号的一般定义。
定义1[1]:设x∈A⊆X是三维空间X中制图区域A内的制图物体。存在从三维空间X到地球椭球面S的映射f:X→S和地球椭球面S到制图者的认知结构Y的映射g:S→Y以及从制图者的认知结构Y到二维平面Z的映射q:Y→Z。x在f,g,q三重拓扑映射下的平面像qgf(x)∈qgf(A)⊆Z称为制图物体x的地图符号。
同理,将用映射q1代替映射q,可得计算机数码集Z1中的数字地图符号q1gf(x)∈q1gf(A)⊆Z。若引入时间变量,则得动态地图符号,其集合便构成动态地图。
3.2 半依比例符号的一般定义
定义2[2]:设qgf(x)是x在f,g,q三重拓扑映射下的地图符号,在1∶M比例尺条件下,若对于∀P∈qgf (x),∃Pα,Pα∗∈qgf(x)使得:
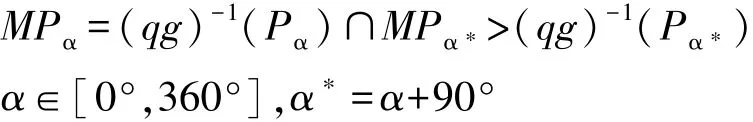
则称qgf(x)为x的半依比例符号。其中α为依比例方向,α∗为不依比例方向。
3.3 半依比例线状符号的定义
线状符号的图案大部分是由周期性出现的基本图元串接而成,运用线状符号的可分解性,将线状符号分解为多个基本图元,并按顺序分别从符号的起点到终点绘制出各图元,从而实现线状符号的绘制。此方法需要记录各图元之间的相对位置,确定各图元之间的位置依赖关系。因此,可认为线状符号的图案是由基本线划单元和结点信息(点、直线段、折线段、样条曲线、多边形、曲边形、矩形、椭圆、椭圆弧、弓形、扇形、星形、文字、位图等)复合并呈周期性变化。由此可得:若在1∶M比例尺条件下,线状符号的数学描述如下:

其中:L—表示线状符号;M—表示线状符号的比例尺;qgf—表示线状符号的生成函数;S—表示基本图元;(X,Y)—表示基本图元坐标串;T—表示线状符号周期长度。

其中:S表示基本图元;Xi,Xk表示基本线划单元或结点;R表示基本线划单元或结点Xi,Xk之间的位置依赖关系;Yj表示基本线划单元或结点描述信息的属性。
则称L为制图物体x的线状符号。
简化线状符号的书写形式为:

若对于∀L1∈L∗,∃L1α,L1α′∈L∗使得:
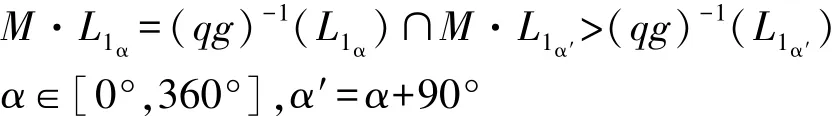
则称L为制图物体x的半依比例线状符号。其中α为依比例方向,α′为不依比例方向。
4 线状符号填充描述
文献[3]从线状单元的衔接、特殊位置成员、符号的异常等方面提出复杂线状符号的绘制,此绘制方法存在一定的不足。当两个符号图元拐点角度在一定范围内时,将出现拐点在扇形区域外部,这时必须计算线状符号外接矩形顶点的坐标,而计算这个坐标将依靠前面所有的拐点角度和拐点的坐标,以至重复计算太多,增加计算复杂性等。为此,本文在文献[2,3]的线状符号填充算法的基础上,对于这些不足做了有效的改进。
任意给定的一条线状要素的定位线,其填充规则可描述为:第一步线状符号图元的旋转处理(如图3的AB段、FG段),第二步线状符号图元的变形处理(如图3的BCD段、DEF段),第三步线状符号图元的裁减(如图3的GH段)处理,以达到线状符号的形状和长度。
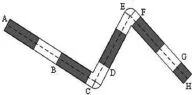
图3 线状符号填充
根据上述填充规则的描述,结合线状符号横向循环配置的方法,得到以下线状符号填充的详细过程。
4.1 计算基本图元的个数
线状符号填充处理首先确定填充的直线段,然后计算其有效长度,根据长度来确定可以填充完整的基本图元数目。令:

其中,d—表示基本图元的长度;Li—表示线状符号定位线的分段长度;li—表示与图元相邻的上一个图元填充后被裁剪转入本直线段的图元长度;且l1=0;ni—表示每一条直线段填充的完整基本图元的个数;mi—表示每一条直线段填充的基本图元所剩余的长度;i表示线状符号基本图元的个数。
以上图为例,按照上述方法填充有:
第一条直线段的长度:L1=AC;
完整填充的基本图元个数:n1=(L1-li)/d;l1=0基本图元填充后剩余长度:m1=(L1-l1)%d
转入下一条直线段的剩余基本图元长度:l2=d-m1
这样一直下去就可以求出所有直线段上可完整填充的基本图元个数。
4.2 旋转处理
旋转处理指以被填充线状符号的起始点作为旋转点,将同一条直线段上的所有基本图元旋转适当的角度,以满足线状符号填充的需要。
(1)旋转角度的表达方法
在线状符号旋转处理中规定:旋转角度θ∈(-180°,180°),取逆时针旋转的角度为正。根据两条直线段的所得的向量,记作:通过向量的数性积,求取拐点旋转角度的大小,而由向量矢性积,求得拐点旋转角度的正负,计算公式如下:

(2)旋转的坐标变换计算方法
设(x0,y0)为初始点,(x1,y1)为旋转后的点,旋转角度为θ,则坐标变换公式为:
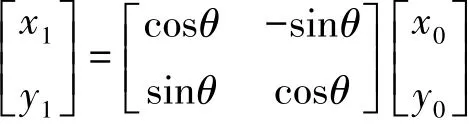
运用上述的旋转处理规则,可以对图4进行简单线状符号旋转处理,从而使线状符号的方向和定位线的方向一致。
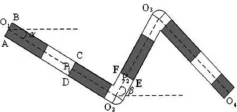
图4 线状符号的旋转
首先假设定位线的拐点分别为O1、O2、O3和O4,坐标分别为:O1(x1,y1)、O2(x2,y2)、O3(x3,y3)、O4(x4,y4),线状符号基本图元的高度为h,长度为d,第一次旋转角度为α,建立线状符号定位线的坐标系,线状符号(如图4的矩形ABCD)在旋转之前,其顶点坐标分别为A(xA,yA)、B(xB,yB)、C(xc,yc)、D(xD,yD),其中xA=xB=x1、xC=xD=x1+d、yA=yD=y1-h/2、yB=yC=y1+h/2。
线状符号定位线绕拐点O1(x1,y1)旋转角度α。A、B、C、D四个点以同样的处理旋转,以(x,y)代表A、B、C、D四点的坐标,旋转后的新坐标为(x′,y′),则有如下变换:

而对于其他线状符号定位线也一样相同方式处理。
4.3 变形处理
变形处理主要应用于基本图元填充时遇到拐点外侧出现的断裂情况,此时线状符号的基本图元填充到拐点(如图5的O2)时和下一条直线段开始的基本图元之间的断裂部分用扇形(O2GH)填充。
扇形O2GH的顶点坐标很好求得,O2为坐标已知的拐点,而点G和H也是拐点前后两个基本图元的顶点坐标。扇形颜色的填充将分为两步进行,第一步应用拐点角的角平分线将扇形划分为两个区域;第二步对两个区域用与之相邻基本图元符号的颜色进行填充。其他的扇形处理方式同上。
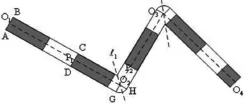
图5 线状符号的变形
4.4 裁减处理
裁减处理解决的是拐点位置的符号重叠和交叉现象。裁剪最后一条直线段填充的线状符号基本图元和拐点相邻的两个线状符号基本图元与拐点角平分线相交的多余线状符号基本图元。
5 实现
5.1 实现机制
利用面向对象技术设计合适的图形元素类(以下简称图元类),特定的图元类对象不仅可以描述一个图形元素,而且它应具有一定的行为。这样图元类就是具有智能的最小功能单元。通过类的继承,使得不同的图元类都具有共有的行为方法,再利用面向对象语言的多态性对特殊的类设计特殊的行为。这样不仅提高了图形的编辑效率,而且在很大程度上方便了整个工程的编程。例如在图元类中修改自身属性的方法,这样系统在接到编辑图形消息时,只需将编辑消息传送到相应的图元类对象的相应接口就可以了,而没有必要直接修改图形元素的属性参数。图元类对象修改了属性后,再使用绘制方法(Draw)将所描述的图形在界面上重绘。为此图元类应有以下基本要求:
(1)图元类必须完全描述基本图形元素(以下简称为图元),即包含描述这种图元的所有属性参数;
(2)能够接受用户对图元的编辑消息,能够实现对图元的编辑功能,如对图元属性的修改,自我复制等;
(3)将自身描述的图元,记录到文件的功能,即用GDI+绘制图元写进元文件中的功能。
5.2 实现过程
为了方便编程,实现代码的重用,采用以下继承关系,如图6所示。

图6 线图元类的继承图
(1)最上层是CGraphElement,此类具有线状图元类的共同属性,如光栅操作模式、选中状态标识、图层索引号等,另外还具有图元类都具有的方法和外部接口;
(2)中间层是CLineELement,此类为线状元素的基本图元类,具有本图元的私有属性及方法,如CLine描述一条直线,具有私有属性直线的起点、终点等。
(3)特殊的图元类说明
①CInsertBmp类,处理位图图片类。该类具有处理元文件中记录的位图图片的所有属性和方法,如位图大小、位置、类型等属性以及处理位图的对比度、明亮度等方法。
②CComboDraw类,组合图元类。此类具有支持图元的组合、分解等操作而设计的特殊图元类。在该图元类中有一个CObaray类型的私有成员变量,在此变量中存有一个或多个图元对象,再这些图元对象中,可能存在CComboDraw类型的对象。整幅矢量图形可以看成一个大的组合类型图元对象,因此一幅矢量图形用图元对象表示,则是一棵树型结构,如图7所示。

图7 组合图元的树形结构
6 实验与结论
本文在分析已有GIS与地图制图软件设计地图符号的基础上,提出了线状符号的数学定义,运用Arc-GIS Engine和C#,以线状符号图案周期性理论为依据,设计了一种面向对象的线状符号编辑器。在符号化过程中,解决了线状符号填充时,拐点出现的符号交叉、重叠、断裂、空白等失真现象,通过对线状符号的填充、旋转、变形、裁减等方法的处理,有效防止了失真现象,不仅解决了拐点超出扇形区域的问题,而且在视觉上达到了很好的效果,最重要的是解决了基本图元重复计算的问题,提高了线状地图符号符号化的效率(图8、图9为符号图元和线状符号填充示意图)。

图8 符号图元

图9 线状符号填充示意
[1] 钟业勋,魏文展,彭月英等.地图符号数学定义的研究[J].武汉大学学报·信息科学版,2001,26(5):465~468
[2] 黄鹄,钟业勋.依比例符号、不依比例符号和半依比例符号数学定义的改进[J].武汉大学学报·信息科学版,2006,31(3):244~246
[3] 何忠焕.GIS符号库中复杂线状符号设计技术的研究[J].武汉大学学报·信息科学版,2004(2):132~134
[4] 钟业勋,黄鹄.依比例、不依比例和半依比例符号数学定义的修改[J].海洋测绘,2008,28(4):19~21
[5] 魏文展,钟业勋,彭月英等.点状、线状和面状地图符号数学定义的研究[J].武汉大学学报·信息科学版,2002,27 (4):424~426
[6] 钟业勋,郑红波.不同约束条件下地图符号的数学定义[J].测绘信息与工程,2007,32(3):69~70
[7] 钟业勋,朱重光,魏文展.地图空间认知的数学原理[J].测绘科学,2005,30(5):11~12
[8] 黄鹄,钟业勋.点线面地图符号定义的简化与统一[J].测绘科学,2005,30(6):69~70
[9] BRIVIO P A,GIARDINO C.Determination of chlorophyll concent ration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images[J].Int.J.RemoteSensing,2001,22(223):487~5021
[10] DOXARAN D,FROIDEFOND J M.Spect ral signat ure of highly turbid waters application wit h SPOT data to quantify suspended particulate matter concent rations[J].Remote Sensing of Environment,2003,81:149~1611
[11] 胡最,闫浩文.地图符号的语言学机制及其应用研究[J].地理与地理信息科学,2008,24(1):17~20
[12] 谈晓军,边馥苓,何忠焕.地图符号可视化系统的面向对象设计与实现[J].测绘通报,2003(1):11~14
[13] 沈陈华.线状符号库的面向对象设计[J].重庆师范学院学报:自然科学版,2000,17(4):41~43
[14] 张海泉,潘懋,吴焕萍等.面向GIS的矢量线状符号填充算法研究[J].地理与地理信息科学,2004(7):12~14
The Research of Mathematical Definition of Line Symbols and Its Application
Yang Tao1,2,Zhang JianFeng2
(1.School of Mathematics,Physics&Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China;2.Lanzhou Institute of Survey and Investigation,Lanzhou 730030,China)
There are three topological mappings of f,g,q relation between mapping object x and map symbol qgf(x). On this basis,this paper analyses the characteristic of linear map symbol,gives the mathematical definition of semi-scale linear symbol,and describes the mathematical foundations of meta-data’s rotation,deformation and clipping to construct linear vector symbol.In the end,it is realized through object-oriented programming method and the experiment results show that it works well and has higher drawing quality.
cartographic symbol;linear symbol;mathematical definition;object-oriented
1672-8262(2011)02-53-04
P312
B
2010—07—28
杨涛(1984—),男,硕士研究生,研究方向:GIS方面的研究和开发。
