沙粒蠕移运动速度测量及其统计分析

张 洋,王 元,王 丽

(西安交通大学流体机械及工程系,西安 710049)

0 引 言

风沙流中沙粒在外力作用下沿地表的滚动和滑动称为蠕移,作为风吹沙粒的三种基本运动方式之一,它在风沙动力学研究中有着举足轻重的作用[1]。一方面,蠕移是沙床中较大颗粒的主要运动方式;另一方面,蠕移是床面构型变化的主要原因：由于蠕移和跃移粒径及速度的差异,沙床粒配会随风沙迁移发生变化,沙粒的堆积和输移交替发生,最终导致沙波纹等床面构型的发展。

由于测量上的困难,目前研究沙粒蠕移的文献较少,已有的工作也仅以床面构型模拟及输沙率推算为主。Werner[2]应用离散元法(DEM)、王光谦等[3]通过给定蠕移动量交换规则模拟床面沙波纹;郑晓静等运用粒子流动模型对沙粒蠕移流量进行预测,并提出离散粒子追踪法(DPTM)来确定蠕移沙粒终止位置[4-5], Dong等[6]通过风洞实验中输沙率随高度分布曲线来反推蠕移平均输沙率。这些工作都需要更为精细的实验支持。在高速光学测量的基础上[7]发展了系统性的沙粒蠕移轨迹计算方法,并对两种按起动方式划分的蠕移运动速度进行了统计分析。

1 蠕移运动的高速光学测量

实验在西安交通大学流体工程系的大气边界层(ABL)风洞中进行[7],实验段尺寸为7.4m×0.6m× 0.5m。采用PCO-1200hs高速相机以俯视角拍摄蠕移运动,图像分辨率1280pixel×1024pixel,采集频率500Hz。如图1,采取两项措施：(1)环绕风洞壁放置高亮度卤素灯(1kW)形成无影体照明系统,最大程度消除跃移运动颗粒在床面上的投影影响;(2)相机前加装具备大光圈的长焦镜头,并在镜头与相机间加置数量可变的延伸环来尽可能地缩短工作距离。上述措施将拍摄景深控制在理想范围之内,从而使蠕移层之上的运动颗粒无法被聚焦拍摄,保证了采集对象的单一性。

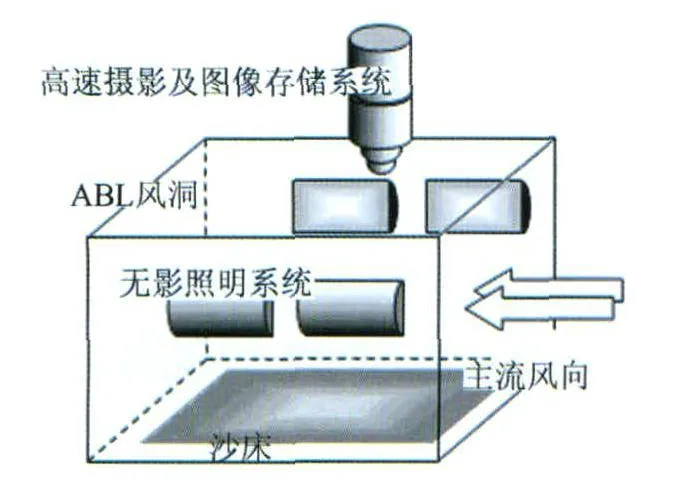
图1 蠕移实验平台Fig.1 Sketch of experiment system

实验采用8组沙样：＜100μ m,100～125μ m, 125～200μ m,200～250μ m,250～400μ m,400～500μ m,500～800μ m,800～1000μ m。对每个工况重复三次试验,每次试验采集一个由3000个连续瞬时组成的图像序列;所提取的蠕移轨迹总数量均在4000条以上,且统计计算包含所有这些轨迹,统计分析的可靠性得到保障。如3.1所述,统计分析蠕移速度分布中的“双峰现象”在前4组结果中较好地复现,但在后4组中因粒径较大、跃移运动十分微弱而不明显,原因见3.1;而且受篇幅限制,3.1中的讨论仅以第二组100～125μ m为例。

2 图像处理及蠕移轨迹提取

2.1 颗粒识别

床面蠕移灰度图像如图2(a)所示。帧间颗粒匹配是获取蠕移轨迹和单颗粒速度的前提,相对于计算微区域平均欧拉速度的传统PIV算法,拉格朗日假设下的PTV(particle tracking velocimetry,粒子追踪测速)算法无疑更为合适。为达到PTV的计算前提,需提取单像素化的蠕移颗粒。首先,运用非负图像减法[7]去除不动颗粒组成的图像背景：

其中,Ai-1、Ai、Ai+1分别代表i-1、i、i+1瞬时的灰度矩阵,S()代表非负算子。由于非负图像减法的中心差分格式,图像序列首尾两张不作运算;得到的仅包含运动沙粒及图像噪点。然后利用自动阈值法[8]较为准确地实现粒子单像素化及图像噪点的消除,见图2(b)。

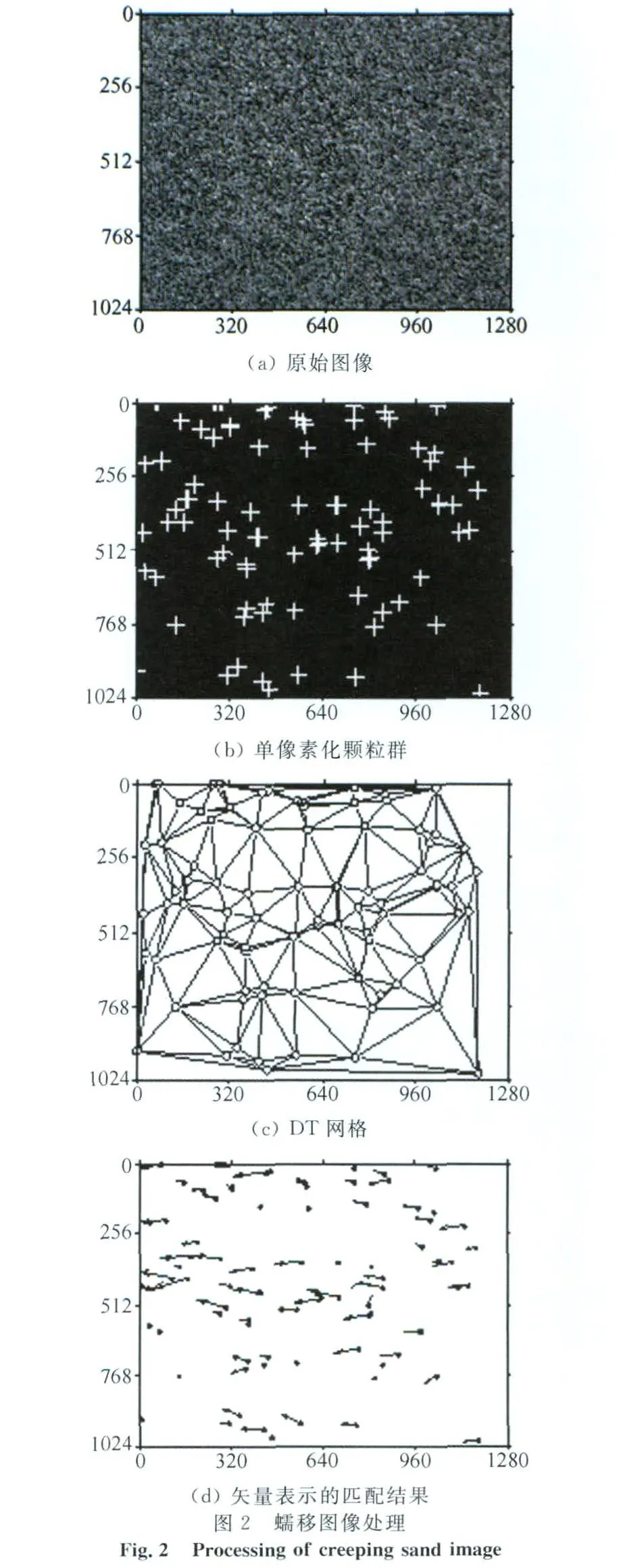
2.2 颗粒匹配及轨迹提取

在获取单像素化粒子群位置坐标的基础上,运用双向DT-PTV算法[9](Bidirectional Delaunay Tes-sellation-based PTV,基于三角分割的双向PTV)进行帧间粒子匹配,粒子群Delaunay网格以及用矢量显示的匹配结果分别见图2(c)、(d)(图2数字坐标的单位为pixel)。一方面,从假设的简洁性、运算速度、准确率及处理对象为离散相等多角度看,DTPTV优于一些经典PTV算法[10](诸如文献[7]所采用的BICC-PTV);另一方面,经过“双向算法”升级的DT-PTV与其单向算法相比具备更高的准确率[9]。故经过非负图像减法、自动阈值法以及双向DTPTV的依次运算,可得到较为准确的帧间匹配关系。蠕移轨迹从连续帧匹配关系中提取。图3显示摩阻风速U＊=0.7m/s下第三组沙在采集时间T=6s内的部分蠕移轨迹。

图3 蠕移轨迹Fig.3 Trajectories of creeping sand

3 实验结果及分析

3.1 蠕移速度分布

一条步长为nT的轨迹可通过差分方法提取nT -1个速度[11]。这些速度均为蠕移速度v,轨迹第一步和最后一步的速度分别称为蠕移起动速度v1和蠕移终止速度v2。蠕移运动具备一个特性：①不同于跃移轨迹的明显加速过程,蠕移运动轨迹速度变化较小(最后时刻骤停)。若一条轨迹满足0.8≤|v2/v1|≤1.2,则称其历程稳定;历程稳定的轨迹数量与轨迹总数量的比值称为轨迹稳定率ηV。以第二组沙(100～125μ m)为例,所有摩阻风速U＊对应的ηV值均不低于88%,如图4所示。设某一工况下所有轨迹v和v1的绝对值的集合分别为V和V1,显然V1⊂V。这样处理的目的在于将速度值与轨迹步长综合考虑从而避免给统计分析带来偏差。对全体沙样进行V和V1的统计分析,发现其分布均存在双峰现象,见图5。如1节所述,以第二组沙为例。

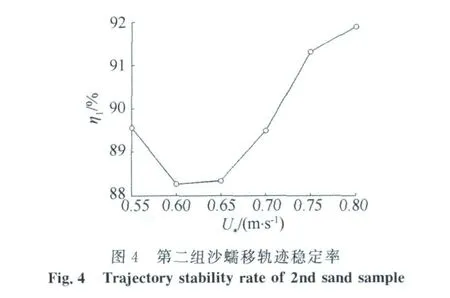
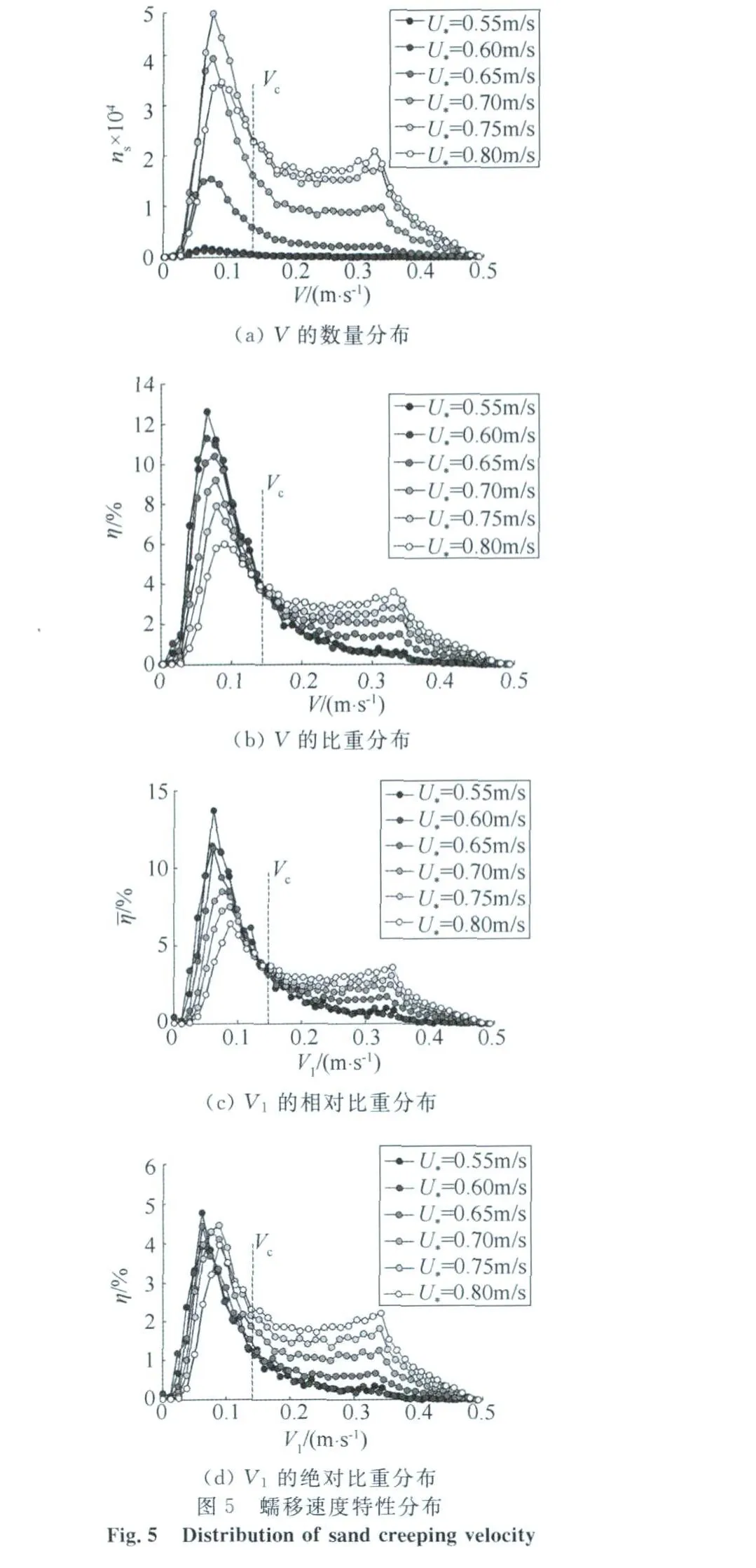
图5(a)为V的数量分布。ns是速度为V的颗粒的数量。分布中的双峰实际上代表按起动方式划分的两种蠕移颗粒：风吹起动颗粒和碰撞起动颗粒(以m1、m2表示),它们分别指在流体作用下沿床面的滚动,以及在颗粒(以跃移为主)的高速碰撞下摆脱静止状态、但因能量或起动角不足以跃移而只能沿床表面运动。一般地,m2的速度大于m1速度。如图5 (a),随着U＊上升,沙床获得的能量增大且跃移运动规模增大,故m1、m2数量均开始增大;当U＊超过一定阈值后,越来越多的颗粒将获得较大能量并以跃移方式脱离地面,m1数量开始降低。由于蠕移的运动特性①,V1与V的数量分布类似。由图5得到蠕移的另一个运动特性：②特征粒径确定的蠕移颗粒速度范围变化极小,受摩阻风速影响甚微。

图5(b)表示V的比重分布,η是速度为V的瞬时颗粒在全体瞬时颗粒中所占比重;5(c)表示V1的相对比重分布,¯η是速度为V1的起动颗粒在全体起动颗粒中所占比重;二者的相似性从另一侧面反映出蠕移运动的特性①。在①②的前提下,可通过临界速度VC将V(或V1)划为分别代表m1、m2的速度Vm1和(或)的计算方法可简述为：相同统计区间下各摩阻风速对应的比重值所组成的数列具有一个表征大小顺序的度数,则存在唯一的VC将全体数列分为两个顺序度相反的部分。图5(d)表示蠕移起动速度V1的绝对比重分布,η在此表示速度为的起动颗粒在全体瞬时颗粒中所占比重。可以看出,随着U＊上升,比重基本稳定,而比重上升,这意味着非起动速度总比重的整体下降。

3.2 蠕移运动比重随U＊的变化

在得到VC之后,可进一步定义若干代表m1和m2在整体运动中所占比重的量,从而分析两种运动方式的权重随摩阻风速变化的规律：

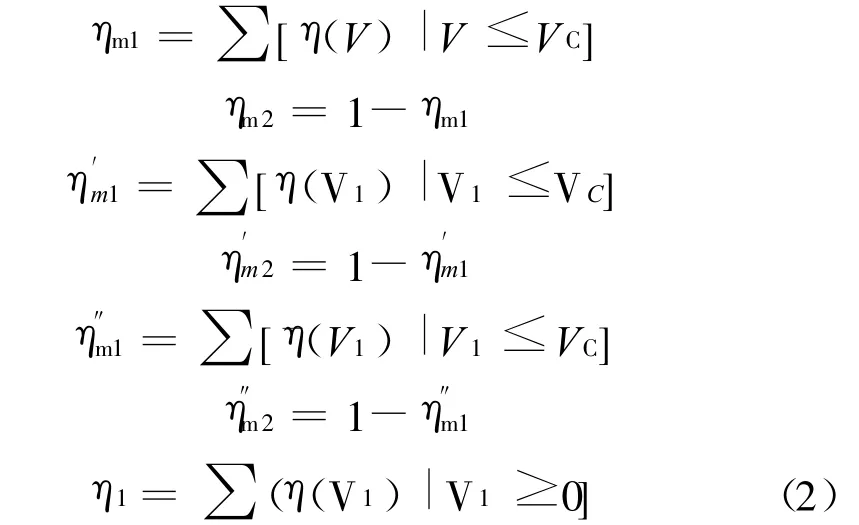
ηm1和ηm2分别代表两种蠕移运动在整体蠕移运动中的比重,η′m1和η′m2分别代表两种蠕移起动方式在整体蠕移运动中的比重,η″m1和η″m2分别代表全体“起动”中两种起动方式的比重;η1代表“起动”在全体瞬时运动中的比重。

如图6(a)、(b)所示,由于蠕移运动的特性①,随着U＊增加,ηm1和和的变化趋势分别相似。如3.1所述,随着U＊增加,起动条件占优的颗粒(如大的迎风面积)将越倾向于以跃移方式起动,而其余的颗粒将在规模增大的跃移颗粒的碰撞下开始蠕移。数值相对稳定,表明了风吹蠕移运动在达到临界之前是蠕移运动中的稳定变化部分,而的趋势则表明碰撞蠕移运动是蠕移运动中的动态变化部分。

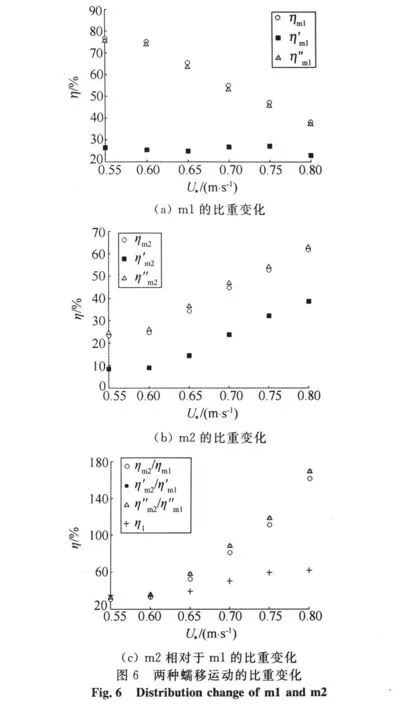
如图6(c),无论是在全体起动还是整体运动中,在U＊达到一个临界摩阻风速之后m2相对于m1的比重开始大于1,这意味着运动形式主导地位的转移。另外,起动的总比重η1随U＊增加而增加;这是因为m2代表着跃移入射的高随机性,其比重增加导致沙床表面运动随机性增强,即单沙粒的实际轨迹更易呈断续状的n个分段,在采集频率较高的前提下则对应为n条步长较短的数字轨迹;因此非起动速度的整体数量和比重下降。m2的比重可作为床面随机性的量化标识之一。

4 结 论

(1)蠕移运动图像是连续型无影照明系统下的俯视拍摄结果,存在不动颗粒组成的背景。而非负图像减法、自动阈值法及双向粒子追踪算法的有机结合能够很好地从此类图像中提取有效的颗粒轨迹;

(2)蠕移总速度及起动速度的统计结果表明,当近床面同时存在跃移和蠕移运动时,流体起动蠕移代表整个运动的稳定变化部分,其比重随摩阻风速增大而减小;碰撞起动蠕移则代表动态变化部分,其比重随摩阻风速增大而增大。在摩阻风速超过临界值之后,蠕移起动的主导形式将从流体起动转化为碰撞起动;

(3)两种蠕移运动的相对比重变化与沙样特征粒径以及跃移运动关系密切。因此发展蠕、跃同时测量技术将是研究床面运动形式相互作用及转化的重要突破口。

[1] ANDERSON R S,BUNAS K L.Grain size segregation and stratigraphy in aeloian ripples modelled with a cellular automaton[J].Nature,1993,365(2)：740-743.

[2] WERNER B T.A physical model of wind-blown sand transport[D].California,US：California Institute of Technology,1987.

[3] 王光谦,冉启华,刘绿波.风成沙纹过程的计算机模拟[J].泥沙研究,1998(3)：1-6.

[4] WANG Z T,ZHENG X J.Heoretical prediction of creep flux in aeolian sand transport[J].Powder Technology, 2004,139(2)：123-128.

[5] 郑晓静,薄天利,谢 莉.风成沙波纹的离散粒子追踪法模拟[J].中国科学G,2007,37(4)：527-534.

[6] DONG Z B,LIU X P,WANG H T,et al.The flux profile of a blowing sand cloud：a wind tunnel investigation [J].Geomorphology,2002,49(3-4)：219-230.

[7] WANG Y,WANG D W,WANG L,et al.Measurement of sand creep on a flat sand bed using a high-speed digital camera[J].Sedimentology,2009,56(6)：1705-1712.

[8] OHMI K,LI H Y.Particle-tracking velocimetry with new algorithms[J].M eas.Sci.Technol.,2000,11 (6)：603-616.

[9] 张 洋,王 元,王大伟.DT-PTV离散相伪矢量的概率择优式剔除算法[J].西安交通大学学报,2009,43 (5)：119-123.

[10]SONG X Q,YAMAMOTO F,IGUCHI M,et al.A new tracking algorithm of PIV and removal of spurious vectors using Delaunay tessellation[J].Exp.Fluids, 1999,26(4)：371-380.

[11]ZHANG W,KANG J H,LEE S J.Tracking of saltating sand trajectories over a flat surface embedded in an atmospheric boundary layer[J].Geomorphology,2007, 86(3)：320-331.