一种基于灰色模型的预测调度算法

陈鑫杰

(福建八达电信技术有限公司，福建漳州363108)

1.引言

无线传感器网络(Wireless Sensor Networks，WSNs)是一种具有广泛用途的网络。在应用环境中布置传感器节点时，为了保证监控的质量，通常需要密集地部署节点。当网络中的所有节点都处于工作状态时，一旦检测到某个事件发生，多个节点都会捕捉到信息向上提交，从而引起无线信道的冲突与感知数据的重传，不仅增加了通信的时延，降低了网络的吞吐量，也浪费了节点的能量，缩短了网络的生存时间。解决这一问题的有效办法就是对节点的状态进行调度，让节点轮流工作和休眠，以减少信息的发送和信道的冲突。

目前科研人员已经提出了许多调度算法。在节点分布满足泊松静态点过程条件下，Hisn[1]等把节点调度分为两种：节点随机调度和节点协作调度。节点随机调度算法[2-3]仅执行一次，通过随机分组形式将每个传感器节点划分到某一组或某几组，算法结束之后，依次调度每一组的节点工作。节点协作调度算法需要节点与周围节点进行通信，且传感器节点在每一轮的开始执行一次算法，按照某种竞争机制从所有节点中选择若干个节点作为活动节点。节点协作调度算法又可以进一步分为基于位置信息的节点调度[4]和无位置信息的节点调度[5]。可以看出，节点调度问题与覆盖性能、路由规划和网络连通性等问题存在一定关联。

与上述研究的思路不同，本文利用节点采集数据在时间上的相关性，提出了一种基于灰色模型[6]的预测调度算法(PSGM)。PSGM尽量让能量较低的节点休眠，并采用灰色模型来预测节点休眠时丢失的数据。仿真结果表明，算法能够有效地延长网络的生命周期，达到了设计的目标。

2.网络模型

PSGM算法对WSNs做如下假设：

(1)节点：所有的节点同质，初始能量相同，并具有数据缓存能力。sink节点除了具有较高的能量外，其它设置与一般节点相同。

(2)分布：节点被随机布置在一个矩形区域内，并假定每个节点可以获取自己的能量信息。

(3)网络结构：网络为一个两层的簇结构。节点可以按多种方法分簇，如位置相关、应用设定、随机产生等，簇中成员产生数据后向簇头节点发送，簇头节点汇总所有簇成员的数据后，合并成一个数据包发送给sink节点。

3.灰色模型

灰色预测法是一种对含有不确定因素的系统进行预测的方法。自灰色系统理论问世以来，灰色预测的理论与应用研究都取得了较大的进展。灰色预测控制的显著特点就是在信息不足的情况下获得较好的控制效果。灰色模型有许多种，其中GM(1，1)模型是由邓聚龙教授提出的一个经典灰色预测模型。GM(1，1)模型建模的过程是：首先对原始数据进行累加，得到呈一定规律的新的序列，其相应的曲线或折线可以用典型曲线来逼近，然后用逼近的曲线作为模型，以此来对系统进行预测。具体过程阐述如下。

假设GM(1，1)的原始时间序列有n个观察值，为：X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}。在实际问题中，这一组数据提供的信息并不完全，具有很大的随机性。为了使其呈现一定的规律性，一般对其进行一次累加处理，经过数据处理后的时间序列称为生成列，公式如(1)所示。

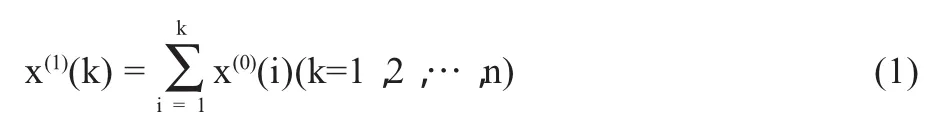
得到新的序列后，运用数学中的动态线性模型对生成的数据进行拟合和逼近，得到微分方程式如(2)所示。

其中，a称为发展系数，u称作内生控制灰数。此时满足的临界条件是x(1)(1)=x(0)(1)。微分方程式中的a和u均为待求解的未知变量。求出a和u的估计值后，将其代入方程式中，得到与时间有关的方程，如(3)所示。

使用式(3)即可进行数据的拟合与预测。

4.基于灰色模型的预测调度算法

PSGM是基于分层拓扑的网络结构。其主要思路是，簇成员向簇首节点发送数据时，顺带发送自己的剩余能量。簇首节点接收到数据后，将其保存。并根据节点的能量状况，选取簇中能量较低的节点，通知其休眠。在下一轮提交数据时，簇首节点根据休眠节点前面提交的数据预测出其应提交的数据。

4.1 数据的预测

PSGM算法的核心步骤就是簇首节点对休眠节点进行的数据预测。为了实现这个功能，PSGM算法采用了GM(1，1)模型。算法的主要步骤是：

首先，簇首节点为每一个簇成员节点k建立一个数组data，用于保存该节点k的前n个数据。这n个数据可以是节点k提交过来的，也可以是节点k休眠时由簇首节点计算出来的。

如果节点在本轮中没有休眠，则簇首节点将其提交的数据放入data中，并剔除最旧的数据。如果节点被调度休眠，则簇首节点取出data数组中的数据，作为X(0)序列，进行累加处理后得到X(1)序列，将其带入(2)中，解出a和u的值后，生成(3)式，并计算出n+1项的值，即作为此轮的预测值。同样的，该预测值也应放入data数组中，并剔除最旧的数据。

n的选择跟具体的应用相关，数据波动较大的环境n值应相应增大，否则可以减小。在我们的试验中，n取值15。

为了防止误差的累积，尽可能提高预测的精度，在PSGM算法中，节点不能连续休眠两轮。即休眠节点即使其能量仍为最低，下一轮也必须工作，这样可以确保序列中至少有50%的真实数据。

4.2 算法流程

PSGM算法的具体步骤如下：

(1)初始化：网络进行初始化分簇工作。分簇算法可以采用已有的算法，也可以人工设定。

(2)获得初始的时间序列：所有的节点先工作n轮，向簇首节点提交n个数据，发送数据时顺带提交自己的剩余能量。簇首节点一方面将收集的数据聚合后提交给sink节点，另一方面保存每个节点的n个数据。

(3)调度休眠：从第n+1轮开始，簇首节点根据簇内成员的能量情况按照一定的比率r来选择节点，通知其休眠。选择节点时，忽略上轮已休眠过的节点。

(4)预测数据：预测节点针对休眠节点进行数据预测，并更新其data数组。然后簇首节点将预测数据与收集的真实数据一起聚合后向上提交。

(5)唤醒节点：休眠节点休息一轮后，进入工作状态。

(6)循环(3)～(5)，直至网络重新分簇或死亡。

5.仿真试验

为了验证算法的性能，本文在NS2仿真平台下实现了PSGM算法，并采用实际收集的温度数据作为测试样本。仿真场景的参数如表1所示。

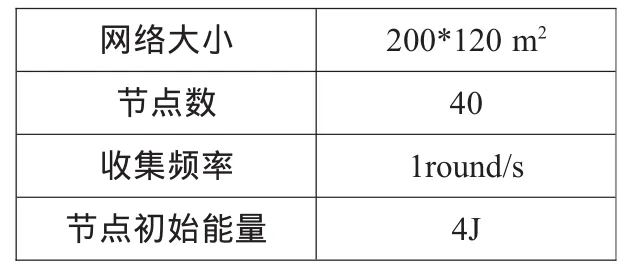
表1 仿真场景的设置

节点的分布如图1所示。为了验证算法的性能，我们主要考察两个指标：网络生命周期和数据误差率。

(1)网络的生命周期：本文将网络中第一个节点死亡的时间定义为网络生命周期。当节点剩余能量低于0.005J时，我们认为该节点已不能工作。

(2)数据误差率：数据误差率是衡量预测算法性能的重要指标。本文的数据误差率定义为所有休眠节点的误差率的平均值。

网络生命周期的测试结果如图2所示。图中横坐标为休眠比率r。r=0时即对应所有节点都工作的情况，由图2可以看出，休眠的节点数越多，网络节约的能耗越多，网络的生命周期也越长。

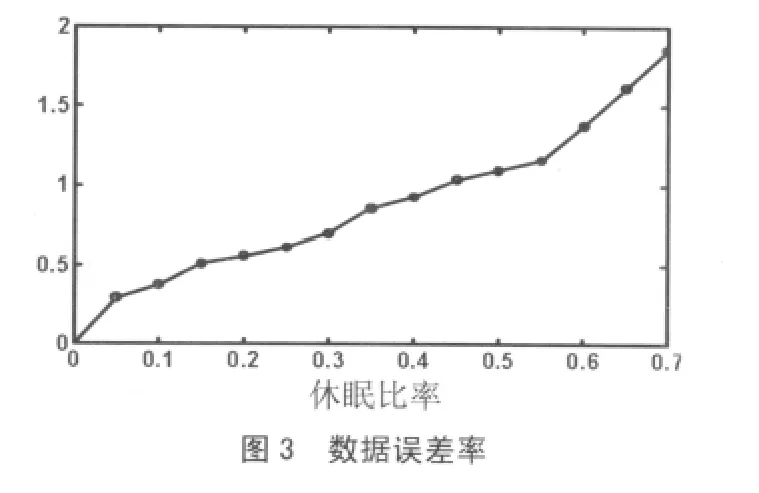
数据误差率的测试结果如图3所示。由图3可以看出，数据的误差随着休眠节点的增多而有所提高，但即使节点休眠率r=0.7时，数据的误差率也不超过2%，效果较好。

6.结束语

本文利用传感数据的相关性，提出了一种基于预测的调度算法PSGM。仿真结果表明，该算法不仅有效地延长了网络生命周期，而且数据的精度也较高，误差控制在可接受的范围内，因而可以在很多应用领域中推广。

[1]Hsin C，Liu M.Network coverage using low duty-cycled sensors：random&coordinated sleep algorithms[C].Proceedings of the Third International Symposium on Information Processing in Sensor Networks(IPSN’04)，ACM，2004，433-442.

[2]Kumar S，Lai T H，Balogh J.On k-coverage in a mostly sleeping sensor networks[C].Proceeding of the 10th annual international conference on Mobile computing and networking，ACM，2004，144-158.

[3]Slijepcevic S，Potkonjak M.Power efficient organization of wireless sensor networks[C].Proceeding of the IEEE International Conference on Communications(ICC’01)，2001，472-476.

[4]Zhang H，Hou J.Maintaining sensing coverage and connectivity in large sensor networks[J].Ad Hoc&Sensor Wireless Networks，2005，1(1-2)：89-124.

[5]Gao Y，Wu K，Li F.Analysis on the redundancy of wireless sensor networks[C].Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications，2003，108-114.

[6]Xue-liang Bi，Tie Yan，Lei Chang，Chang-jiang Wang.Gray Correlation Analysis Method and Its Application in Drill Stem Failure in Oil and Gas Engineering[C].International Conference on Natural Computation，2008，502-505.