中国工业生产的劳动、资本和能源的替代分析

吴力波

(复旦大学能源经济与战略研究中心,上海 200433)

近年来,中国经济增长的可持续性开始遭到国内能源供给存量不足的瓶颈制约和能源价格上涨带来的冲击,能源供给面临的存量与流量的双重约束,因此以节能降耗为重心的能源替代将成为中国经济发展必然的选择。能源替代可以分为内部替代和外部替代。内部替代主要指能源内部的结构以及新兴能源的研发和规模应用,取决于工程技术的开发与应用规模,因而更多地涉及到技术问题。外部替代则强调能源与资本、劳动以及原材料之间的替代,往往需要通过资源的优化配置而达到替代目的,因而呈现更多的经济性特征。

国家产业政策的制定往往受到投入要素之间关系的影响。比如,当能源与资本之间呈现替代关系时,促进能源节约就可以借助于资本投入的增加;反之,当两者没有相关性或者呈现互补关系时,试图扩大资本投入来替代能源投入就会因为能源缺乏需求弹性而达不到预期的效果,此时能源节约更多地依托于纯技术性的工程。由于研究手法和各国经济结构的不同,已有的研究对于各要素之间的互补替代关系无统一的定论。我国有关能源替代的研究目前尚处于起步阶段,针对国内能源与其他要素关系的研究,还存在不确定性和替代性两种不同的观点。本文将用实证的方法考察中国工业生产部门各投入要素之间的替代与互补关系。

1 理论模型与实证框架

1.1 成本函数和要素需求函数

假设中国工业部门的生产函数共有三个投入要素(分别为劳动、资本和能源),并且这一生产函数规模报酬不变,所有影响劳动、资本和能源投入量的技术都是希克斯中性的,存在唯一的成本函数与生产函数一一对应。满足假设的成本函数可以有很多种形式,比如里昂惕夫形式、科布·道格拉斯形式,或者超越对数形式。本文将沿用大部分文献采用的超越对数形式:

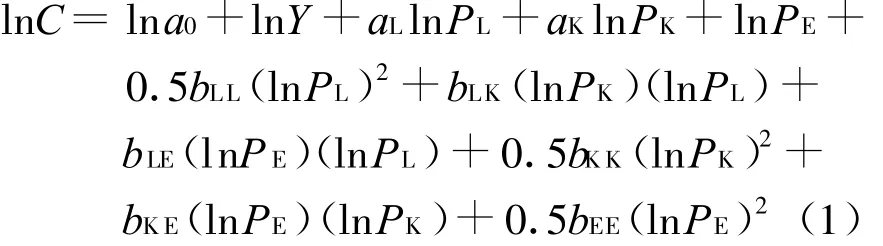
式中:C为成本;a0为系数;aL,aK和aE分别为与劳动、资本和能源项有关的系数;PL,PK和PE分别为劳动、资本和能源的价格;bLK为劳动与资本之间的相关系数;bLE为劳动与能源之间的相关系数。

假设规模报酬不变,成本函数对要素价格一次齐次,从而可以得到4个约束方程:

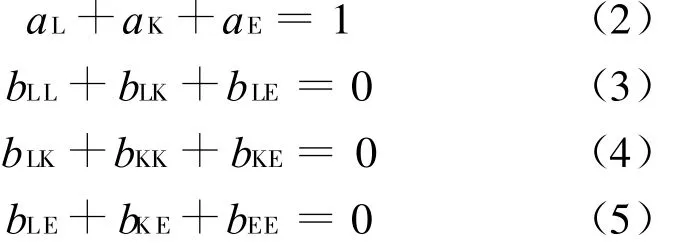
对式(1)ln(Pi)求偏导,结合Shepherd引理(d C/d Pi=Xi),劳动、资本和能源成本占总成本的比例s L,s K和s E为:

根据约束条件(2)和(3),这3个方程之间存在多重共线性,为此留下约束条件(7)和(8)作为估计方程。利用约束条件(4)和(5)可以得到计量回归的计算式:

式中的系数b KK,b KE等可以通过约束方程组计算得到。

1.2 要素替代弹性

1)AES弹性 即A llen局部替代弹性:

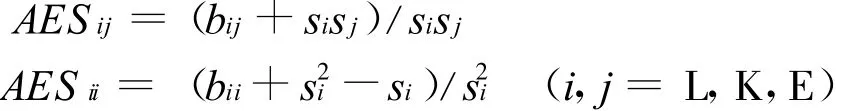
AES存在着许多难以克服的缺陷,Blackorby和Russell指出,由于AES既无法提供两种要素相对比例以及等量曲线形状,也无法通过边际替代率来解释,因此从整体上说,局部替代弹性AES并不能充分解释两种要素之间的替代率。不过尽管AES并非一个描述要素替代弹性的最佳指标,但是因为以下计算交叉价格弹性CPE和相对替代弹性MES的过程中需要用到AES,因此本文还是给出了AES的计算结果。

2)CPE弹性 即交叉价格弹性,反映要素j价格变化所能导致的要素i的绝对量变化:

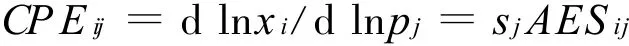
当交叉价格弹性CPE的值大于0时,要素i与要素j为CPE替代关系;当CPE的值小于时,要素i与要素j为CPE互补关系。

CPE无法对两种要素之间的相对替代率(要素投入比例的变化对价格变化的反应程度)给出明确的解释。举例来说,即使能源与劳动之间存在绝对互补关系,能源价格上升导致了劳动总量需求的减少,但单位投入的劳动数量相对于能源数量仍然可能存在上升的现象。这是因为当能源价格提高时,受技术等外在因素限制,微观单位内的劳动能源投入比例在短期内难以调整,能源需求减少有可能导致单位劳动需求的减少。但是在宏观层面,能源价格的上升将使社会需求偏向劳动或资本密集型的产品,结果能源密集型产业的产出下降,导致能源投入的减少,并超过了劳动力需求的减少,这样能源与劳动之间就呈现出替代关系。

3)MES弹性 即相对替代弹性,表示要素j价格变化导致的要素i(相对要素j)使用量的变化。1967年M orishima提出MES并用力估计两种投入要素比例变化对价格变化的反应程度, 1981年Blackorby和 Russell发展了Morishima的理论,通过对双重成本函数的扩展,并运用Shepherd引理实现了 Hicks边际替代率和两种以上投入要素替代率的整合。MES的算式为:

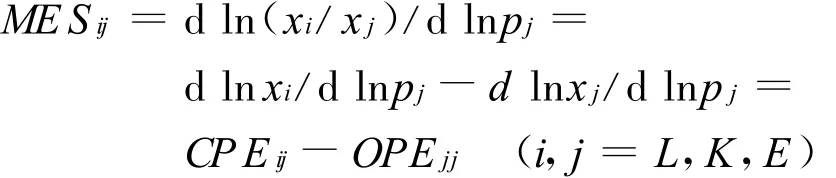
式中:pj为要素j的价格;CPEij为要素i和j之间的交叉价格弹性;OPEjj为要素j的自价格需求弹性,一般的正常物品,OPE的值小于0。

当相对替代弹性MES的值大于0时,要素i与要素j为MES替代关系;当MES的值小于0时,要素i与要素j为M ES互补关系。

2 实证分析的数据收集

为了估计式(9)和式(10)需要得到三种要素的成本占比和价格序列。本文的实证分析采用1986年—2006年间的年度数据,如不加特别说明均来源于国家统计局网站电子年鉴。

2.1 劳动价格和总成本

比较理想的劳动价格指数应该由工业部门的平均工资指数所表征,但由于缺少历年来工业部门的就业和工资统计资料,因此无法对各部门的平均工资进行加权。不过工业部门的就业人数占全社会就业人数的比例较高,因此可以用职工平均工资代表工业部门的平均工资,用职工实际平均工资价格指数代表工业部门的劳动价格指数。工业部门的劳动存量由第二产业就业总人数代表。因此,劳动总成本等于职工平均工资乘以第二产业就业总人数。

2.2 资本价格和总成本

资本总成本与资本价格和固定资本原价成正比。本文采用Romer公式测算资本使用价格:

式中:r(t)为名义利率,取我国一年至三年期(含三年)贷款利率(一年期利率和三年期利率的利差为2%);d为折旧率,按15年折旧期限计算为6.7%左右;t为边际所得公司税率;π(t)为资本真实价格变化率。

由于边际所得公司税率的统计困难,并且对于资本价格的影响又十分有限,因此可以认为t =0。由此可以得到:

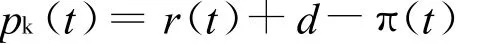
关于中国资本存量估算的研究很多,目前许多国内学者都采用永续盘存法来估计我国的资本存量K:

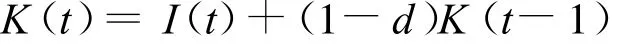
式中:I为当年投资流量。

利用该方法计算得到的资本存量对于折旧率太敏感,特别是我国折旧率目前尚无统一标准,很可能产生较大误差,而且样本区间越大误差也越大。因此本文将使用固定资产原价作为资本存量的近似。由于折旧的存在,用固定资产原价来表征资本存量存在高估的可能,但这一误差是可控的,不会像永续盘存法那样积累到下一年。

2.3 能源价格和总成本

由于对于各能源品种的价格缺少口径统一的统计,本文将采用燃料动力价格指数作为能源要素的价格指数。工业部门能源总成本与能源使用总量和能源平均加权价格有关。为了得到能源平均加权价格就必须确定某个基准年的能源价格水平,然后结合燃料动力价格指数得到各年份的价格水平,本文选取2006年为基准年。工业部门使用的能源品种包括煤炭、原油、汽油、柴油、燃料油、天然气和电力,其中电力价格数据为各地区加权零售电价,由2008中国电力行业年度发展报告得到,其余价格数据均从国际能源署(IEA)数据库得到。

2.4 三大要素的价格指数和成本占比的变化

根据以上计算方法得到的劳动、资本和能源三大要素价格指数和成本占比以及价格指数的变化见图1和图2。

图11986 年—2006年工业部门三大要素成本占比变化

图21986 年—2006年工业部门三大要素价格指数变化

从图1中可以看到,中国劳动密集型增长的特征非常明显,在总要素成本中劳动成本一直以来都占据了半壁江山。从图1中还可以看到,与资本相比,能源的总成本比例更大,其中资本在1994年前后的成本占比有异常小的值;这主要是因为当年的实际利率(名义利率减去通胀)非常小。由于2002年之后工业部门面临“十一五”节能降耗目标的约束,加之市场化进程的深化导致的能源价格从过去过低的价格向市场价格的回归,能源使用成本比例在20世纪末呈现一个明显的下降趋势,并在本世纪维持在30%附近。

从图2可以看到,劳动价格是这三种要素中上涨最快的,能源价格其次,资本价格则一直处于波动状态。资本与能源的价格之所以没有上涨这么快,可能与中国的价格管制还是有一定的关系。在资本市场上,金融压制问题还是比较突出,加之金融市场本身的波动性,导致资本价格也波动较大;在能源市场上,各种价格管制(如成品油价格管制等)在中国十分普遍,使得能源价格无法根据市场供求关系自由调整,上升速度相对较为缓慢。

3 实证结果与分析

3.1 参数估计结果

结合约束方程,用联立方程组的方法对式(9)和式(10)进行估计,得到的参数估计结果见表1。

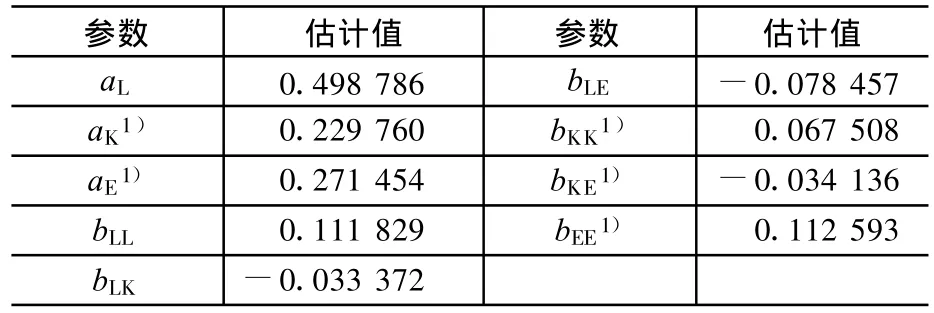
表1 参数估计

根据以上参数估计结果,套用理论框架部分的公式可计算得到AES,CPE和M ES的值。

3.2 劳动、资本和能源要素的自价格弹性(OPE)分析

1986年—2006年工业部门三大要素自价格弹性的计算结果见图3。计算表明,劳动、资本和能源的自价格弹性均为负数,这符合一般经济学原理,即在三种要素均为正常商品的情况下,一种要素价格的上升将导致其使用量的下降。

比较三种要素的自价格弹性情况可以发现:资本的自价格弹性最高,波动也最大;劳动和能源的自价格弹性较小,波动也较平稳。劳动的自价格弹性较小可能与中国劳动力市场的黏性有关(比如企业不能随意解雇劳动力,以及中国存在比较严重的隐性失业问题),这种弹性在最近几年中逐渐增加,体现了中国劳动力逐渐走向市场化的成效。

图31986 年—2006年工业部门三大要素自价格弹性

影响能源自价格弹性的因素有两个方面:一方面,能源市场化的步伐和国家“节能降耗”硬约束的存在,使能源自价格弹性趋于上升;另一方面,中国高度依赖重工业等高耗能产业的经济发展模式,又对能源自价格弹性上升的趋势起到消融作用。从图3中可以看到,能源自价格弹性总体处于一个较低的水平,这说明对于能源的需求总体具有较大的刚性,而从20世纪90年代中期到20世纪末缓慢下降的能源自价格弹性同样表明,与能源市场化进程等倾向于提高能源自价格弹性的因素相比,中国对高耗能产业的依赖还是在这一时期起到了主导作用。然而进入新千年之后,能源自价格弹性逐渐上升,这或许是中国经济发展转型成效的初显。资本的自价格弹性高于劳动和能源的自价格弹性,说明相对劳动和能源要素以及厂商使用资本对于价格更为敏感。资本自价格弹性在后期稍高于前期,可以认为我国金融市场的逐渐完善,资本使用已经能反映价格因素;劳动和能源的自价格弹性比较接近,但与能源相比,企业对于劳动力的需求似乎更加缺乏弹性。

3.3 要素交叉价格弹性(CPE)与相对替代弹性(MES)分析

资本—能源和劳动—能源的绝对和相对替代弹性反映了能源与资本、劳动之间均呈现相互替代关系,见图4。可以看到资本—能源替代弹性的时间序列和劳动—能源替代弹性高度一致,劳动使用量对能源价格的敏感性要略微高于资本使用量对能源价格的敏感性。这个结果与美国Woods等人1975年的研究结果能源与资本是互补的关系不同,Putti模型的研究者认为,能源与资本的互补关系主要是源于机器要使用到大量的能源作为其原料,而本文的研究结果表明,中国的资本要素对能源依赖性可能不如一些西方发达国家那么强。

图4 资本—能源和劳动—能源的绝对和相对替代弹性

从CPE上看,尽管资本和劳动与能源之间均存在替代关系,但这种替代效应在绝对量上并不明显,能源价格每上升1%,资本和劳动的使用量平均仅上升0.1%左右。然而从MES上看,与其他两大要素相比,能源价格的上升使能源的使用比例下降的效果更明显,也就是说相对替代弹性的效应更大,因此可以认为,继续逐步放开能源价格使能源价格能够按照市场供求进一步上浮,应该是降低经济结构中能源消耗的一条可行路径。

图5是能源—资本和能源—劳动的绝对和相对替代弹性的计算结果。根据图5可以进一步考察劳动或资本的价格变化对能源使用量可能的影响。

从图5中可以看出,能源使用量的变化对资本和劳动力价格缺乏弹性,表现为CPE的值都小于1。但与能源对资本价格的关系相比,能源对劳动价格影响更为敏感;两者的CPE平均值分别在0.1和0.2左右,即资本价格下降1%能源使用量下降不到0.1%,而劳动价格下降1%可以使能源使用量下降超过0.2%。

图5 能源—资本和能源—劳动的绝对和相对替代弹性

根据图5中的相对替代弹性MES的变化,可以看到相对替代的效应要比绝对替代更为明显,即劳动或资本价格的下降会导致能源使用比例下降,而且与劳动价格变化对能源使用比例的影响相比,资本价格变化对能源使用比例的影响不确定性更大,主要体现在能源—劳动相对弹性(MESec)剧烈的波动性。由此得出结论,尽管下降幅度相当有限,资本或劳动价格的下降将会导致能源使用比例的下降,并且能源对劳动的替代程度要高于能源对资本的替代程度。