考虑电压稳定约束的电力系统无功规划

程浩忠,顾颖中,熊 宁

(上海交通大学电气工程系,上海 200240)

1 引言

无功规划与传统的无功优化不同。无功优化RPO(Reactive Pow erOptim ization)是在系统现有的无功补偿元件及调节设备范围内,在满足系统各项约束条件下,使系统运行费用(通常是使网络损耗)最小。而无功规划RPP(Reactive Pow er Programming)是为达到某种目标(通常是使系统静态电压稳定裕度高于某个阀值)而对需投入无功备用设备进行规划的问题。

常规无功规划问题的求解方法,主要有试验误差法、非线性规划法、动态规划法、智能进化算法以及线性规划法[1,2]。其中,内点法以其计算效率的高效性和对约束处理的方便性得到了广泛的应用。Karm arkar在1984年提出内点法后[3],许多学者对其进行了扩展研究,相继提出了一些完善方法,并在电力系统中得到了广泛地应用,如将对数壁垒函数与牛顿法结合起来应用到非线性规划问题[4,5]中等。在内点法的基础上,M ehrotra提出了基于预测校正的原对偶内点法[6],由于该方法在计算中引入预测、校正环节,故可以计及互补松弛条件的二次性和动态地确定向心参数的取值,从而能够较好地协调解的最优性及可行性之间的关系,改善算法的收敛性能。

2 负荷裕度指标的定义

负荷裕度指标是评估电力系统静态电压稳定性的有效手段之一。它是指从系统当前运行点到电压崩溃点的“负荷距离”,具有较好的线性和直观性。它可以使运行人员清晰地了解系统目前所处的状态,并提前采取有效措施避免电压崩溃的发生。

如图1所示的P-U曲线,当前系统的运行点是PL0,即表示当前系统的负荷。Pcr对应着系统电压崩溃的临界点,即代表系统所能承受的极限负荷量。Pcr-PL0即为该系统的静态电压稳定负荷裕度。由此可以定义系统的相对负荷裕度λ为:

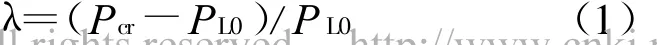
由P-U曲线可以看出,当系统的负荷裕度较大时,系统的电压水平也较高;同样,当系统接近电压崩溃临界点时,系统裕度很小,系统电压水平也相应下降。利用此电压稳定评价指标,可以清晰地表示出系统电压的稳定水平。

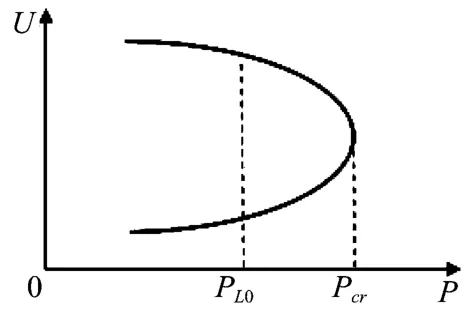
图1 P-U曲线

3 无功规划模型

以新增无功容量总和最小作为目标函数,无功规划模型可用式(2)表示:

(1)等式约束方程h(x)

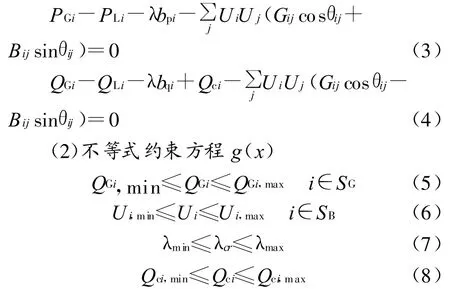
式中:Ui——节点 i的电压幅值;θi——节点 i的相角; Bij——节点i与节点 j之间的互电纳;Gij——节点 i与 j之间的互电导;Qc——补偿容量;λcr——临界点的负荷增量;Qci——节点i补偿无功功率的容量;SB——所有节点的集合;bp——有功负荷增长方向;bq——无功负荷增长方向;SG——无功源集合;PGi——第i个节点发电机的有功;QGi——第i个节点发电机的无功;PLi——第i个节点负荷的有功;QLi——第i个节点负荷的无功;Qci——第i个节点的无功补偿量。

4 模型的求解

采用预测-校正内点法对模型式(2)至式(8)进行求解,构造其拉格朗日函数,如式(9):

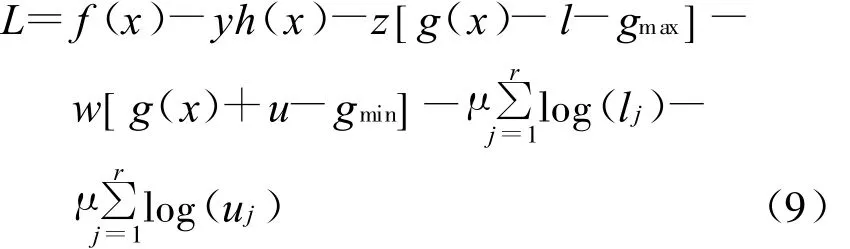
式(9)中,变量μ＞0为扰动因子(或称障碍常数);l,u为松弛变量,且u＞0。

应用牛顿法得到待求问题的修正方程为:

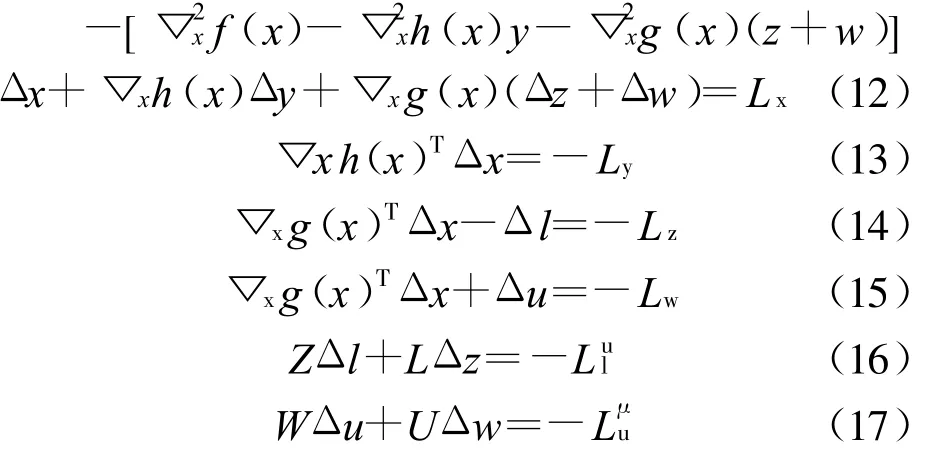
将式(12)至式(17)简化后写成矩阵,如式(18):

只需求解式(18)矩阵右下角分块中的函数值,然后逐一回代,即可求出所有变量。求解方程组如式(19):

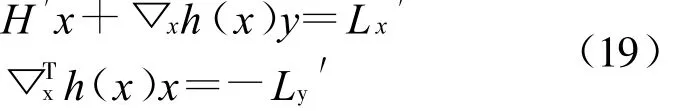
将所得解Δx,Δy回代到式(20),即可求出所有变量的解:

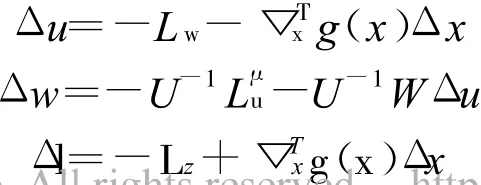
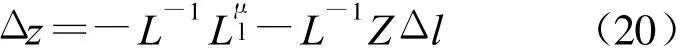
变量更新的迭代方程组为:

式中αd,αp分别为步长:

引入预测及校正环节动态确定向心参数的取值,并且利用互补松弛条件的二次性,预估计算结果,以较好地协调解的最优性及可行性之间的关系,改善算法的收敛性能。

(1)预测环节 对式(12)至式(17)的修正方程,取 μ=0,可求得 ΔxAff,ΔyAff,ΔzAff,ΔlAff, ΔuAff,ΔwAff。

式中:Aff表示仿射方向,即扰动因子取0时的牛顿方向。

根据预测过程,可确定仿射方向下的修正步长,如式(28)及相应的对偶间隙如式(29):

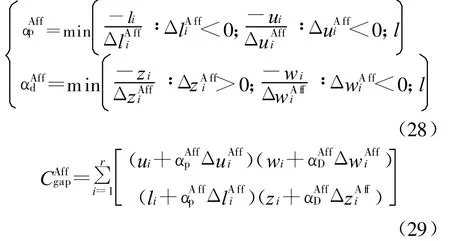
预测-校正原对偶内点法根据当前点的对偶间隙与仿射方向下的对偶间隙间的关系动态给定向心参数值,根据Mehrotra的经验[6],σ一般为:

(2)校正环节 考虑到互补松弛条件式(16)及式(17)的二次性,将二次泰勒方程式展开,可表示为:

将 ΔZAff、ΔlAff、ΔWAff、ΔuAff分别代入,对ΔZΔl及ΔWΔu进行近似,对互补松弛条件进行校正,即:

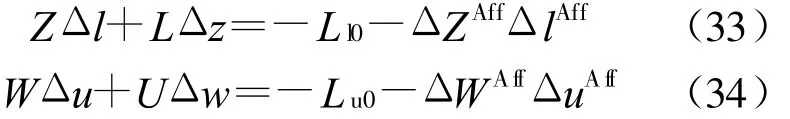
预测-校正原对偶内点法引入了预测-校正机制,充分利用了互补松弛条件的二次性,避开了向心参数的人为选取,同时也提高了收敛性。

5 IEEE标准算例仿真分析与应用

将无功规划模型和求解方法用于IEEE 14、30、57、118标准算例,求解各系统初始负荷裕度结果如表1所示。其中,负荷增长方式设定为根据初始负荷大小全网同比例增长;发电机出力方式设定为系统中所有发电机(平衡机除外)根据各自有功备用的大小按比例分摊负荷的增量;优化目标为将系统原有的负荷裕度提升10%。

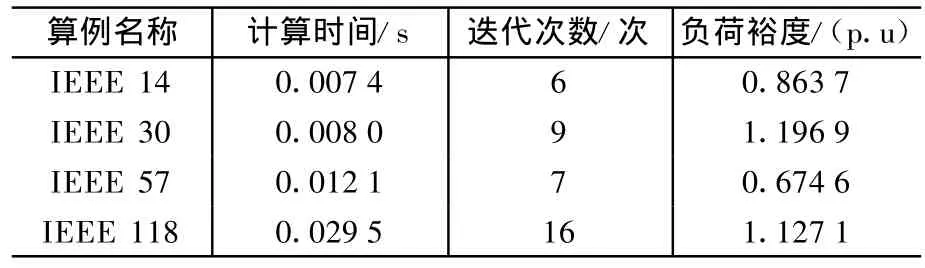
表1 IEEE标准算例负荷裕度求解结果

(1)IEEE 14节点无功补偿方案为:10号节点的无功补偿量为4.57 MW,13号节点的无功补偿量为0.33 MW,14号节点的无功补偿量为11.53MW,总计为16.43 MW。

(2)IEEE 30节点无功补偿方案为:24号节点的无功补偿量为3.85 MW,26号节点的无功补偿量为4.22 MW,29号节点的无功补偿量为1.01 MW,30号节点的无功补偿量为6.28 MW,总计为15.36MW。

(3)IEEE 57节点无功补偿方案为:30号的节点补偿量为4.35 MW,33号节点补偿量为2.91 MW,31号节点补偿量为5.75 MW,总计为13.01MW。

(4)IEEE 118节点无功补偿方案为:1号的节点补偿量为28.28 MW,9号的节点补偿量为86.67MW,总计为114.93MW。

上述无功补偿量计算中所需时间随节点数量的增多而线性增大,但是其增加的速率基本是多项式级的,由此证明内点法适合解算大规模系统问题。

利用上述无功规划模型,在国内某个大型电力系统上验证所提方法的有效性。负荷增长方式和发电机出力方式与上述定义相同,补偿候选点集合为220 kV主变的低压侧节点,各节点无功补偿下限为0,上限为主变容量的20%。

采用预测-校正原对偶内点法对该电网进行无功规划,补偿方案如表2所示。

如表2所示,该系统共有38个节点需要安装无功补偿设备,补偿容量总计为354.05 MW。

表2 国内某系统无功补偿方案 MW

算法收敛过程如图2所示。

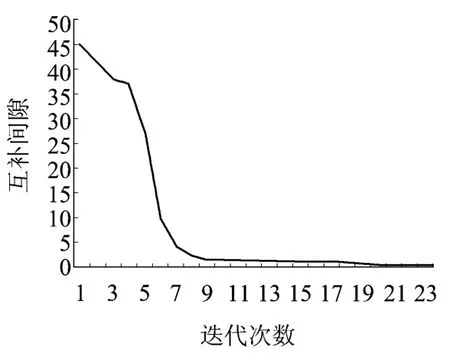
图2 国内某电网无功规划互补间隙收敛过程

预测-校正原对偶内点法经过27步迭代,耗时118 s收敛。在保证系统负荷裕度达到设定阀值的前提下,圆满地完成了以补偿量最小为目标的无功规划。

6 结语

通过建立无功规划的最优化模型,应用预测-校正原对偶内点法对其进行求解。在IEEE 14,IEEE 30,IEEE 57和IEEE 118系统和国内某个大型电网上,验证了上述模型和求解方法的有效性。

[1] 文学鸿.基于内点优化算法的电力系统静态电压稳定分析与最优控制[硕士].河海大学,2007.

[2] 陈宏伟,张兴凯,王 宽.电力系统无功优化的研究现状和展望[J].电气应用,2006(12).

[3] N.KARMARKAR.A new polynom ial-tim ealgorithm for linear programm ing[C],STOC'84 Proceedings of six teen th annual ACM symposium on Theory of computing,1984.

[4] 王锡凡.现代电力系统分析[M].北京:科学出版社,2003.

[5] 张伯明.高等电力网络分析[M].北京:清华大学出版社,2007.

[6] S.MEHROTRA.On the Imp lementation of a Primal-Dual Interior Point Method[J],SIAM Jou rnal on Optim ization,Nov.1984.

[7] 刘沛津,谷立臣,韩行.基于内点法与改进遗传法的无功规划优化混合算法[J].电力系统保护与控制,2008(17).

[8] 钟世霞,袁荣湘.内点法在电力系统中的应用述评[J].高电压技术,2005(12).

[9] 文学鸿,袁 越,鞠 平.静态电压稳定负荷裕度分析方法比较[J].电力自动化设备,2008,28(5).

[10] 王佳贤,程浩忠,胡泽春.多负荷水平下的配电网无功优化规划方法[J].电网技术,2008,(19).

[11] 吴 浩.电力系统电压稳定研究[博士].浙江大学,2002.

[12] 韦 化,丁晓莺.基于现代内点理论的电压稳定临界点算法[J].中国电机工程学报,2002,22(3):27-31.

[13] 程浩忠,吴浩著.电力系统无功与电压稳定性[M].北京:中国电力出版社.2004.