一种改进的PSO-Means聚类优化算法

魏新红，张 凯

(河南城建学院计算机科学与工程系，河南平顶山467036)

0 前言

基于粒子群的K均值聚类［1］(PSO-Means)算法是将粒子群算法［2－3］与传统的K均值算法［4］相结合，可以避免K均值算法的聚类个数K需指定的缺陷，对于线性可分的数据利用PSO能够比较精确地找到聚类的个数。但传统的PSO-Means算法在线性不可分情况下找到的聚类个数和初始聚类中心往往是不理想的［5］。在实际应用中，即使PSO算法找到了精确的聚类个数和理想的聚类质心，利用K均值算法对线性不可分问题进行聚类也不会有好的效果。

在此将核方法用在聚类研究中，对粒子的位置更新进行一些改进，即在线性空间中一个粒子的周围探测，找到在核空间中更接近最优粒子的一个点，使得这个点和该粒子之间的向量作为近似的最优方向。实验表明:这种改进具有相对较高的准确率［6］和稳定性。

1 改进的KPSO-Means算法的基本思想

核方法的主要思想是把线性空间中关于距离的计算变换成核函数的计算，即:

其中，Φ(·)为向量函数，其具体形式是不确定的;k(·，·)是满足Mercer条件的核函数。原始粒子的位置移动是由自身速度、自身最优位置和群体最优位置所决定的，由于Φ(·)不能确定，粒子在核空间中的位置和自身速度都是无法确定的。原始粒子群算法中，粒子通过式(2)更新其位置，而在核空间中，xid，vid，pid，pgd都是找不到的。

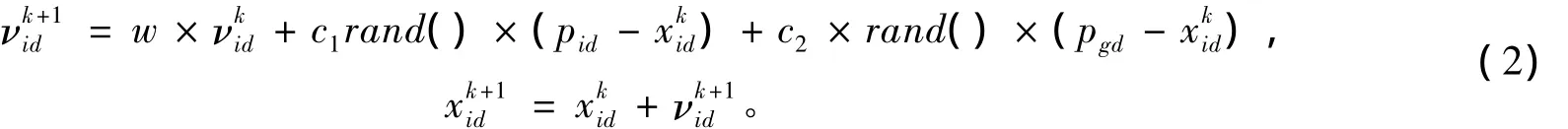
在式(2)中，最重要的是(pid－x)和(pgd－x)两个部分，分别是粒子自身的最优方向和群体最优方向。由于pid和pgd在核空间中连维数都不能确定，只能通过试探的方法找到核空间中两个最优方向在线性空间中的反映。

上面的分析说明PSO算法中最为重要的过程是粒子的移动，这个过程如果在核空间中进行就必须要求出Φ(x)的具体形式。本文提出利用模矢法的思想，依旧在线性空间中改变粒子的位置，但是最优方向的标准却来自核空间，这样就可以避免求出Φ(x)的具体形式，经过模矢法改进的PSO算法则可以用于核空间计算。具体方法是利用KPSO算法找到数据聚类的个数和初始质心，然后利用基于核函数的K均值算法在核空间中聚类。这样不但能大大的提高K均值算法的聚类能力，而且能够找到相对合适的初始质心，同时也确定了聚类个数。

2 改进的KPSO-Means算法描述

改进的算法过程如下:

①在数据空间中初始化粒子，使粒子的影响范围能够基本覆盖所有数据，并确定合适的粒子影响范围r及粒子摄动的初始步长δ1。

②每个粒子在自己的影响范围内计算自己的数据密度。遍历数据，计算粒子与数据在核空间中的距离，小于影响范围的则增加该粒子的数据密度。

③寻找自己周围的最优粒子。计算粒子与其他所有粒子在核空间中的距离，影响范围内的数据密度最大的粒子为最优粒子。

④确定两个近似最优方向p'i－xi和g'i－xi。

⑤粒子按式(2)更新位置。

⑥改变步长，返回步骤②，直到满足条件或达到最大循环次数。

⑦以KPSO算法最终得到的最优粒子为初始质心，然后进行基于核函数的K均值聚类。如果最终得到的某个类中只有极少数数据，则该类数据可以看作是孤立点。

3 实验结果与分析

在某次数据实验中通过运行PSO算法找到的聚类个数及初始质心如图1所示，然后利用KPSO算法对图1所示的数据重新查找初始聚类质心和聚类个数。粒子初始位置为在线性空间中的均匀分布。核函数采用多项式核函数: k(x，y)=(xy+1)d，d=1，2，…，N，粒子的影响范围)。最终，找到两个初始质心，一个位于外部环形中，一个位于中间接近圆心处。

4 改进的KPSO-Means算法有效性验证

以上数据试验所应用的都是二维的可视数据，为了进一步验证改进的KPSO-Means算法的有效性，在hd数据集上对算法进行测试。

运用手写数字中提取到的20维特征数据进行聚类，所用的数据集源于一项手写数字识别研究所提取到的数据［7］。手写数字识别建立在有监督分类算法基础之上，所用的hd数据集包含从0到9的10个数字。分别应用K-Means算法［8］、核K-Means［9］、PSO-Means算法和改进后的KPSO-Means算法对该数据集进行不同类别个数的聚类试验。为保证数据源的多样性，收集了多个人的笔迹。其中每个数字5 400个，共54 000个数字。手写数字经过二值化、去噪和平滑等数据处理后确定了数字的准确位置和其大小。

4.1 特征提取

本文中特征提取包括两部分的内容:穿越次数和数字形体特征。

穿越次数特征:分别在竖方向和横方向上取5条线，计算这10条线与数字交叉的次数，即穿越次数。计算方法为:穿越线上由白变黑的次数或由黑变白的次数。如图3所示，竖线1～5的穿越次数分别为1，2，3，2，1，横线1～5的穿越次数分别为2，2，1，1，1。

经过特征提取，得到了数据的20维特征，其中10维为10条穿越线的穿插越次数，10维为10条线所穿越的数字的长度与线长度的比值。

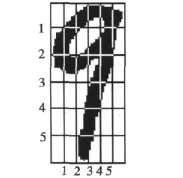
图3 特征提取

4.2 聚类质量分析

在聚类试验中，分别应用四种算法对数字0和1两类数据、2到5四类数据、0到5六类数据、0到9十类数据进行聚类。图4显示了算法随着数据集的复杂程度的增加，聚类效果的变化情况，以及在相同数据集下不同算法的聚类效果，其中横坐标表示所需聚类的手写数字的范围。

分析图4可知:随着所需聚类个数的增加，各算法的聚类正确率是减小的。在相同的数据集下，核K-Means算法和KPSO-Means算法的正确率要远高于K-Means算法和PSO-Means算法，这是由于数据集的维数较大，而且很可能是线性不可分的，因此，造成了K-Means算法和PSOMeans算法不能正确的发现数据的模式，使得聚类的正确率低下。

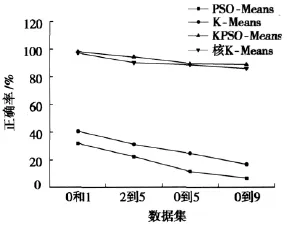
图4 聚类算法在不同数据集下的结果

5 结束语

从聚类结果可知:基于核函数的K均值算法对非线性数据聚类有着较好的聚类效果。基于核函数的改进PSO算法虽然具有一定的不适定性，但是绝大多数情况下都能找到正确的聚类个数，并且提供合适的聚类初始质心。正是因为基于核函数的改进PSO算法使得初始质心的选取避免了一定的盲目性，使得KPSO-Means算法的结果更加合理一些。本文在基于核函数的PSO算法中，粒子实际上仍是在样本空间中运行，只是运行的两个最优方向的寻找过程应用了核函数进行寻找，其收敛性还有待于进一步的研究。

［1］ 金松河，钱慎一，张素智.基于Web日志的高精度聚类算法［J］.河南科技大学学报:自然科学版，2006，27(4):49－51.

［2］ 王辉，张望，范明.基于集群环境的K-Means聚类算法的并行化［J］.河南科技大学学报:自然科学版，2008，29(4): 42－45.

［3］ 吴昌友，王福林，马力.一种新的改进粒子群优化算法［J］.控制工程，2010(5):359－362.

［4］ 但汉辉，张玉芳，张世勇.一种改进的K-均值聚类算法［J］.重庆工商大学学报:自然科学版，2009(2):144－147.

［5］ 韩凌波，王强，蒋正峰，等.一种改进的K-means初始聚类中心选取算法［J］.计算机工程与应用，2010(17):150－152.

［6］ 许建华，张学工.经典线性算法的非线性核形式［J］.控制与决策，2006，21(1):1－6.

［7］ Xiao H M，Liu C，Song ZG.Handwritten Recognition Based on Support Vector Machine［C］//Proceedings of International Forum of Information Systems Frontiers.2006 Xian International Symposium.Xian:2006.

［8］ 王慧，申石磊.一种改进的特征加权K-means聚类算法［J］.微电子学与计算机，2010，27(7):161－163.

［9］ 张莉，周伟达，焦李成.核聚类算法［J］.计算机学报，2002，25(6):587－590.