中国人口预测的半参数自回归模型

韩玉涛,杨万才,武新乾

(河南科技大学数学与统计学院,河南洛阳 471003)

0 前言

中国人口预测的模型有很多种,常用的有Logistic模型、Leslie模型、灰色模型、BP神经网络模型、线性时间序列模型等[1-4]。传统的线性模型在实际应用中往往存在设定误差,而非参数回归模型则假定变量关系未知,要对回归函数进行估计,因而能更好拟合样本数据,并对数据做出较为精确的预测,因此得到了广泛的应用[5]。巩永丽等基于核估计对中国人口增长率建立了非参数自回归模型[6];张慧芳等利用正交序列估计对中国人口建立了非参数模型[7]。

半参数模型融合了非参数模型和线性模型的优点,受到了诸多学者的广泛关注。近年来,半参数方法在人口建模中也有所应用。姜爱平等对中国人口总量建立具有外生变量的半参数自回归模型,用核估计对模型中的非参数函数进行估计[8]。该方法属于局部方法,它不能给出所拟合模型的简单显式表达式,计算量大并且运行时间较长,而多项式样条估计是全局光滑方法,能较好地克服上述核估计的弊端[9],因此本文提出基于多项式样条估计的半参数自回归模型,并对中国人口进行预测。

首先对中国 1949～2003年人口建立线性自回归模型,用最小二乘估计建立线性自回归方程;其次基于线性回归选择显著滞后变量,利用最小二乘和多项式样条方法估计半参数自回归模型中的参数向量和非参数函数,建立半参数自回归方程;最后基于建立的半参数自回归模型对中国 2004～2009年人口数据进行预测分析,并且与线性模型及Logistic模型、Leslie模型、灰色神经网络模型的预测结果进行了对比分析。

1 线性自回归模型

1.1 数据的平稳化处理

本文中用到的原始人口数据来源于中国国家统计局。由 Matlab7.0对中国1949～2008年60个原始人口数据进行做图处理,得到图1。从图1可以看到数据是不平稳的。根据线性自回归模型的要求,对原始人口数据做对数处理,再进行二次差分。若记{Yt}为中国总人口序列,{▽2ln(Yt)}为对数后二次差分序列,令Wt=▽2ln(Yt)-其中,为{▽2ln(Yt)}的均值;▽为差分符号;则 {Wt}为零均值序列,见图2所表示的序列。

1.2 数据的平稳性检验

从图2可直观的判断序列{Wt}是平稳的。为进一步说明序列的平稳性,再进行游程检验[10]。游程总数r=24,序列长度 N=53,“+”和“-”出现的次数分别为N1=25,N2=28。

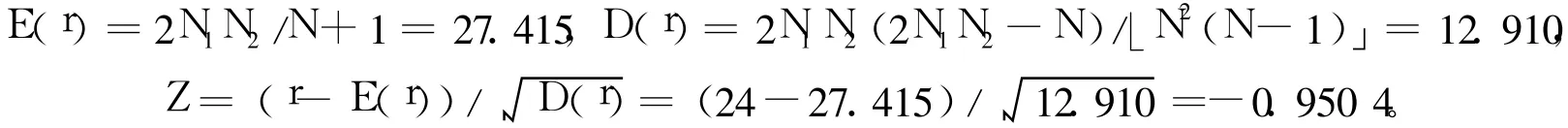
1.3 模型定阶与模型检验

用AIC,BIC准则及残差方差来确定阶数,由MATLAB运行结果(见图3和图4),可确定滞后7阶是较为理想的。

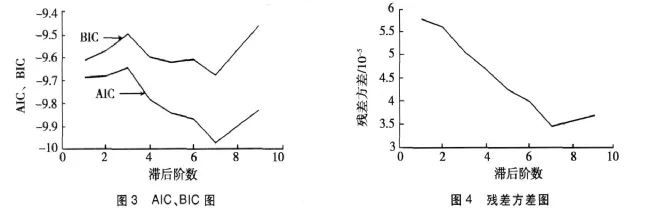
再用F检验法[9]检验线性自回归模型AR(p)的阶数。首先对{Wt}分别拟合AR(6)和AR(7)模型,两种模型的残差平方和Q1和 Q0分别为0.001 6和0.001 3,则

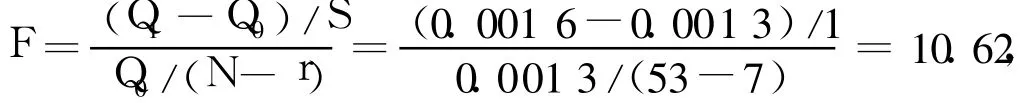
其中,S为舍弃因子的个数;N为样本容量;r为回归因子个数。给定显著性水平α=0.05,查 F分布表得Fα(1.46)=4.05,F＞＞Fα,说明AR(6)和AR(7)有显著的差异,模型阶数有上升的可能。再拟合AR(8)模型,其残差平方和为0.001 3,与AR(7)比较有:

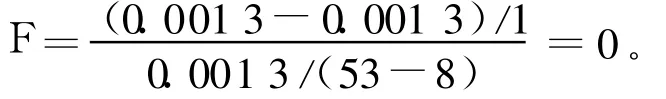
同理查表得Fα(1.45)=4.05,F＜＜Fα,故AR(7)与AR(8)没有显著差异,即选择AR(7)是合适的。

1.4 模型参数的确定

根据1.1中平稳化处理后的1951～2003年数据,对平稳序列{Wt}建立AR(7)模型,用最小二乘估计确定其中的参数,建立回归方程:

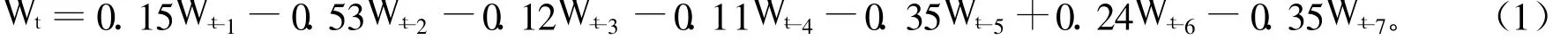
对建立的自回归方程(1)中各变量进行显著性检验,在显著性水平α=0.05下,只有Wt-2,Wt-5, Wt-7的系数是显著的(见表1)。

选取显著性变量Wt-2,Wt-5和 Wt-7,重新估计相应系数,得到线性回归方程:

方程(2)的残差平方和为0.001 7,与方程(1)比较,同上做F检验,得F=2.83＜Fα=4.05,说明两个线性自回归方程没有显著差异。

1.5 模型的适应性检验

表1 方程(1)各变量系数的显著性检验

通过计算得Q=7.66,在显著性水平α= 0.05下,查表得(4)=9.49,Q＜(7-3),说明 εt是独立的,即模型是合适的,可选取方程(2)对中国 2004～2009年人口进行预测。

2 半参数自回归模型

2.1 半参数自回归模型

其中,Yt为被解释变量;α是线性部分未知参数向量;Xt=(Xt1,…,Xtp)T=(Yt-1,…,Yt-p)T为解释性变量,线性主部把握被解释变量的大势走向;Zt=(Zt1,…,Ztq)T=(Yt-p-1,…,Yt-p-q)T,g()为未知非参数光滑函数,对被解释变量作局部调整;随机误差序列εt独立同分布且满足:E(εt)=0;Var(εt)=σ2＜∞,且εt与Ys(s＜t)相互独立。

对非参数函数估计的方法有很多种,鉴于引言部分所述多项式样条估计的优点,本文采用多项式样条估计对模型(3)中的非参数函数g()进行估计。

2.2 多项式样条估计

仅考虑紧区间[a,b]上的估计。不妨记具有结点序列a=z0＜z1＜…＜zNn＜ZNn+1=b的k次多项式样条空间为Sk,Nn,其基函数Bs()为

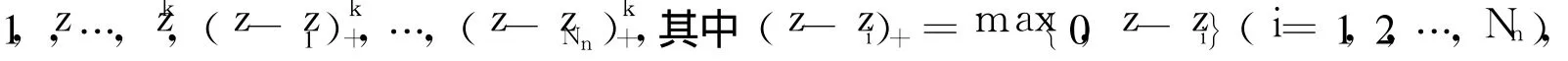
即存在一组基函数Bs()和常数βs(s=1,…,K),使得g(z)≈

其中β=(β1,…,βK)T,可得α和β的估计分别为α=(α1,…,αd)T和β=(β1,…,βK)T。从而得到g的 βsBs(z)。最小化估计值这时α和g分别为 α和 g的样条估计,详细内容可参看文献[9]。

2.3 最优方程的选取

基于线性回归选取的显著性变量,分别选取滞后 2阶、5阶和 7阶做为非参数部分,其余二变量做为线性部分,由MATLAB 7.0运行结果,得到相应的半参数自回归方程:

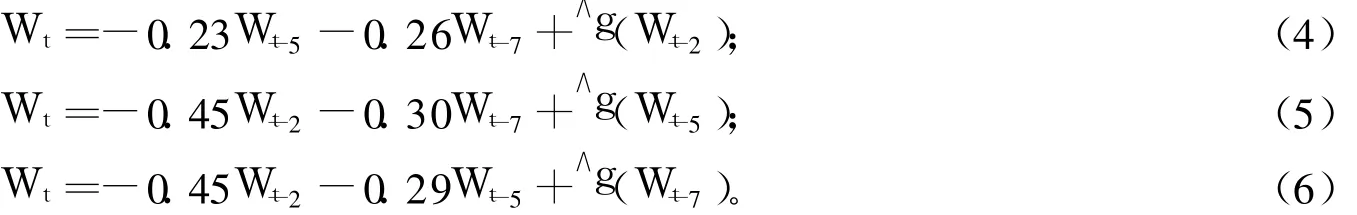
表2给出了半参数模型对人口建模使用的平稳序列{Wt}及对总人口序列{Yt}拟合与预测的均方误差。从表2可以看到:方程(4)对 1958～2003年的人口的平稳序列的拟合及总人口的拟合均方误差都最小,但是方程(5)对 2005～2008年的平稳序列{Wt}和总人口序列{Yt}的预测的均方误差最小,因此选取方程(5)与线性回归方程(2)做对比。

3 不同模型对人口预测的对比分析

3.1 线性时间序列模型与半参数自回归模型的对比

选取线性回归方程(2)与半参数自回归方程(5)分别对2004～2009年人口进行预测(见表3)。

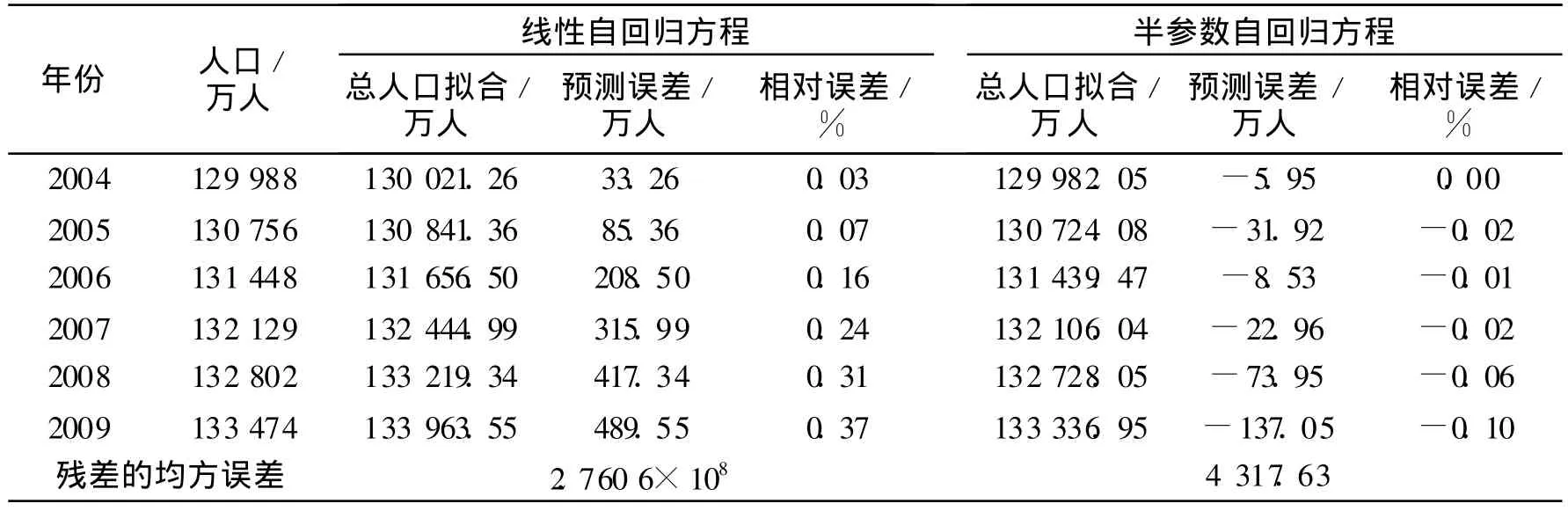
表3 线性自回归模型和半参数回归模型对 2004～2009年人口预测结果

从表3可以看到:线性模型的短期(2年)预测效果还是比较好的,但是随着年数的增加,预测误差递增的速度比较快。从第 1年误差的 33万人很快的增长到第 6年的 489万人。相对于线性自回归模型,半参数自回归模型对人口中预测精度明显较高,虽然误差也在逐年增大,但是预测 6年的误差约为线性的1/5.6、1/2.6、1/24.4、1/13.8、1/5.6、1/3.7。

3.2 半参数模型与其他模型的对比

半参数自回归模型和其他模型对中国 2005～2008年人口预测的结果进行对比(见表4)。

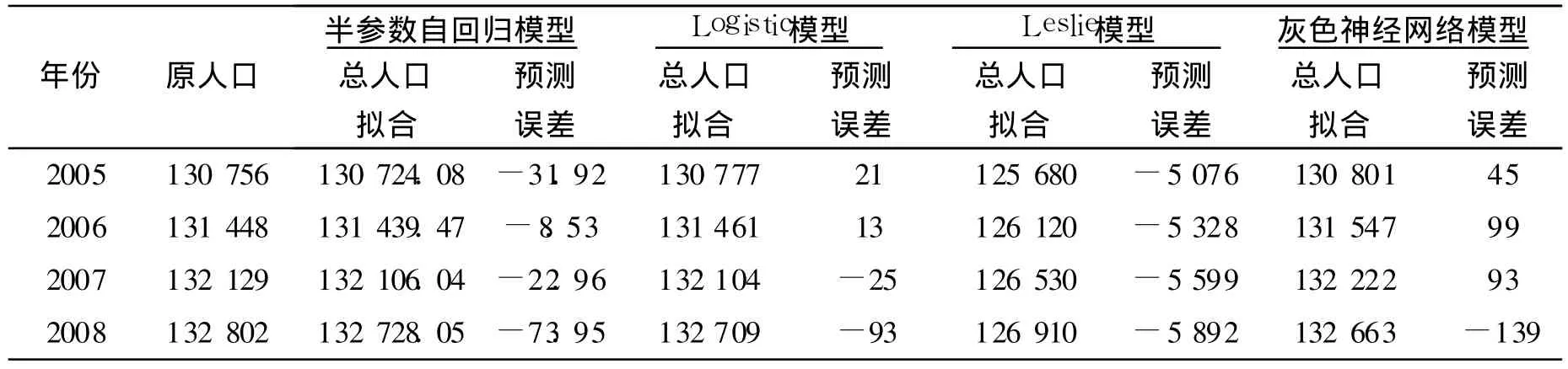
表4 几种模型对中国2005～2008年人口的预测 万人

从表4中可以看到:Logistic模型和灰色神经网络模型对人口预测的精度较高,但是半参数自回归模型的预测精度还是更高一些。

表5 半参数回归模型对2010～2013年人口进行预测 万人

最后,利用半参数自回归模型对中国 2010～2013年人口进行预测(见表5)。

4 结论

本文基于时间序列分析、半参数线性回归和非参数的多项式样条估计理论,建立中国人口的线性自回归模型和半参数自回归模型。对中国人口进行预测,半参数模型与传统的线性模型、Logistic、Leslie等模型相比,半参数自回归模型能够给出所拟合数据的显式表达式,计算量小,运行时间较快,并且预测精度也有所提高。

[1] 王学保,蔡果兰.Logistic模型的参数估计及人口预测[J].北京工商大学学报:自然科学版,2009,27(6):75-78.

[2] 陈文权,赵兹,李得胜.Leslie修正模型在人口预测中的应用[J].世界科技研究与发展,2008,30(2):219-224.

[3] 李国成,吴涛,徐沈.灰色人工神经网络人口总量预测模型及应用[J].计算机工程与应用,2009,45(16):215-218.

[4] 彭志捌.AR(p)模型在中国总人口预测中的应用[J].河北工程大学学报:自然科学版,2007,24(4):109-112.

[5] 叶阿忠.非参数计量经济学[M].天津:南开大学出版社,2003.

[6] 巩永丽,张德生,武新乾.人口增长率的非参数自回归预测模型[J].数理统计与管理,2007,26(5):769-764.

[7] 张慧芳,张德生,武新乾,等.我国人口总量的非参数预测模型[J].延边大学学报:自然科学版,2007,33(2):90-93.

[8] 姜爱平,张德生,武新乾,等.预测我国人口总量的具有外生变量的半参数自回归模型[J].河南科技大学学报:自然科学版,2007,28(1):97-100.

[9] 武新乾,田铮,韩四儿.具有外生变量部分线性自回归模型的样条估计[J].数学年刊,2007,28A(3):377-386.

[10] 王振龙.时间序列分析[M].北京:中国统计出版社,2000.