基于模糊理论的船舶减摇鳍控制系统研究

徐世杰 邢继峰 彭利坤

（海军工程大学船舶与动力学院 武汉 430033）

基于模糊理论的船舶减摇鳍控制系统研究

徐世杰 邢继峰 彭利坤

（海军工程大学船舶与动力学院 武汉 430033）

减摇鳍；模糊控制理论；船舶横摇模型

以船舶减摇鳍控制系统作为研究对象，应用模糊控制理论提出一种基于Fuzzy推理的模糊控制器并完成模糊控制器的理论实现。基于船舶横摇运动的线性方程对不同浪向下的船舶横摇运动进行了系统仿真。仿真结果表明，与常规PID控制相比，基于Fuzzy推理的模糊控制器具有更好的控制效果和更强的鲁棒性。

0 引言

减摇鳍作为主要的船舶减摇装置，目前已经在各型船舶中得到广泛的应用［1］。它能够提高船舶的耐波性、适航性、稳定性，并能延长船舶使用寿命，改善设备与人员的工作条件［2］。而减摇鳍在鳍容量和鳍型以及相应的随动系统确定后的情况下，其性能就与采取的控制策略密切相关。设计好的减摇鳍能够使船舶在设计海况下的横摇角度在5°以内。传统的减摇鳍大都采用PID控制，但是由于很难获得船舶在各种横摇干扰频率下或者在某浪向角下的最佳参数，一旦船舶航向改变或风向改变，就很难获得最佳的减摇效果［3］。

模糊控制的基本思想就是利用计算机来实现人的控制经验。与传统控制方法如PID控制相比，模糊控制可不依赖于精确的数学模型并能充分利用人类专家的控制经验，对于非线性、复杂对象的控制显示出了鲁棒性好、控制性能高的优点［4］。正是基于模糊控制的上述优点，本文设计了一个减摇鳍模糊控制器。通过在线仿真得到的结果表明，与常规PID控制相比，模糊控制器在不同海况和浪向下均可取得更好的减摇效果。

2 海浪仿真

实际海面上兴起的海浪是不规则的随机波［5］。它可以看做是由无穷多个相互独立的，具有不同幅值、频率和初相位的规则波叠加而来的。于是定点不规则长峰波可表示为：

式中：ζ（t）、ωi和εi分别为第i次谐波的波幅、角频率和初相位。

再由波高ζai与波浪谱密度Sζ（ω）的关系式：

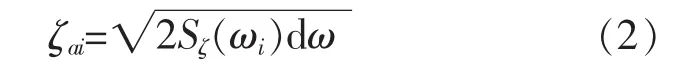
可得：

式（2）和式（3）中：

式中：ω为海浪频率（s-1）；

exp为自然对数的底e=2.718 3；

v为海面上19.5m高度处的平均风速（m/s）；

g为重力加速度（9.8m/s）。

由波倾角公式：

式中：μe为遭遇浪向角，°；

ωe为遭遇角频率：

因此，可得到作用于船体的横向波倾角为：

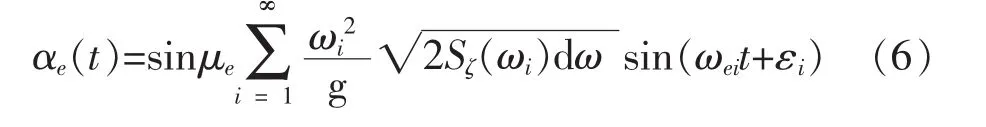
3 船体及减摇鳍系统建模

如果船舶的横摇运动角度较小，则可以应用线性横摇理论来分析船舶的横摇运动。依照Conolly的理论，船舶线性横摇可表示为［6］：

式中：Ix为相对于通过船舶质心的纵轴的惯量；

△Ix为附加转动惯量；

Νμ为每单位横摇角速度的船舶阻尼力矩；

D为船舶排水量；

h为横稳心高，m；

αe为遭遇波倾角，°；

Kc为减摇鳍产生的扶正力矩：

式中：ρ为海水密度；

AF为鳍的投影面积，m2；

CL为升力系数；

V为航速，kn。

减摇鳍的系统组成原理图如图1所示：

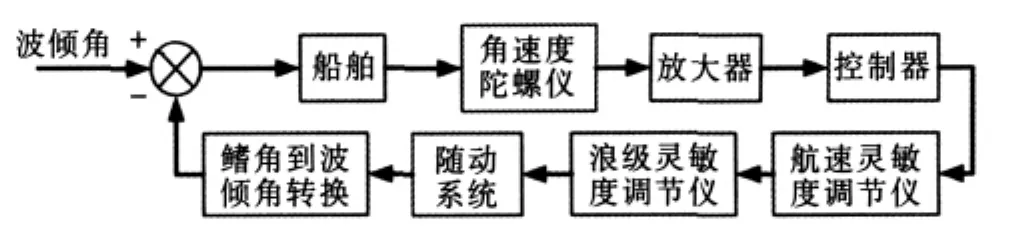
图1 减摇鳍系统组成原理图

本文选取由哈工大研制的某型减摇鳍为研究对象，各组成部分的数学模型如下：

（1）船舶模型

（2）角速度陀螺仪

角速度陀螺仪是减摇鳍控制系统中的测量元件，传递函数为：

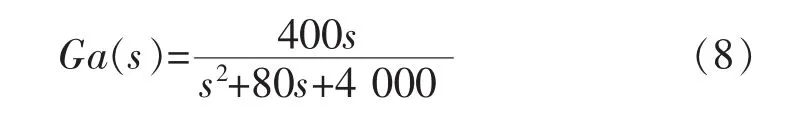
（3）放大器

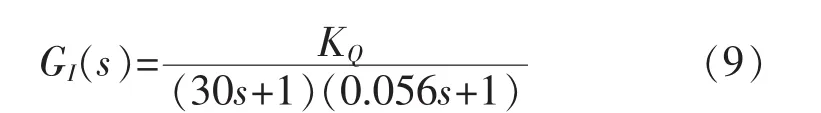
（4）航速灵敏度调节器

在设计海况下，航速调节器KH=1。

（5）浪级灵敏度调节器

在设计海况下，浪级调节器KL=1。

（6）随动系统

（7）鳍角到波倾角转换

对于NJ5型减摇鳍，从鳍角到波倾角的转换系数为：Kα=0.254 6。

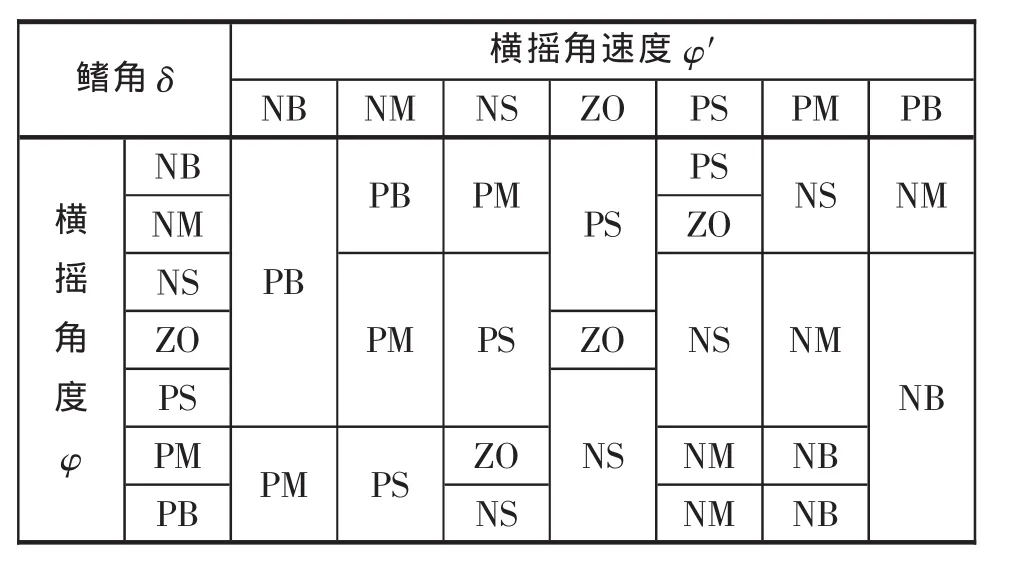
表1 模糊控制规则表

4 模糊控制器的设计

该减摇鳍模糊控制器是一个二维模糊控制器，其输入量e和e˙分别为船舶的横摇角度φ和横摇角速度φ˙，其输出量减摇鳍的鳍角δ。横摇角φ和横摇角速度φ˙均划分为7个模糊集合{NB，NM，NS，ZO，PS，PM，PB}，并且论域均为A=［-5，-4，-3，-2，-1，0，1，2，3，4，5］，隶属度函数采用三角分布的隶属函数［7］。根据以往对减摇鳍控制可以总结出如下一些经验规则，例如：

（1）如果船向左边偏一个较大角度，并且角速度也向左边较大，则减摇鳍的左鳍打一个较大的正攻角，右鳍打一个相反的攻角；

（2）如果船向左边偏一个较小角度，并且角速度也向右较小，则对减播鳍不加控制；

（3）如果船向左边偏一个较小角度，并且角速度也向右较大，则减摇鳍的左鳍打一个较大的负攻角，右鳍打一个相反的攻角。

根据上述设计思想可得到如表1所示的控制规则。各规则中，使用Zadeh的模糊逻辑and操作，采用Centroid反模糊化方法得到鳍角δ。限于篇幅，各三角隶属函数曲线没有给出，在Matlab中利用模糊逻辑工具箱很容易实现。

5 系统仿真及结果分析

在Matlab软件环境下利用Simulink工具箱建立仿真程序如图2所示［8］。

图2 减摇鳍模糊控制仿真程序图

在不同海况下仿真得到的PID与模糊控制的船舶横摇角对比如图3所示。

由以上得到的仿真曲线可以得出如下结论：

（1）与传统PID控制相比，采用模糊控制器后船舶的横摇角度显著地降低；

（2）在各种海况下模糊控制器均可得到比传统PID更满意的控制效果，即模糊控制器的鲁棒性更强。

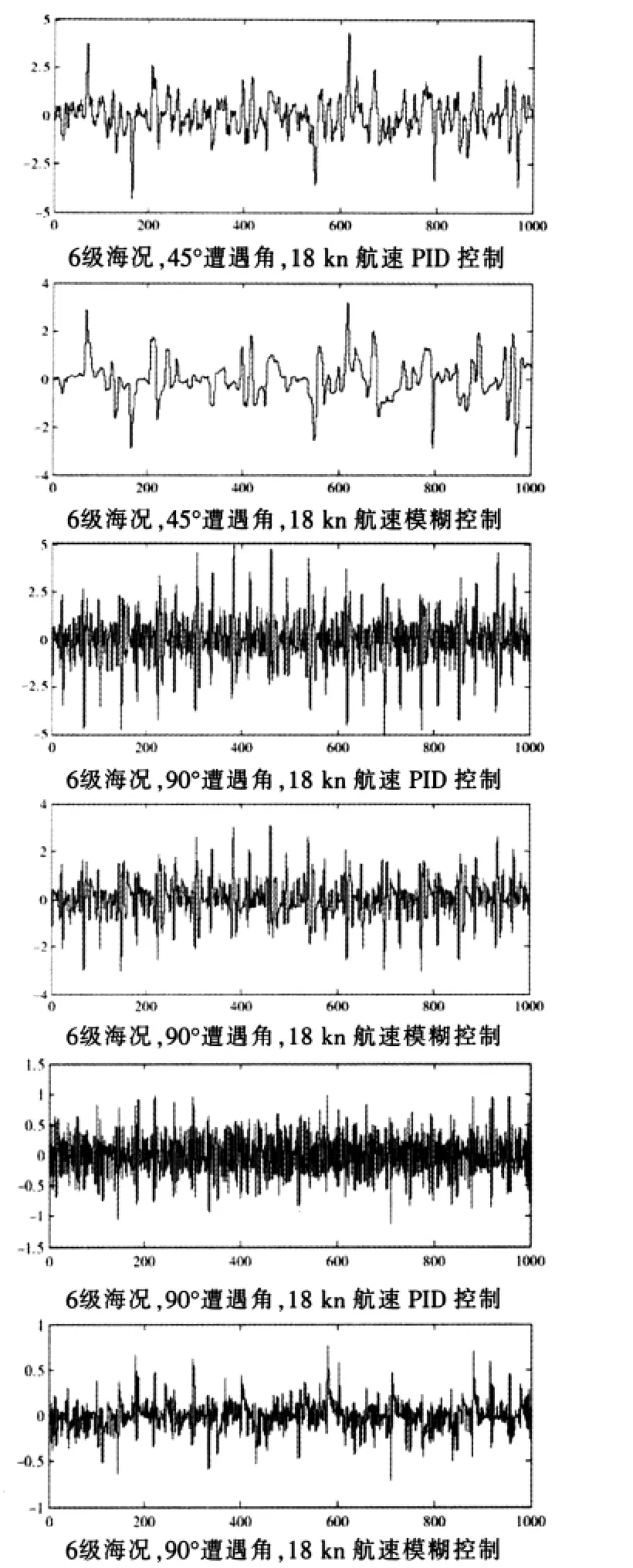
图3 仿真曲线

［1］许可建，刘维亭，朱志宇，张冰.船舶减摇控制方法综述［J］.船舶，2004，14（5）：14-17.

［2］金鸿章，李国斌.船舶特种装置控制系统［M］.北京：国防工业出版社，1995.

［3］金鸿章，王科俊，吉明.智能技术在船舶减摇鳍系统中的应用［M］.北京：国防工业出版社，2003.

［4］李国勇.智能控制及其Matlab实现［M］.北京：国防工业出版社，2005.

［5］邱宏安.随机海浪模型的建立及仿真分析［J］.系统仿真学报，2000，12（3）：13-15.

［6］王科俊.海洋运动体控制原理［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［7］杨纶标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，2005.

［8］邓薇.MATLAB函数速查手册［M］.北京：人民邮电出版社，2005.

Fuzzy-based control system of fin stabilizer

XU Shi-jie XING Ji-feng PENG Li-kun
（Naval University of Engineering，College of Naval Architecture and Marine Power，Wuhan 430033，China）

fin stabilizer；fuzzy-control theory；model of ship motion

In this paper，a fuzzy inference controller based on fuzzy theory is studied and implemented theoretically.The ship roll with different wave direction is simulated by solving the linear equation of ship roll.The simulation results indicate that the fuzzy-based control system of fin stabilizer is better and more robust than general PID controller.

U661.32

A

1001-9855（2011）03-0024-03

2011-03-12

徐世杰（1986-），男，硕士研究生，研究方向：船用机电液设备控制与仿真。

邢继峰（1960-），男，教授，博士研究生导师。研究方向：数字液压技术、并联机器人技术、舰艇操纵控制与仿真等。

彭利坤（1975-），男，博士研究生，副教授，研究方向：机电液控制与仿真、并联机器人技术等。