组合结构箱梁扭转极限承载力计算方法研究
2011-04-02张长青安永日安里鹏
张长青,安永日,安里鹏
(1.招商局重庆交通科研设计院有限公司,重庆 400067;2.重庆交通大学土木建筑学院,重庆 400074)
组合结构箱梁扭转极限承载力计算方法研究
张长青1,安永日1,安里鹏2
(1.招商局重庆交通科研设计院有限公司,重庆 400067;2.重庆交通大学土木建筑学院,重庆 400074)
对受扭组合结构箱梁进行理论分析,提出了配筋率与混凝土破坏模态和钢筋屈服模态之间的相互关系。提出了组合结构箱梁的扭转极限承载力计算方法。通过与实验结果进行比较,验证了所提出计算方法的正确性。
组合结构箱梁;扭转;极限承载力
组合结构梁与预应力混凝土梁相比,具有自重轻、施工方便、避免腹板开裂、缩短工期等优点。与钢箱截面梁比较,具有刚度大、用钢量少、受压区发挥混凝土抗压性能等优点。据研究[1],组合结构与钢结构相比较,可节约用钢量20% ~40%,挠度可减少1/3~1/2。正因为上述原因,目前组合结构桥梁迅速得到应用,是桥梁主要发展的方向之一。目前在国内已建好的组合结构桥梁[2](不包含波形钢腹板)有20余座。波形钢腹板组合结构桥梁,已建造的有13座,正在建造的有20余座[3]。
组合结构箱梁的抗弯极限承载力的计算,采用与混凝土结构同样计算方法。抗剪极限承载力计算,采用了忽略顶底板混凝土,只有钢腹板承担剪力的假定[4]。而对扭转极限承载力,目前在国内外设计规范和设计指南中都没有明确提出计算方法。组合结构箱梁扭转弯矩的验算有,把剪力产生的腹板剪应力和扭矩产生的腹板剪应力叠加,与容许应力比较的方法[4]。
对组合结构箱梁扭转极限承载力,聂建国[5]、Y.L.Mo,等[6]提出了受扭时的混凝土本构关系,然后用有限元分析计算扭转极限承载力方法。他们所提出的计算方法需要有限元模拟,不能直接求出扭转极限承载力,给设计者带来了一定难度。另外,李宏江[7]、王文,等[8]研究了扭转与畸变效应。
笔者通过理论分析,确定了组合结构箱梁自由扭转时的2种破坏模态,即混凝土压坏模态、钢筋屈服模态与配筋率之间的相互关系。并且,提出了组合结构箱梁自由扭转极限承载力的简化计算方法。在计算方法中,还用库伦摩擦理论考虑了体外预应力索及无黏结体内预应力索的张拉力对扭转极限承载力的影响。最后,通过计算结果与实验进行比较,验证了所提出的计算方法的可靠性。
1 自由扭转极限承载力计算
组合结构箱梁的顶底板参考 P.Lampet和 B.Thuerlimann提出的变角度空间桁架模型[9]。其模型基本假定如下:①混凝土顶底板裂缝分成一系列倾角为α的斜杆;②顶底板的纵向钢筋和横向钢筋构成桁架拉杆;③不计钢筋的销栓作用;④原有混凝土箱梁桁架模型中的混凝土腹板部分,由钢腹板承担。
根据闭口薄壁杆件理论,有扭矩T在截面侧壁中产生的剪力流q可表示为:

式中:T为扭矩;Tf为翼缘承担扭矩;Tw为腹板承担扭矩;A为截面各壁中线所围成的面积,A=b×h(b为腹板中心之间间距;h为上下翼缘板中心之间间距);q为剪力流。
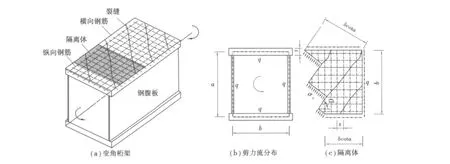
图1 变角度空间桁架模型Fig1.Variable angle dimensional truss model
1.1 混凝土翼缘承担扭转极限承载力计算
从组合结构箱梁顶板中,取阴影部分为隔离体如图1(a),图中由轴向的力平衡,可得:
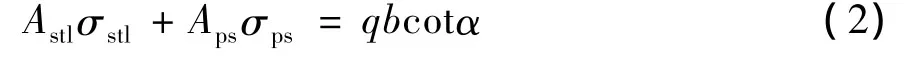
式中:Astl为翼缘板纵向钢筋面积;σstl为翼缘板纵向钢筋的拉应力;Aps为翼缘板预应力筋面积;σps为翼缘板预应力筋拉应力;α为翼缘板裂缝角度。
同样方法,从隔离体的横向的力平衡,可得:

式中:Astv为单排横向钢筋面积;σstv为横向钢筋拉应力;s为横向钢筋间距。
从式(2)和式(3)中消去q,可得:

式中:Tf1为由钢筋屈服达到极限状态时混凝土翼缘板承担的扭矩。
根据混凝土裂缝方向的力平衡,可得:

式中:σc为混凝土压应力(参考图1);t为隔离体厚度。
整理式(7),可得:

由式(8),翼缘承担的扭矩与混凝土压应力关系如下:
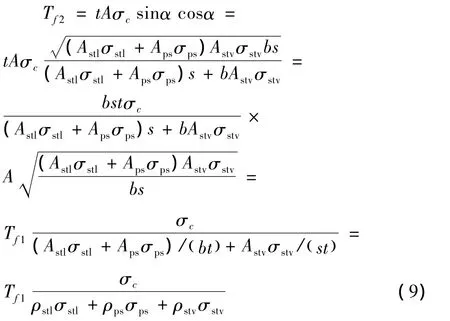
式中:Tf2为由混凝土压破达到极限状态时混凝土翼缘板承担的扭矩;ρstl为纵向钢筋的配筋率;ρstv为横向钢筋配的筋率;ρps为预应力筋的配筋率。
假设纵向钢筋和横向钢筋的总配筋率为200 kg/m3,预应力筋配筋率为50 kg/m3,钢筋屈服强度为335 MPa,预应力筋屈服强度为1 581 MPa,混凝土抗压强度为 26.8 MPa,并折减 0.85[6],并带入式(9),可得:

从式(10)中可以看出,在常规配筋率的情况下,混凝土达到抗压强度之前钢筋先达到屈服强度,截面破坏模态为钢筋屈服。
1.2 钢腹板承担扭转极限承载力计算
钢腹板承担扭矩可按式(11)计算:

式中:tw为钢腹板厚度;τw为钢腹板剪应力(小于剪切屈服强度)。
1.3 预应力对扭转极限承载力的影响
在扭转极限承载力的计算中,考虑预应力影响。其基本假定如下:①体外预应力筋和无黏结体内预应力筋的张拉力作用于翼缘板混凝土开裂面;②预应力张拉力由混凝土开裂面的摩擦力形式抵抗扭矩;③其摩擦力遵守库伦摩擦法则;④忽略约束扭转和畸变效应。其抵抗扭矩,可按式(12)计算:

式中:Tp为体外预应力索及无粘结体内预应力索抵抗扭矩;μ为库伦摩擦系数;P为预应力张拉力。
2 计算结果与实验结果比较
实验模型[6]的截面如图2,钢筋混凝土顶底板的宽度为80 cm,截面高度为45 cm,顶底板混凝土厚度为10 cm,波形钢腹板厚度为15 mm。顶底板纵向钢筋间距为9.5 cm,直径为9.5 mm,布置两层。横向钢筋间距为11 cm,直径为6.4 mm。
实验模型如表1,根据混凝土抗压强度和预应力筋的预加力,分为4种类型。其材料参数见表1。

图2 试验模型截面Fig.2 Cross section of experimental model

表1 实验模型材料参数Tab.1 Material parameters of experimental model

表2 扭转极限承载力Tab.2 Ultimate strength of torsional moment
扭转极限承载力的实验和计算结果的比较见表2。表中:Tt为实验结果;Ta为不考虑预应力效应时的计算结果;T'a为考虑预应力效应时的计算结果。考虑预应力效应时,混凝土裂缝之间的库摩擦系数取 0.5[10]。
把进行实验模型N系列和H系列的实验结果进行比较,虽然混凝土强度分别提高了1.36倍和1.39倍,但扭转极限承载力只提高了1.05倍和1.03倍,其效果不明显。这与1.1节的理论分析中,常规混凝土结构由钢筋屈服达到扭转极限状态,混凝土强度不影响其承载力的结果基本吻合。
为考察预应力对扭转承载力的效应,比较实验模型5系列和8系列的实验结果,扭转极限承载力分别提高了1.08倍和1.07倍,比提高混凝土强度的效果明显。
比较实验结果和忽略预应力时的计算结果,实验结果为计算结果的1.09~1.22倍,相差较大。比较实验结果和考虑预应力时的计算结果,实验结果为计算结果的1.01~1.08,计算结果偏小。其主要原因为,简化计算中未考虑钢筋的硬化、钢筋的销栓作用等。但计算良好地反映了实验结果,而且偏于安全。
3 结论
通过对组合结构箱梁的理论分析和实验结果的比较,得到以下结论:
1)提出了组合结构箱梁的2种破坏模态(混凝土压坏模态和钢筋屈服模态)和配筋率之间的相互关系公式;
2)在常规配筋率的情况下,一般由钢筋屈服达到扭转极限状态;
3)提出了体外预应力及无黏结体内预应力效应计算公式;
4)用提出的简化计算公式计算的抗扭进行承载力,良好地反映了实验结果,而且偏于安全。
在扭转承载力简化计算公式中未考虑混凝土强度的变化,需要进一步的研究。并且,实验数据偏少,需要用更多的实验数据验证简化计算公式的准确性。
[1] 林伟伟.钢-混凝土组合弯箱梁桥结构行为研究[D].西安:长安大学,2006.
[2]孙洪超.大跨度钢-混凝土组合结构桥梁全寿命性能研究[D].北京:北京建筑工程学院,2010.
[3]万水.波形钢腹板PC组合箱梁桥设计与施工[R]∥波形钢腹板PC组合结构桥梁技术研讨会.成都:[出版者不详],2010.
[4]日本高速道路技术中心.日本波型钢腹板桥设计:施工指南[S].日本:日本高速道路技术中心,2004.
[5]聂建国,唐亮.波形钢腹板PC组合箱梁纯扭性能的非线性分析[J].中国公路学报,2007,20(5):71-77.
NIE Jian-guo,TANG Liang.Nonlinear analysis of pure.torsion property for prestressed concrete composite box girders with corragated steel webe[J].China Journal of Highway and Transport,2007,20(5):71-77.
[6]Mo Y L,Jeng,Chyuan-hwan,Chang Y S.Torsional behavior of prestressed concrete box-girder bridges with corrugated steel webs[J].ACI Struct Journa,2000,97(6):849-859.
[7]李宏江,叶见曙,万水,等.波形腹板箱梁的扭转与畸变分析及试验研究[J].桥梁建设,2003(6):1-4.
LI Hong-Jiang,YE Jian-shu,WAN Shui,et al.Analysis and exeperiment al study of torsion and distortion of box girder with corrugated steel webs[J].Bridge Construction,2003(6):1-4.
[8]王文.波形钢腹板箱梁扭转效应和畸变效应的分析与模型试验研究[D].长沙:湖南大学,2008.
[9]顾祥林.混凝土结构[M].上海:同济大学出版社,2007.
[10]JTG D 63—2007公路桥涵地基与基础设计规范[S].北京:人民交通出版社,2007.
Study on Calculation Method of Ultimate Strength of Torsional Moment of Composite Steel Box Girders
ZHANG Chang-qing1,AN Yong-ri1,AN Li-peng2
(1.Chongqing Communications Research & Design Institute Co.,Ltd.,China Merchants Bureau,Chongqing 400067,China;
2.School of Civil Engineering & Architecture,Chongqing Jiaotong University,Chongqing 400074,China)
Theoretical analysis of the composite steel box girders subjected to torsional moment was proceeded.The relationship between reinforcement rate and concrete failure modes,reinforced bar yield failure modes was put forward.Meanwhile,the calculation method of ultimate strength of composite steel box girders was presented.The correctness of calculation method was verified by comparison with experimental results.
composite steel box girders;torsional moment;ultimate strength
U448.21+6
A
1674-0696(2011)03-0369-03
2011-02-14;
2011-03-20
张长青(1971-),男,重庆人,副研究员,工程硕士,主要从事桥梁设计方面的研究。E-mail:zhangchangqing@cmhk.com。
