低空雷达导引头海面目标检测性能分析

杨 勇 冯德军 王雪松 张文明 肖顺平

(国防科技大学电子科学与工程学院 长沙 410073)

1 引言

利用低空和超低空飞行来实施突防是反舰导弹常用的一种攻击手段。反舰导弹低空飞行降低了敌方雷达发现自身的概率，与此同时，低空飞行带来的多径效应明显、海杂波强度大等问题也给反舰导弹自身探测目标带来了不利影响。雷达导引头有效检测出目标是后续跟踪的前提，分析反舰导弹低空突防时雷达导引头的检测性能是提高其检测性能、保证其稳定跟踪目标直至有效命中目标的关键。

低空雷达导引头检测海面目标面临两种不利因素：一种是强海杂波，另一种是多径散射。海杂波使得检测门限提高，可能造成目标难以检测；多径效应导致雷达导引头在某些距离段的目标回波衰减或增强，影响雷达导引头的目标检测性能。研究低空突防下的雷达导引头面临的海杂波特性和多径效应对分析、提高雷达导引头的检测性能无疑具有指导性意义。文献[1,2]基于电磁散射理论研究了低掠射角下海面的散射特性。文献[3-7]基于实测数据，研究了海杂波特性及建模方法，通过对大量实测数据的统计分析，发现低掠射角下的海杂波幅度分布具有较长拖尾，K分布能够较好地与实测数据相吻合。低空环境下，雷达导引头多径效应明显，镜反射与漫反射同时存在，且以镜反射为主。虽然镜反射导致的多径效应对雷达导引头跟踪具有不利影响[8−13]，但对雷达导引头的检测可能有利[14]。单纯研究海杂波或多径环境下雷达导引头检测性能的文献较多，但在一种场景下同时考虑海杂波和多径散射，对雷达导引头的检测性能进行分析的文献还未曾见。

本文立足于分析低空雷达导引头检测海面目标的检测性能，为后续研究如何提高低空雷达导引头目标检测性能作铺垫。文章充分考虑了低空雷达导引头所面临海杂波和多径环境，对多径散射和低掠射角下的海杂波进行了详细建模，在此基础上，仿真分析了雷达导引头检测不同大小目标的性能。文章第2节建立了多径散射的镜反射和漫反射模型，第3节给出了低掠射角下海杂波建模方法，第4节结合具体场景，仿真分析了低空飞行雷达导引头检测海面不同大小目标的性能。

2 多径效应

2.1 镜反射

镜面反射模型分为两种，一种考虑一路反射信号，地球表面为一平面，地面平坦并有良好导电性。另一种考虑三路反射信号，地球表面为一曲面，地面具有一定粗糙度。镜面反射示意图如图1所示，一路反射模型考虑ABA, ABOA两路目标回波信号，三路反射信号模型考虑ABA, ABOA, AOBA和AOBOA四路目标回波信号，因此，后种模型比前种模型多考虑两路目标回波信号，两种模型得到的目标回波信号幅度不同，而针对雷达导引头检测环节，目标回波幅度大小直接影响着雷达导引头的检测性能，采用一路反射模型并不能真实反映雷达导引头接收的目标回波信号，因此，本节采用第2种镜面反射模型。

针对三路反射信号镜反射模型，雷达接收的目标回波信号可表示为

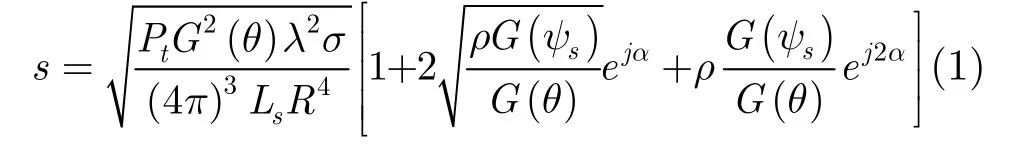
其中Pt为雷达导引头的发射功率，λ为发射信号波长，σ为目标RCS, Ls为收发损耗，R为雷达导引头与目标之间的距离，G(θ), G(ψs)分别为目标和反射点方向的天线增益，ρ为镜面反射系数，α为反射路径与直达路径的相位差。

考虑到地球曲率和地面粗糙度，镜面反射系数表示为

其中ρ0为菲涅尔反射系数，D为发散因子，

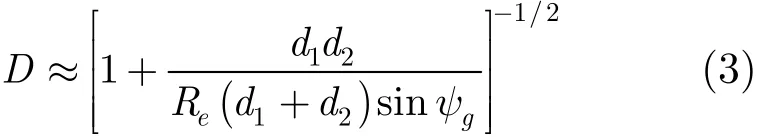
Re为4/3倍的地球半径，d1, d2分别为反射点到雷达导引头和目标之间的地面距离，ψg为反射点处的掠射角。

式(2)中，ρs为粗糙表面反射系数的均方根值，表示为

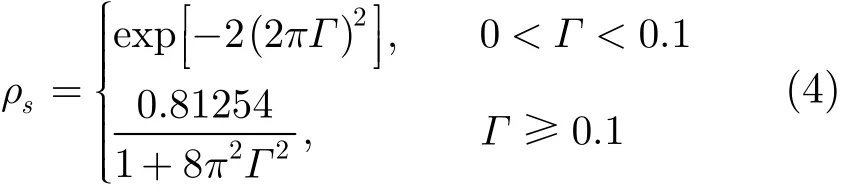
其中Γ=(σhsinψg)/λ, σh为海面高度的标准偏差。

反射波与直达波的相位差

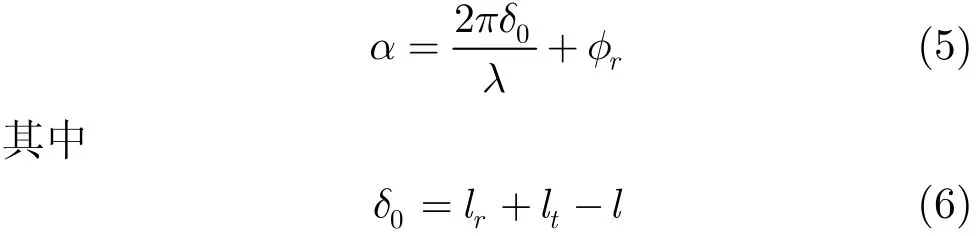
φr为反射系数的相位，lr、lt分别为反射点到雷达、目标的距离，l为雷达目标间的距离。

随着目标的运动，镜反射点在不断变化。镜反射点的精确求解是计算目标回波信号的基础，反射点的位置可通过求解下列方程组得到

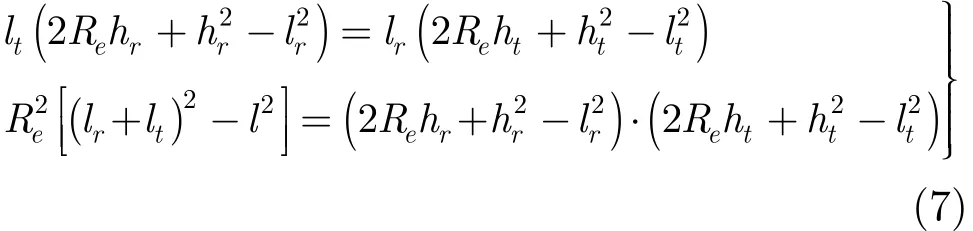
在已知天线高度hr、目标高度ht和它们之间距离l的前提下，式(7)唯一确定了反射路径lr和lt的长度，即确定了镜反射点的位置。

在本文中，假定雷达导引头以高度hr朝着目标飞行，速度为vr，雷达目标间的初始距离为R0，目标高度和位置固定不变。以地球中心为圆心，雷达导引头与目标之间的初始距离对应的圆周角为

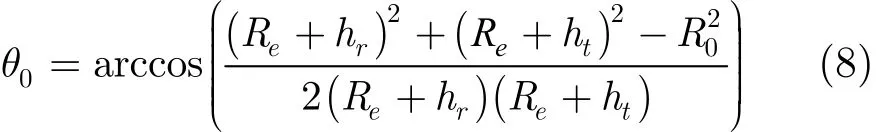
t时刻雷达导引头飞过的圆周角为

t时刻雷达导引头与目标间距离对应的圆周角为

则t时刻雷达导引头与目标间距离为

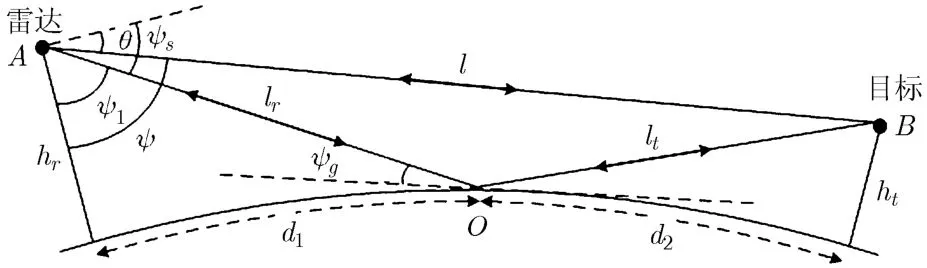
图1 镜面反射示意图

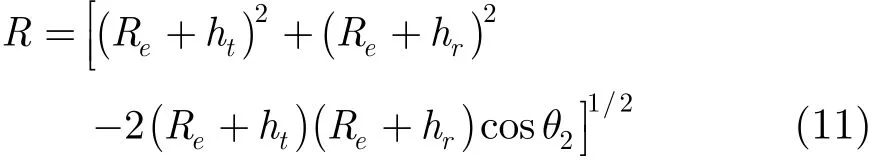
于是图1中

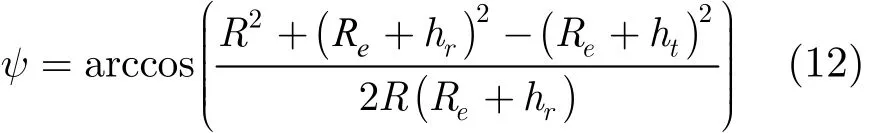
则目标俯仰角

反射点处的掠射角可表示为

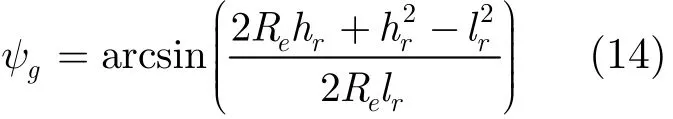
镜像目标的俯仰角为

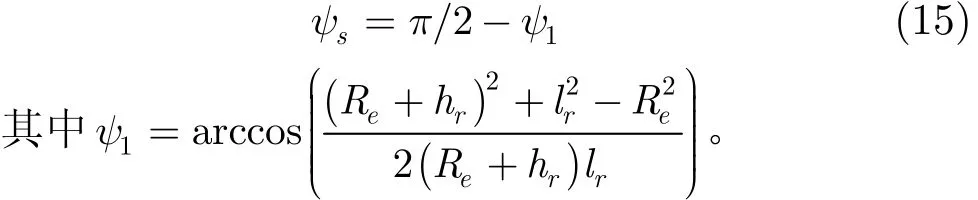
2.2 漫反射

漫反射随机性较高，漫反射建模通常先获得实验数据，然后基于数据拟合出近似模型。漫反射模型分为3种：一种将漫反射视为高斯-马尔可夫过程，该模型对实验数据的依赖性较高；另一种认为漫反射集中在一闪烁面，建模时，先对闪烁面边界进行确定，然后将闪烁面划分为10块左右的距离单元，最后将生成各距离单元回波信号进行叠加，从而得到漫反射回波信号[13]；第3种模型认为漫反射集中在一扩展的闪烁面，该闪烁面较第2种的大，其将闪烁面细分为60×32个网格，然后将各散射单元回波信号叠加，得到漫反射回波信号[15]。文献[15]对各种漫反射模型分别进行了建模分析，并将各种模型应用于导弹性能评估仿真系统中，通过对比发现：第1种模型只适用于海况较低的情况；第2种模型能够较好的适应各种海况，与实验数据吻合较好；第3种模型与第2种模型效果相当，但计算量大，运行效率较低。结合实际背景，本文采用第2种漫反射模型。

闪烁面的形状、大小由天线高度、目标高度、弹目距离、雷达波长以及反射面的高度分布所决定，闪烁面示意图如图2所示。

闪烁面被划分为若干个距离单元，各距离单元的边界可由式(16)计算得到[13,15]

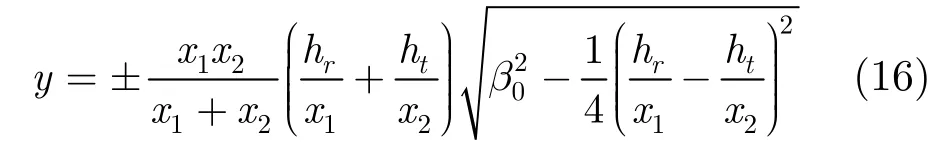
其中x1、x2分别为某一距离单元到雷达导引头和目标的地面距离，β0为闪烁面内的最大坡度。

图2 漫反射及闪烁面示意图

对于低掠射角情况，θ＜β0≪1, ht＜hr≪R ，闪烁面的范围为[xa, xb][13]，其中xa=hr/2β0, xb=R−hr/2β0。

反射面粗糙性用粗糙度因子表示为

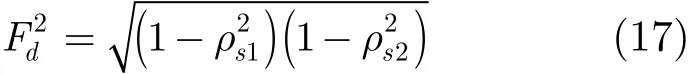
式中ρs1、ρs2分别为入射、反射路径的镜面反射系数均方根值。

漫反射信号可表示为

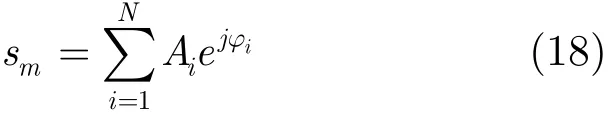
其中N为闪烁面内的距离单元数，N通常取为10,iA、ϕi分别为经第i个距离单元反射的目标回波幅度和相位。

经第i个距离单元反射后的目标回波幅度

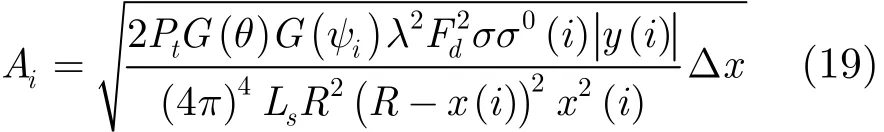
其中x(i)为第i个距离单元与雷达导引头之间的距离，σ0(i)为第i个距离单元的前向散射系数，Δx=(xb−xa)/N 为距离单元的宽度。漫反射信号的相位具有较强的随机性，通常假定经闪烁面反射的回波信号相位ϕi服从[0,2π]的均匀分布。

若根据雷达导引头位置计算得到的闪烁面超过了雷达导引头的视线范围，则闪烁面内的距离单元数为

式中xh为雷达导引头的视线距离。

3 海杂波建模

海杂波的强度决定着雷达导引头的检测门限，海杂波的建模直接影响着目标检测结果。随着对海杂波认识的逐渐深入，发现常规的高斯分布、瑞利分布等与实测低掠射角下的海杂波幅度分布存在一定差异，对雷达在低掠射角工作时获得的海杂波回波包络模型的研究表明，K分布不仅可以在很宽的范围内很好地与观测杂波数据的幅度分布匹配，而且还可以正确的模拟杂波回波脉冲间的相关特性[6,7]。

海杂波的功率谱采用高斯型来表示[16]：

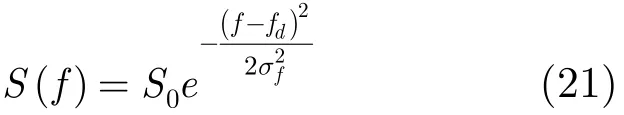
其中S0为海杂波平均功率，fd为海杂波平均多普勒频率，σf为其功率谱标准离差。

本文联合采用基于距离单元划分和零记忆非线性变换(ZMNL)方法生成海杂波数据。具体步骤如下：

(1)根据雷达参数和目标位置，确定生成杂波的地域范围，在径向和方位向划分距离散射单元；

(2)根据雷达-散射单元几何关系，计算各散射单元回波信号，对同一距离分辨单元的回波信号进行合成(在中重频和高重频情况下，考虑距离单元模糊)；

(3)以步骤(2)中计算得到的各距离单元杂波幅度为均值，采用ZMNL方法生成CFAR各参考单元海杂波数据。

在计算各散射单元回波时，海面散射系数σs采用根据实测数据修正的低掠射角下海面散射系数模型[16]：

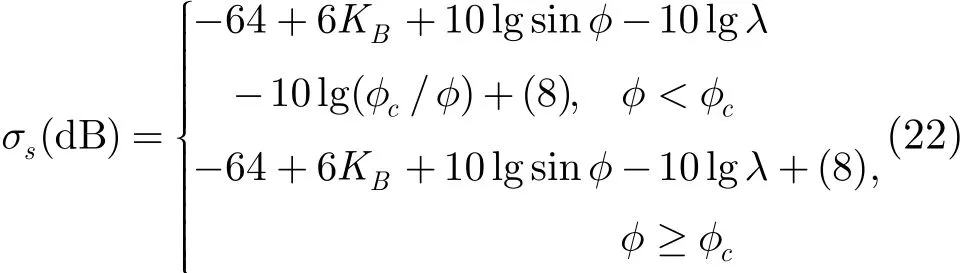
其中KB为蒲氏海况级数，φ为距离单元对应的掠射角，φc=sin−1(λ/(2h1/10))是入射余角的临界角，h1/10是1/10主效浪高。式(22)的约束条件为KB=3,HH极化在X, C, S波段时加入最后一项“(8)”，其它海况下的σs，海况增加(减少)一级，C, S, L波段分别以±6 dB, X波段以±8 dB为增量。对于VV极化在海况1, 2时X, C波段σs比HH极化时增加5 dB,S波段增加12 dB,L波段增加8 dB；海况3, 4时X, C波段增加3 dB,S, L波段增加5 dB；海况5-7时X, C波段增加2 dB, S, L波段增加5 dB。

4 仿真结果与分析

雷达发射简单脉冲串信号，发射峰值功率为50 kW，波长为3 cm，脉冲重复频率为2 kHz，脉宽为1 μs，天线最大增益为33 dB，半功率波束宽度为2°，天线俯仰向和方位向方向图均用辛克函数进行建模，雷达收发损耗为3 dB。海况为3级，雷达导引头高度为100 m，速度为300 m/s，海面目标高度为10 m，目标固定不动，雷达导引头在距离目标50 km处开机，并以恒定高度朝目标方向飞行。仿真中，接收机热噪声相对杂波功率较小，可忽略；雷达导引头采用单脉冲平均单元CFAR检测，参考单元数为16，保护单元数为2。单脉冲检测的流程图如图3所示。

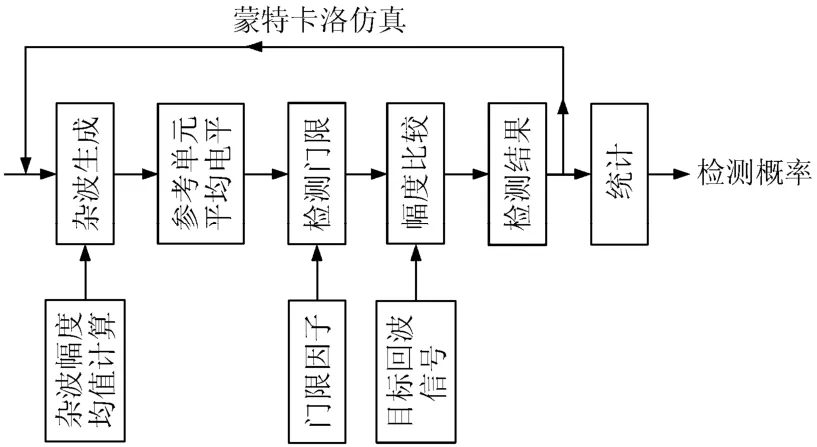
图3 单脉冲检测信号处理流程图

为了研究多径散射、海杂波对雷达接收信号的影响，假定雷达导引头在飞行过程中，天线方位向始终对准目标，俯仰向保持水平。镜面反射和漫反射对雷达导引头接收信号的影响效果用接收信号功率差来表示，接收信号功率差表示为

其中sr(dBW)为目标直达波与多径回波叠加后的回波功率，sd(dBW)为目标直达波的回波功率。镜面反射和漫反射引起的接收信号功率差如图4所示。

在研究镜反射对雷达接收信号影响时，假定雷达接收信号为直达波信号与镜反射信号的相干合成。从图4(a)可以看出，镜反射回波功率强，导致雷达接收信号起伏较大，随着雷达导引头与目标间距离的变化，接收信号呈现出被衰减和被增强交替出现的现象。接收信号功率增强最高可达10 dB，衰减最大可达27 dB。可见，低空下的镜反射效应对雷达导引头的接收信号影响十分明显。在研究漫反射对雷达接收信号影响时，雷达接收信号为直达波与多路漫反射信号的相干合成。海面漫反射对雷达接收信号功率的增强或衰减效果保持在0.2 dB左右，如图4(b)所示。这种情况下，漫反射信号虽然存在，但对雷达导引头接收到的目标回波信号影响不大，对目标检测不会造成影响，因此，漫反射效应可以忽略。以上说明：X波段雷达导引头在100 m高度探测海面目标时，多径散射以镜反射为主、漫反射可忽略。

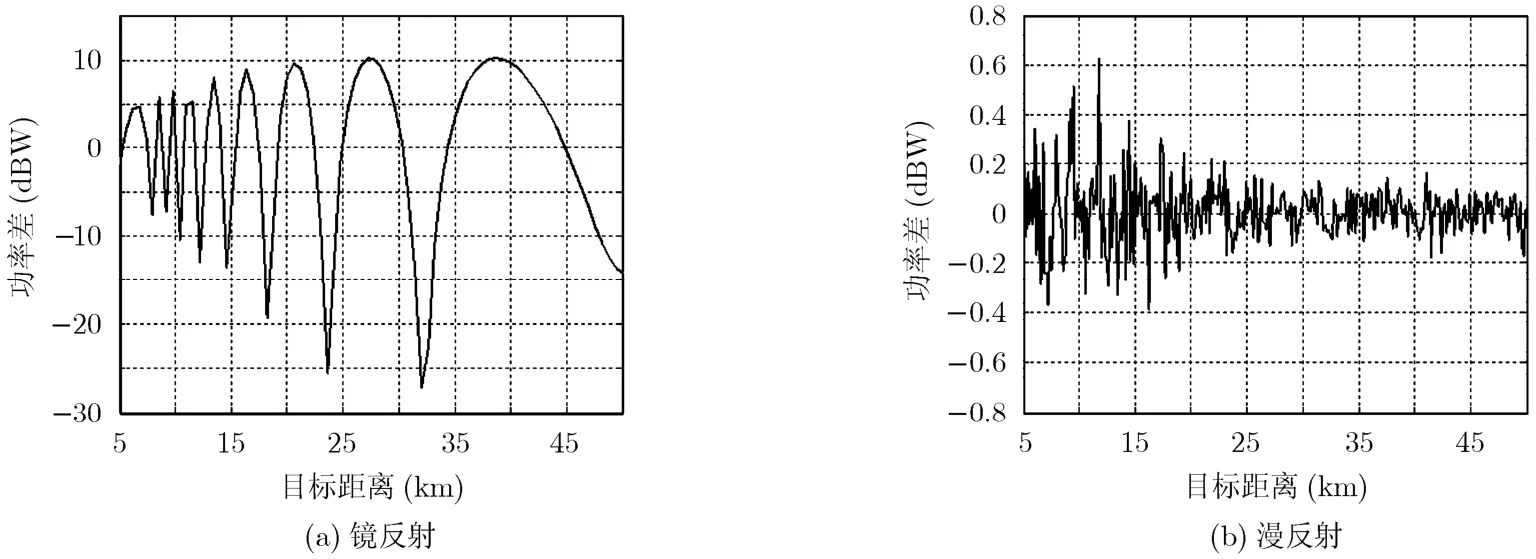
图4 多径导致的雷达接收信号功率起伏

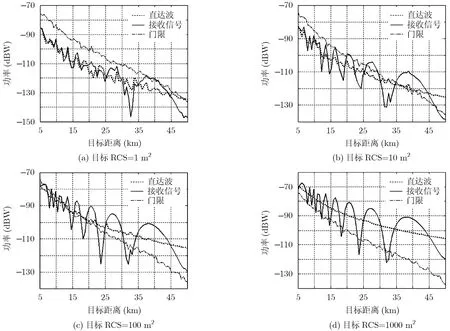
图5 多径、海杂波环境下雷达导引头接收信号

图5给出了多径条件下雷达接收信号图。图中，虚线表示直达波功率随目标距离的变化曲线，实线为多径条件下的雷达接收信号功率随目标距离的变化曲线，点画线为CFAR检测门限。从图5中雷达接收信号功率随目标距离变化的平滑度可以看出：当目标RCS=1 m2时，海杂波功率与目标回波功率相当，而对于RCS大于10 m2的目标，海杂波功率相对目标回波功率较小，雷达接收信号以目标回波为主。对于RCS=1 m2的目标，虽然多径散射对其回波有一定增强作用，但由于其RCS过小，回波功率仍低于检测门限；对于目标RCS=10 m2的情况，直达波信号功率在5-38 km距离段低于检测门限，在38-50 km距离段高于门限；受镜反射影响，雷达接收信号功率出现较大起伏。多径导致目标回波信号在22-25 km, 30-35 km, 45-50 km等距离段衰减，使得在26-29 km, 35-38 km距离段的目标信号增强，从而使得在该距离段无法检测的目标变得可检测。从图5(b)还可以发现：对于检测RCS=10 m2的目标，雷达导引头在50 km处开机，此时，雷达导引头处于目标回波的衰减区，回波功率低于门限，可见，雷达导引头过早开机，不一定会使其过早的检测到目标，而过早开机增加了其被发现的概率，因此，在选择开机时间时，要充分考虑多径散射的影响效果。当目标RCS=100 m2时，在15-50 km距离段，直达波功率高于门限，如图5(c)所示，但受镜反射影响，导致雷达导引头接收信号在17.6-19.2 km, 22.5-25 km, 31.8-33.6 km等距离段被衰减，回波功率低于门限，目标无法检测。对RCS=1000 m2的目标，在整个距离段，直达波信号功率均高于门限，受镜反射影响，雷达导引头接收信号在17.9-18.6 km, 23.2-24.2 km, 31.5-33 km等距离段被衰减，导致目标无法检测。因此，低掠射角情况下，雷达导引头检测RCS低于1 m2的目标时，海杂波强度对雷达导引头的检测性能起主导作用，雷达导引头检测RCS高于10 m2的目标时，多径效应对雷达导引头的检测性能起主导作用。多径效应对雷达导引头检测目标可能产生不利影响，也可能产生有利影响，影响效果视具体目标而定。

通过1000次蒙特卡洛仿真实验，分别得到了多径和海杂波条件下雷达导引头检测不同大小目标的检测概率，如图6所示。

考虑多径散射，目标回波信号为目标直达波、镜反射回波二者叠加时的雷达导引头检测概率如图6中实线所示。为了说明多径散射对雷达导引头检测性能的影响，图6中给出了目标回波信号仅考虑目标直达波时的雷达导引头检测概率，如图6中虚线所示。从图中可以看出：对于RCS=1 m2的小目标，多径效应对雷达导引头检测性能的提高或降低效果并不明显，且雷达导引头对该小目标在远距离目标具有一定检测能力，而在近程丧失了对该小目标的检测能力，这是由于随着目标距离的缩短，目标所在距离单元对应的电波入射角增大，导致海面散射系数增大，从而导致杂波信号增强，检测门限提高；对于RCS=10 m2的目标，多径效应降低了雷达导引头开机时刻的检测性能，但提高了雷达导引头在一些中距离段的检测性能；对于RCS=100 m2的目标，多径效应降低了雷达导引头在中距离段的检测性能，提高了雷达导引头在一些近距离段的检测性能；对于RCS=1000 m2的目标，多径效应降低了雷达导引头在中距离段和近距离段的检测性能。由图6可以推测：随着目标RCS的增加，目标可检测的距离段将逐渐增加，对于RCS超过104m2量级的大型舰船，被多径散射衰减的回波功率仍将高于检测门限，多径效应不会影响雷达导引头的检测性能。

5 结论

低空雷达导引头检测海面目标的性能受多径散射和海杂波影响明显。深入研究多径散射机理和海杂波特性为分析低空雷达导引头检测海面目标的性能提供了理论基础。本文对多径散射的镜反射、漫反射机理进行了分析，通过推导建立了多径散射镜反射和漫反射模型。与此同时，对低空雷达导引头所面临的海杂波环境进行了分析建模。在此基础上，综合考虑多径和海杂波环境，仿真分析了低空雷达导引头对海面不同大小目标的检测性能。结果表明：海杂波和多径散射对雷达导引头的检测性能的影响效果明显，影响效果随目标RCS的变化而变化。综合分析多径散射和海杂波对雷达导引头检测性能的影响为掠海飞行反舰导弹雷达导引头检测方法设计和性能评估提供了理论支撑。

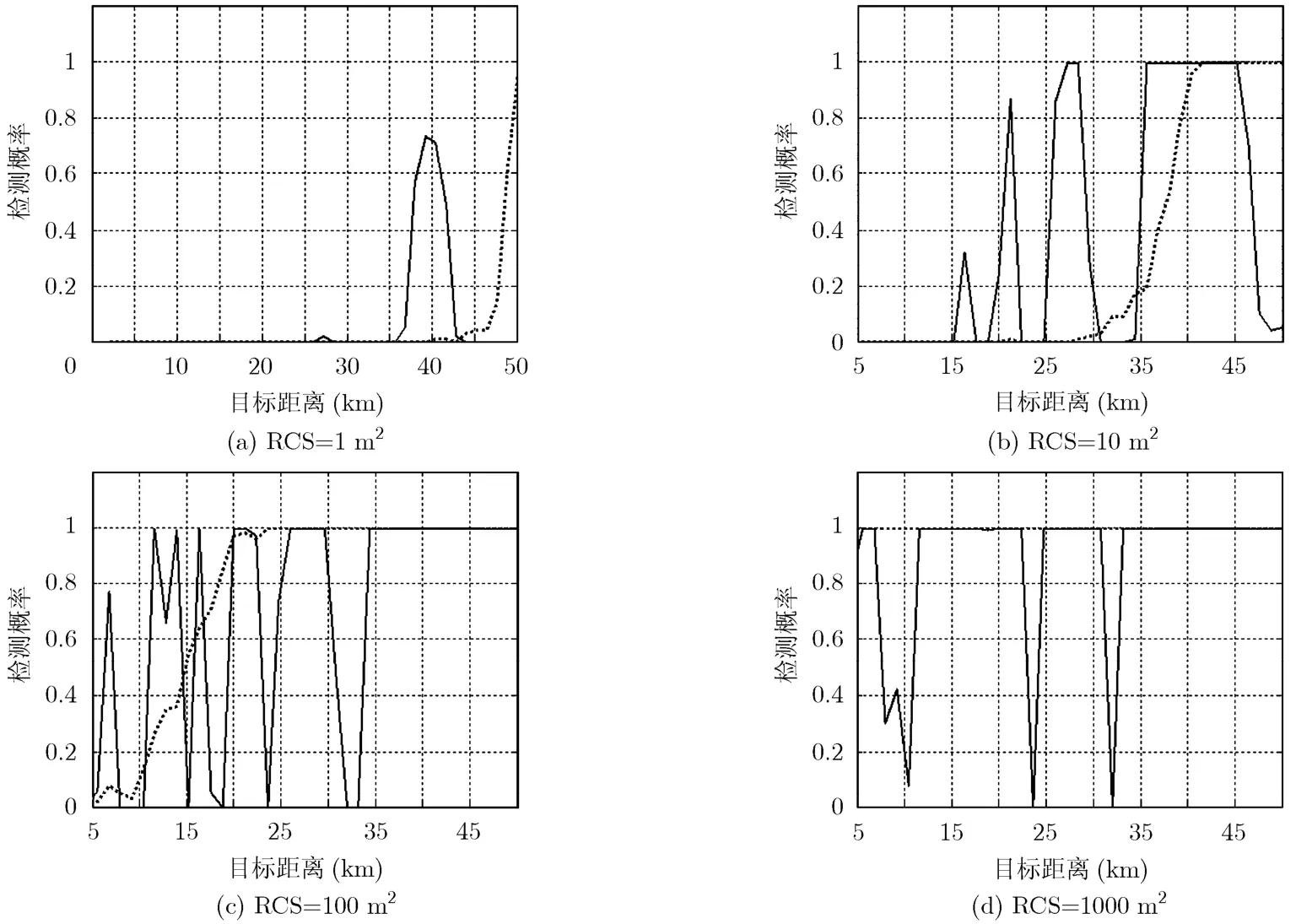
图6 多径、海杂波条件下不同大小目标的检测概率

[1] Sajjad N, Khenchaf A, and Coatanhay A. Electromagnetic wave scattering from ocean surface at low grazing angles[C].The 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009, Vol. 1: 196-199.

[2] Lamont-Smith T, Mitomi M, Kawomura T, et al..Electromagnetic scattering from wind blown waves and ripples modulated by longer waves under laboratory conditions[J]. IET Radar Sonar and Navigation, 2010, 4(2):265-279.

[3] Hansen V G and Mital R. An empirical sea clutter model for low grazing angle[C]. The 2009 IEEE Radar Conference,Pasadena, CA, United States, 2009, Vol. 1: 1-5.

[4] Greco M, Stinco P, and Gini F. Identification and analysis of sea clutter spikes[J]. IET Radar Sonar and Navigation, 2010,4(2): 239-250.

[5] Posner F L. Spiky sea clutter at high range resolutions and very low grazing angles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 58-73.

[6] Carretero-Moya J, Gismero-Menoyo J, Blanco-del-Campo A,and Asensio-Lopez A. Statistical analysis of a high-resolution sea clutter database[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2024-2037.

[7] Farshchian M and Posner F L. The Pareto distribution for low grazing angle and high resolution X-band sea clutter[C].The 2010 IEEE International Radar Conference, Washington DC, United States, 2010, Vol. 1: 789-793.

[8] Ahn Soyeon, Yang Eunjung, Chun Joohwan, et al.. Low angle tracking using iterative multipath cancellation in sea clutter environment[C]. The 2010 IEEE International Radar Conference, Washington DC, United States, 2010, Vol. 1:1156-1160.

[9] Ogden George, Matzner Shari, Zurk Lisa M, et al.. Multipath return for radar targets over a rough surface[C]. The 2007 IEEE International Antenna and Propagation Symposium,Honolulu, HI, United States, 2007, Vol.1: 4825-4828.

[10] Sinha A, Bar-shalom Y, Blair W D, et al.. Radar measurement extraction in the presence of sea-surface multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 550-567.

[11] Blair W D and Brandt-Pearce M. Statistics of monopulse measurements of Rayleigh targets in the presence of specular and diffuse multipath[C]. The 2001 IEEE International Radar Conference, Atlanta, GA, United States, 2001, Vol. 1:369-375.

[12] Daeipour E, Blair W D, and Bar-shalom Y. Bias compensation and tracking with monopulse radars in the presence of multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 863-882.

[13] Barton D K. Low-angle radar tracking[J]. Proceedings of the IEEE, 1974, 62(6): 687-704.

[14] Wilson S L and Carlson B D. Radar detection in multipath[J].IEE Proceedings of Radar, Sonar and Navigation, 1999,146(1): 45-54.

[15] Bucco Domenic and Hu Yi-ding. A comparative assessment of various multipath models for use in missile simulation studies[C]. AIAA Modeling and Simulation Technologies Conference, Denver, United States, 2000, Vol. 1: 1-10.

[16] 宋海娜, 胡卫东, 郁文贤, 等. 低入射余角下雷达海杂波的建模与仿真[J]. 国防科技大学学报, 2000, 22(3): 29-33.Song Hai-na, Hu Wei-dong, Yu Wen-xian, et al.. Modeling and simulation of low grazing angle radar sea clutter[J].Journal of National University of Defense Technology, 2000,22(3): 29-33.