供应链超网络均衡模型

董 琼, 马 军

(1.上海理工大学超网络研究中心,上海 200093;2.纽约州立大学奥斯威戈分校 商学院,奥斯威戈NY 13126;3.大连理工大学管理学院,大连 116024;4.沈阳工业大学管理学院,沈阳 110870)

近20年来,供应链网络的研究已经成为一个重要的研究领域,引起了理论界和企业界广泛的关注.供应链网络是产品从供应商到顾客的生产和运输过程中组织、人员、活动、信息和其它资源组成的一个协调的系统.供应链的任务是把原材料和零部件转换为成品,运送到最终顾客的手中.供应链管理涉及计划、执行、控制和运作管理,目的是满足顾客的需要和提高物料流通的效率.当今,先进的信息系统已经能够协调连接全球资源和全球市场的范围较大的和复杂的供应链网络.这促使运作管理的研究者能够提供一个更加广泛地和有效地的理论来理解这个复杂的系统,以及对这种问题的解决方法.因此,近年来,大部分供应链管理研究的文献[1]主要研究集中在概念本质的研究[2-5]和分析上[6-10].

目前大部分供应链管理研究方面的文献都集中在供应链内的问题上.例如,供应商的选择、网络分布设计、生产协调和库存管理.集中在供应链系统的特定部分,并且是针对子网的局部利益提供解决方法.这个子网通常范围有限,结构简单.例如,协调两层的一个供应商和两个零售商形成的单链.具有特殊和简单网络结构的供应链问题,可以通过构建优化模型来表示,通过假设特定的成本函数和需求分布函数,能够找到这些问题的解决方法.具有特殊和简单网络结构供应链的典型问题研究的缺点是应用范围有限,缺乏供应链网络研究的全球视角.文献[11-13]对这个方向已有的研究提供了较为全面的综述.

相对于这些微观的模型,一些新的研究成果试图从一个宏观的视角,给出供应链中各参与者之间关系全面的理解.这些研究提供了一个更加一般化的网络模型.它们由3层或者更多层组成,每层参与者的数量没有限制.这些研究的模型通常允许分散化决策、以及供应链内商家之间和供应链之间的竞争.本文将在Zhang等[14]的基础上针对这些模型及其实际应用研究作有限综述.

综述了基本的供应链模型,主要是3种基本模型,供应链网络参与者各自独特的分散化决策行为模型结构,及其导致供应链网络的外部效应;讨论了这3种基本模型的特点和局限性;总结了一个基本模型[15]在多目标决策、风险管理以及不确定需求市场条件下的多个扩展模型;针对模型的特殊应用进行了综述;总结了供应链网络风险及鲁棒性评估的研究.

1 基本模型

总结了供应链网络分散化决策的3个基本模型.第一个基本模型是由Nagurney等[15]撰写的最早涉及供应链网络均衡模型的文献.随后一系列的模型的扩展和本文引用的许多文献都是在此基础上进行的研究.第二个基本模型是由 Corbett等[16]2001年提出的独立线性装配链模型,随后,在2005年Carr等[17]进一步完善了该模型.第三个基本模型是Zhang等[18]2006年提出的供应链经济模型.

1.1 供应链网络均衡模型

Nagurney等[15]在2002年提出了第一个供应链网络的超网络经济模型.该模型将生产网络、销售网络,及运输网络的不同要素综合一体(见图1).该模型由生产商、零售商和消费市场三层组成.(见下页图2)生产商、零售商和消费市场在数量上没有限制.生产商依据生产成本和交易成本来决定生产量水平和针对每个零售商的运输数量.供应链的价格作为内生变量.该模型假设生产商追求利润最大化,并通过对生产和运输的模式决策来实现利润最大化.其次,零售商必须和生产商就运输量达成一致,并在消费者愿意支付的价格的基础上最大化其利润.零售商和消费市场之间的零售价格也作为内生变量.消费市场假设是弹性的与零售价格相关.除了零售价格,消费者还考虑交易成本.例如,从市场上获得产品的运输成本.消费者依据不同零售商的零售价格和交易成本来决策最优化的消费水平.

图1 供应链立体超网络结构示意图Fig.1 Supply chain supernetworks illustration

针对每个生产商、零售商和消费市场,最优化的条件是容易表述的.供应链网络均衡的定义是在不同层生产商、零售商和消费市场产品的交易成功的基础上,产品的流量和价格满足每层的优化条件的一种状态.该均衡问题在一定的条件下能够通过变分不等式整合所有的优化条件来给出一个解.每个生产商的内部价格和每个零售商的零售价格都可以从该模型中得以求解.该文献还阐述了在唯一供应链网络均衡存在时,生产成本、交易成本、处理成本和需求函数的条件.

Nagurney等[15]给出了由利润最大化决策者组成的多层网络,每层的决策者的数量不限,生产成本函数和交易函数更为普遍的供应链均衡模型的结构.该结构在不同方向上修正和扩展了该领域的研究.

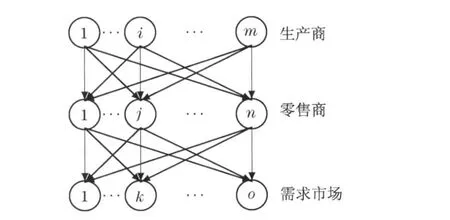
图2 三层供应链网络示意图Fig.2 3-Tier supply chain network

1.2 独立线性装配链模型

Corbett等[16]2001年提出了确定性需求条件下的连续性供应链网络中的先进入者和后进入者竞争的详细模型.该模型中的网络包括两层,零部件制造的上游层和产品装配的下游层.模型针对所有下游厂商假设独立线性反需求函数和独立的生产成本函数,针对所有的上游厂商假定独立的线性供应价格.通过采用特殊结构的成本函数和需求函数,该文献给出了一个解的近似形式,可以用于供应链网络的定量分析.特别是,在进入阶段构建同时博弈模型,该阶段参与者考虑后进入者竞争(古诺模型)结果的基础上制定进入决策.价格和生产数量的近似表达式可以通过每层参与者数量函数衍生而来.该文还就以下的问题作了研究,并得出一些有趣的结论.任何一层固定和变动成本对其它层价格、数量和利润的影响是什么?在供应链中,“买方优势”和“供应方优势”对于邻近层和非邻近层的价格、数量和利润的影响是什么?额外的下游和上游的进入者的边际效应是什么?任何一层的合作与另一层的竞争的关系是什么?上游和下游厂商的合作对于厂商的竞争优势的影响是什么?每一层有多少个参与者能够存活?参与者的这些组合中哪个能够反映均衡状态?终端市场对于需求的反应如何被上游层所接收?如果需求曲线或者生产成本函数或者进入者发生改变,每层参与者的数量如何变化?竖向整合和不整合的结构如何比较?是否存在这样唯一的和收敛的结构,该结构是具有固定成本和变动成本的一个系统?

该文献阐述了供应链结构的可行性和稳定性,并且通过晶格参数展示了在进入纯策略博弈中,总是有均衡的结构.总的来说,该文献分析了许多有趣的问题,得出了具有特殊显性成本和需求函数的两层供应链网络定性的性质.这些发现的经济意义是很有价值的,但是假设所有公司具有相同的成本和需求函数是不现实的.

在Corbett等[16]研究基础上,Carr等[17]2005年提出了多层次装配结构供应链网络.在这个装配网络中,厂商合作进入同质节点,主要包括具有相同产品(零部件)生产特征(包括能力和成本函数)的相同的厂商.每个节点采用多个零件和部件生产产品,这些零部件由不同的节点供应.任一节点的生产流程是按照固定比例依据订单的纯装配生产过程.竞争是通过“连续合作古诺模型”来实现的,在模型中厂商在给定所有输入产品和互补产品价格的基础上,依据利润最大化原则,决策针对下游市场的生产数量.供应相同后续节点的前节点生产数量通过价格机制进行协调,从而以合适的比例来生产互补产品.与Corbett等[16]研究相似的是终端产品的需求函数假定是线性的,所用节点的生产成本也是线性的.在这些假设前提下,多层次装配网络的均衡价格可以通过一组线性方程组给出.在Corbett等[16]研究基础上,对于单装配线和多支线的两阶段子系统,给出了均衡数量和均衡价格近似形式的表达式.该文献进一步分析了任何一个装配结构都能被转换成等价的结构,该结构中任一节点装配的零部件不超过两个.因此,大结构问题可以通过特定的线性方程来直接解决,或者通过迭代成为小结构问题来解决.

该文献的模型是Corbett等[16]模型从两层到多层,从纯生产到装配结构的扩展.针对所有的需求和生产成本函数依然继承了线性的假设,并且对于所有参与厂商假设是连续古诺垄断决策.该模型还假设每个上游厂商仅能供应一个下游厂商,但每个下游厂商可以从多个上游厂商进行购买.这个假设也限制了模型更广泛的应用,因为更多实际的供应链是一个供应商拥有多个消费者.

1.3 供应链经济模型

Zhang[18]2006年提出的供应链经济网络模型,阐述了供应链的形式和供应链之间竞争的形式.该文献提出了供应链经济和市场相关链的概念.供应链经济定义为涉及一个或多个互相关联的产品或服务,由企业组成的联盟,协调进行采购、生产、分配、销售和消费相关活动的网络.供应链经济被认为是相关多个或多重供应链组成的网络.市场相关链是与特定消费市场相关的供应链的子网.我们考虑一个利益最大化的商业环境,其中有多个代表供应链中的不同阶层的企业,由原材料供应商、生产商、物流厂商、经销商、批发商和零售商组成.这些企业在这样的竞争环境里,基于本身所在的行业及自身的竞争条件,决定进入或不进入供应链经济.

该模型具有以下的特色:

这是针对供应链与供应链竞争研究的第一个定量模型.它可以用于计算供应链赢家的市场份额.模型中供应链的形式及其最优供应链网络结构,在供应链经济中流量的确定过程中得以给出.

a.运作边和交互边 网络模型由运作边和交互边组成,这些边分别承载物料流和信息流.运作边代表供应链网络中企业的相关运行.交互边代表的企业与企业交易关系,其上的函数用于测量供应链运作协调和整合的效果.

b.多市场 多市场包括不同的地理区域,同时也可以包括电子商务.

c.总成本函数 在不同层的运行中,并没有强加人为的假设条件.模型的主要结论在非线性函数和不可分成本函数下是有效地,但是在特殊的函数条件下,例如线性成本函数,就能表示的更加清晰.

d.多产品异质链 对由多个相关却不同性质产品及服务的异质供应链该模型给出了一个般的结构,这是供应链竞争研究模型最基本的突破.其他相关研究,例如Nagurney等[15],Corbett等[16],Carr等[17]都是建立在单一产品并具有相同结构链的基础上的.

e.一般结构链 这是针对一般的、任意结构的供应链分析的第一个模型.该供应链能够根据分析问题的需要,可以任意的设定相应的层次数.而不是像目前大部分研究限于固定的层次和节点数(例如Nagurney等[15]、Cachon等[19-21]).另外,模型中不同层可以用不同函数来表示,不需要限定特定的类型,例如Corbett等[16]和Carr等[17]的产品装配类型.

对比Carr等[17]的连续古诺决策模型,该模型源于微观经济的空间价格均衡模型(Samuelson[22]、Takayama等[23]).因为供应链的边际成本不仅依靠自身物料流,而且依靠其他相关供应链的物料流,所以模型可以通过运输用户均衡的独立流量最短路径方法[24]来实现,并形成变分不等式问题来求解.

2 扩展模型

在这一部分主要综述Nagurney等[15]的基本供应链网络均衡模型的多个扩展模型.这些扩展模型主要包括多目标决策者、随机需求市场、供应商的风险管理、结合电子商务和供应链的全球视角等方向.所有的这些研究都是在基本的供应链模型基础上对于现实问题更深入的理解和描述.

Nagurney等[25]把B2B和B2C电子商务类型整合到供应链网络均衡模型的超网络中.模型中,不仅考虑到交通网络,生产网络,销售网络,还融入了互联网在供应链中的影响.生产商不仅能够销售和运输产品给零售商,而且能够通过网络直接销售和运输给顾客.另外,还可以通过电子商务与零售商交易.随着电子商务的增加,生产商和零售商面临着一个简单利润最大化的问题,并且可以得到最优化的条件.消费者对比生产商和零售商的价格,并在交易成本的基础上做出消费决策.该模型是在供应链网络均衡模型基础上针对电子商务方向的一个扩展.具有相同的决策者层,即生产商、零售商和消费者.与供应链网络均衡模型相似的是都转化成变分不等式问题求解.调整的部分是用投影动态系统研究非均衡决策者行为与网络均衡点相一致的平衡状态.并用实例提供和计算了生产、运输和消费者购买的均衡解.

在供应链网络中分散化决策的代理商在决策时经常面临不止一个目标.生产商不仅想提高销售利润,而且还希望能够扩大市场份额.零售商要考虑到利润、运输时间和消费者服务水平.不同层的消费者在个体行为下主要权衡获取产品的时间和成本.

Nagurney等[26]提出了在空间上分布在不同区域的供应和生产同种产品的多目标生产者和多层次多目标消费者的空间经济网络.每个生产者能够在不同的市场生产和销售产品,依据成本的不同选择不同的运输方式.生产者具有两个决策目标,也就是在决策最优化生产水平和针对市场的运输模式下的最大化利润和最大化市场份额.消费者根据不同的特征归类为不同的类别,例如:地理位置、消费行为、出行模式和收入水平.消费者依据产品的价格、与获得产品相关的运输时间和运输成本来决策在每个市场采购的数量.不同类型的消费者在个体决策行为下权衡获得产品相关的时间和成本.模型源自空间价格均衡问题,然后形成变分不等式来求解最佳生产水平、所有生产者的运输模式和不同类型消费者的最优购买数量和分布.

Dong等[27]扩展了Nagurney等[26]模型.并且把多目标决策引进基础的三层供应链网络均衡模型.在本文中,和Nagurney等[26]的模型相同,生产商具有相同的决策目标,消费者的类型也是相同的.额外增加一层多目标决策者是零售商,具有3个决策目标:利润最优化、运输时间最小化和服务水平最佳化.每个零售商依据不同的行为权衡这几个决策目标.运输的方式的特征由特定运输成本和运输时间函数来表示.因此,特殊运输选择可能是较少的运输时间,但是运输成本较高,或者相反具有较长的运输时间和较低的运输价格.零售商要求支付高的价格可能是运输更快,相反,如果选择一个慢的、便宜的运输模式,生产商可能会接受一个更低的价格.服务水平表明产品一定时间内没有脱销的概率.通常高的服务水平表明较高的平均库存水平,能够满足数量较大并且较频繁的订单.因此,每个零售商设定的服务水平表明了他的储存成本、运输时间和成本.

该文献建立了生产商、零售商和消费者在非合作条件下达到多目标最优化状态的均衡条件(纳什均衡).

对供应链管理的挑战源于最终市场的不确定性.一个市场消费者的需求通常是一个随机变量,不仅受零售商价格的影响,而且受竞争者价格的影响.除了需求的不确定性,供应链代理商还需要控制供应链风险,例如原材料价格的变化、供应短缺、运输问题、生产中断和机器故障等.以下的文献主要从风险管理和需求的不确定性方面研究供应链竞争的网络均衡模型.

Mahajan等[28]提出了零售商面临不确定性需求市场的两层模型.该模型在假定产品价格是外生给定的前提下,研究零售商之间的库存竞争问题.从建模的观点来看,它提出了库存变量,但忽略了市场价格变量.

Dong等[29]提出三层供应链网络模型,需求是不确定的和零售折扣相关.作为供应链网络均衡模型的扩展,该模型构建了相同拓扑结构的网络来研究顶层生产商之间的竞争和中间层零售商之间的竞争,但是零售商和消费市场之间的运输时间是不确定的.零售商对于额外的供应与需求和库存与短缺分别采用特殊的折扣来处理.该模型通过变分不等式问题给出了所用利润驱动的决策者达到均衡状态的条件.均衡状态是存在的和唯一的,转换成变分不等式的函数是建立在收敛基础上的.

Dong等[30]在该研究中没有显性地表达库存变量的使用,但是在不同层相关代理商之间提出了竞争的观点,以及以动态价格来反映竞争和不确定性市场需求.

Dong等[31]把多目标决策引入了具有不确定性需求的供应链网络中,整合了Dong等[27]和Dong等[30]的研究,在整体均衡结构下,第一次结合多目标决策和不确定性决策提出供应链网络模型.除了整合这两个模型之外,还扩展了Dong等[27]和Dong等[30]模型的层次,增加了生产商供应产品给分销商,零售商从分销商订购产品,然后在消费市场上销售.生产商和零售商的决策目标和Dong等[27]的研究是相同的.分销商决策目标是从每个生产商获得“最优”产品的数量、“最经济”的运输模式和“最优”服务水平.

Nagurney等[32]整合供应风险和电子商务到Dong等[31]的模型中,在模型中考虑到供应方生产商和分销商的风险管理,同时测量需求方风险.因为零售商可能是实体或者非实体,所以模型允许在生产商和零售商之间,分销商和零售商之间进行电子商务形式的电子交易.

Nagurney等[33]考虑到风险和不确定性,提出全球供应链网络经济的动态模型.此外,供应方风险以每个生产商和分销商的多目标决策问题来表示(不同的目标不同的权重),需求方风险以不确定性需求来处理.

Nagurney等[34]第一次提出供应链网络中所有决策者的非均衡行为的调整过程是通过投影动态系统来解决.Nagurney等[35]采用超网络模型权衡在运输和通讯网络中决策.

Nagurney等[36]构建了全球供应链网络模型,生产商、分销商和零售商可以是相同或者不同的国家,也可以通过不同货币进行交易.生产商和分销商是多目标决策者,追求利润最大化和风险最小化.零售商面临不确定性产品需求.该文献给出了均衡状态的条件,并建立了有限维度的变分不等式.

3 应 用

3.1 电力供应链网络

美国和其它国家的电力产业正在经历管理和运行的改变.这种改变的思路是从一个垂直整合性垄断产业的集中管理方法向开放和竞争的环境转变.竞争市场的出现和市场参与者数量的增加,不仅根本上改变了电力交易的模式,而且改变了电力供应链的结构.这些新的结构需要新的数学模型、工程模型和算法工具来表示.此外,发电燃料的可靠性在经济价值和国家安全方面也是一个重要议题.

然而,极度依靠矿物燃料转换成电能已经对环境产生了巨大的影响.例如美国二氧化碳和一氧化氮的排放,目前三分之一以上来自于电力.在中国,目前电力部门占用的三分之一以上的煤炭的消费,导致了75%空气污染.随着全球变暖证据的增加,任何能够减缓不稳定气候带来巨大风险的政策,都必须考虑到电力产业[37].

本文综述的文献都是运用供应链网络模型来分析电力网络的问题,包括电力生产、电力供应、电力的传输和消费,也包括污染税和排放控制等.

Nagurney等[38]针对电力生产、供应、运输和消费,提出了第一个供应链网络模型.该模型和供应链网络均衡模型有相似的网络结构,顶层的生产商由电厂代替,中间层的零售商由电力供应部门代替,需求市场在最底层.在模型中分散化的决策者包括电厂、电力供应部门、运输部门以及与需求市场相关的消费者.

最佳条件可由电厂和电力供应部门的一阶条件获得,市场均衡条件作为需求市场互补的不等式,然后,转化为变分不等式,从而可得供应链网络不同层之间的均衡电力流量和节点的价格.

Wu等[39]针对环境问题,在Nagurney等[38]模型的基础上提出了几个扩展模型.全球环境的变化和能源安全都鼓励国家和地区采取污染税/碳排放税.政策干预最主要的部分是根据电厂使用的燃料的类型直接在电力行业征收不同的税收.考虑到污染税,该模型整合了电厂的期权投资组合行为后,构建了电力供应链网络.该文献形成了具有弹性需求的运输网络均衡模型,进行了定性的分析和求解.并通过多个示例阐述了污染税/碳排放税的变化是如何影响均衡的电力供应链网络生产的输出量,需求市场价格和碳排放总量.

Matsypura等[40]把 Nagurney等[33]和Nagurney等[38]的模型作为基础,形成了具有直接供应层的总的电力供应链网络模型,该模型引入了可再生能源和不可再生能源的供应商,及其最优化的行为.网络运输不同流量不同类型的燃料,该燃料在处理非可再生能源的电厂转化成电能.该扩展模型陈述了燃料可能来自不同地点的可能性,存在与运输和生产相关的成本,生产可以使用不同类型的燃料或者使用不同类型燃料的组合产生电能.

针对不同的决策者,形成了最优化的条件,包括燃料供应商、电厂、电力供应商、运输服务提供商和需求市场的消费者,并建立了满足有限维度变分不等式问题的均衡条件.

Nagurney等[41]构建了具有已知需求的静态电力供应链网络均衡模型,建立了与具有固定需求超网络结构的运输网络均衡模型的等价关系.这种等价关系表明需求随着时间变化的动态电力供应链网络模型可以通过进化变分不等式来表达.该文献阐述了多个动态电力供应链网络问题是如何通过进化变分不等式和投影动态系统联合的理论来解决的[42].

Nagurney等[43]在电力供应链网络方面针对电厂构建了最优碳排放税应用的模型.环境的改变和能源的安全直接导致国家和地区采用征收碳排放税干预电厂运作.该模型允许针对不同的环境政策使用三种不同类型的碳排放税,即第一个是完全分散化的计划,税收被用于每个个体电厂从而确保不会超过每个已分配的排放范围;第二个是集中的计划,针对整体的电力供应链网络在碳排放总量方面假设固定的范围;第三个是允许这个范围是税收的函数.通过多个示例计算最优碳排放税、均衡的电力流量和需求量.

Liu等[44]最近的研究构建了包括燃料市场的电力供应链网络的新模型,该模型考虑到了经济交易网络和运输网络.该模型运用案例分析法,分析了新英格兰地区的6个州,5种类型的燃料,82个部门共计583个电厂和10个需求市场.案例阐述了通过模型可以很好地预测新英格兰地区的区域电力价格.运用敏感性分析,分析了燃料价格的变化对电力价格的影响.此外,该文献还通过电力网络和电力市场分析了汽油价格对天然气价格的显著影响.

以上模型仅适用于没有电力管制规定的国家和地区,不适用于其电力的生产和分配都由国家集中管理的国家和地区.当然,通过构建类似的集中优化问题网络来研究国家整体电力供应网络,也将是一个有趣和可行的研究.

3.2 金融和社会供应链网络

金融和社会网络问题也可以从供应链网络模型角度考虑.以下的4篇文章整合了金融工程、关系价值和社会责任于供应链网络之中.

Nagurney等[45]构建了具有金融企业、中间商和需求市场的金融网络供应链均衡模型.其中,金融企业是双目标决策者,追求净收入最大化和风险最小化.模型中同层竞争不同层合作.模型采用不同的权重和普通的风险函数,统一的基准来比较目前的价格和资金流量.通过变分不等式问题达成均衡条件.同时提出一种算法,把变分不等式问题分解成简单的网络子问题,每一个都可以得出解析式的解.

Cruz等[46]提出涉及金融工程方法的带有社会网络的整体全球供应链网络动态模型.研究了在电子商务环境下的社会网络中的不同生产商、零售商和消费者的多目标决策行为.决策者的多目标包括:利润最大化、关系价值最大化和风险最小化.模型假设互相之间的关系水平影响交易的成本和风险,并且在决策者的效用函数中得以表示.该文献探究了涉及产品价格和关系水平的全球产品交易在达到了均衡状态的动态联合演化过程.价格机制保证了在多级、多层的金融工程超网络中每个决策者能够达到最优.

Cruz[47]研究了具有环境保护社会责任的供应链网络.该模型和Cruz等[46]模型的结构相似,具有多目标的决策代理,追求利润最大化、排放(污染)最小化和风险最小化.该模型采用了与价格与社会责任活动水平相关的动态产品流量.

Hsueh等[48]采用三层供应链网络,包括生产商、分销商和零售商.研究了3种不同模式下供应链代理商的行为和收益,3种模式包括:分散决策供应链网络、集权决策供应链网络和考虑社会责任的供应链网络.并证明了在集权决策供应链网络中,在代理商之间假设没有竞争,系统最优解通常是不存在的或者是不稳定的,因为每个成员总是追求自身利益最大化.该文献还探讨了所有生产商考虑社会责任的分散化供应链网络的均衡解.提出了在生产商之间的协调策略.生产商能够量化支出和社会责任活动收益,同时和集权供应链一样能够促使分散化供应链的执行.并通过多个示例测试具有超网络特征的混合对角化方法,结果显示在决策中考虑社会责任,无论供应链网络是否协调,整个供应链网络的总体利润能够得到提升.

上述的模型对金融和社会供应链网络问题作了初步的研究.但一些主要问题还有待更多研究,比如,变量的权重和普遍的风险函数不能完全表示应用问题的特殊性,关系价值在现实中是主观的,难以测量的.

3.3 逆向物流

Nagurney等[49]构建了针对电子废物逆向供应链管理的供应链网络均衡模型.四层网络结构,分散化决策者是电子垃圾的源头、废物收购者、废物处理者和不同产品的需求市场.模型的中间层企业之间横向竞争,不同层企业之间竖向合作.其特性在于允许电子废物流沿着回收网络转换成其它产品(或者副产品).并采用变分不等式求解均衡物料流和供应商的最优价格.

Hammond等[50]构建了供应链均衡模型来研究闭环的供应链网络.生产商生产同种产品在消费市场上销售.产品由新的原材料和顾客返回的产品再加工的材料构成.通过从生产商到顾客市场的零部件装配、半成品到成品的前向物料流和顾客返回产品拆卸成可再次使用的零部件返回到生产商的逆向物料流形成一个闭环.社会作为额外的参与者,主要关心系统的环境绩效.与Nagurney等[15]的模型类似,通过古诺-纳什博弈模型,从而形成变分不等式.该模型探究了欧盟指令在促使生产商针对电子垃圾形成闭环的效率.

以上两个逆向物流供应链网络模型是具有多代理商的古诺纳什结构,不同阶段逆向链上的企业是独立决策的参与者.可是,该模型没有考虑企业在运作中,特别是库存策略之间的协调问题.

4 供应链网络关键性能及鲁棒性

网络的关键性能效用及鲁棒性对网络设计、风险归避有着重要的作用.很多研究已给出了刻画网络性能及效用的一系列指标.然而,在供应链网络、交通网络中,不仅网络的拓扑结构对其性能和效用有影响,而且还有流量、需求量、费用等也对其关键性能有很大影响.同时,这样的网络问题,往往还要考虑多决策者竞争的因素.所以,一般图论中的性能指标无法很好地描述供应链网络的关键性能和效用.Zhu[51]等率先给出了一个描述有确定需求量的交通问题的效用指标.他们利用需求量加权的平均负效用值,来衡量交通网络的效用.这一指标已在实际的问题中得以运用.Nagurney等[52-53]随后定义的N-G指标具有更一般性.它适用于各种交通网络问题,无论是有确定需求,还是弹性需求,该指标都能很好地刻画网络的效用.N-G指标用在网络均衡状态下的需求与费用比的平均值来描述网络的效用.在此基础上,Nagurney和Qiang给出了网络鲁棒性的定义.依此,网络中各边、节点,或子网络的关键性也得以确认.

Nagurney等[54]提出了一个新的供应链超网络模型.该模型研究了各种不确定因素,包括来自供应商的不确定性,来自需求市场的不确定性,各种交通运输模式费用/时间的不确定性等.文章给出了在众多不确定因素下供应链网络的鲁棒性.

5 结 论

本文对供应链管理领域新的方向-供应链网络均衡模型进行了有限的综述.总结了最初的供应链网络均衡模型,以及不同的扩展模型.并总结了供应链网络均衡模型的一些应用,范围主要包括:电力供应、环境保护、金融工程、社会网络、逆向物流和回收再生、全球供应链管理和电子商务.在这些模型中采用的数学工具包括:变分不等式、投影动态系统、博弈论、多目标规划和随机过程.

本文综述最近的文献都是具有网络均衡模型特点的,目的是促进具有多层多代理商的分散化决策网络的研究.提到的文章提供了研究整体供应链的宏观视角.它们可以综合研究供应链中的物料流量、资金流量、信息流量和价格设定等.这些模型对相关政策研究,例如环境保护等外在因素对供应链影响,提供了很好的方法.这些模型的不足在于缺乏关注运作层面的微观视角,例如库存管理问题和基于全球视角的模型在现实问题中执行的困难.

进一步研究的方向主要有:a.现实世界供应链网络数学模型的案例分析;b.把微观运作问题整合到宏观模型中;c.整合纵向的库存协调问题到横向的竞争中;d.链内竞争.我们期待在这些已有的工作基础上,出现更多的供应链网络新成果.

[1] STADTLER H,KILGER C.Supply Chain Management and Advanced Planning[M].Berlin:Springer,2000.

[2] POIRIER C C.Supply Chain Optimization:Building a Total Business Network[M].San Francisco:Berrett-Kochler Publishers,1996.

[3] POIRIER C C.Advanced Supply Chain Management: How to Build a Sustained Competitive Advantage[M]. San Francisco:Berrett-Kochler Publishers,1999.

[4] MENTZER J T.Supply Chain M anagement[M]. Thousand Oaks:Sage,2000.

[5] BOVET D.Value Nets:Breaking the Supply Chain to Unlock Hidden Profits[M].New York:Wiley,2000.

[6] FEDERGRUEN A,ZIPKIN P.An inventory model with limited production capacity and uncertain demands I:The average cost criterion[J].Mathematics of Operations Research,1986,11:193-207.

[7] FEDERGRUEN A.Centralized planning models for multi-echelon inventorysystems underuncertainty [J].Handbooks in Operations Research and Management Science:Volume on Logistics of Production and Inventory,1993,4:133-173.

[8] SLATS P A,BHOLA B,EVERS J J,et al.Logistic chain modeling[J].European Journal of Operations Research,1995,(87):1-20.

[9] BRALEL J.SIMCHI-LEVI D.The Logic of Logistics:Theory[C]∥Algorithms and Applications for Logistics Management.New York:Springer,1997.

[10] HENSHER D,BUT TON K,BREWER S,et al. Handbook of Logistics and Supply Chain Management [M].Oxford:Elsevier,2001.

[11] GEOFFRION A M,POWER R F.Twenty years of strategic distribution system design:an evolution perspective[J].Interface,1995,25:105-127.

[12] BAZARAA M S,SHERALI H D,SHET TY C M. NonlinearProgramming:Theory and Algorithms [M].New York:John Wiley&Sons,1993.

[13] ERENGUC S S,SIMPOSOR N C,VAKHARIA A J. Integrated production/distribution planning in supply chains:An invited review[J].European Journal of Operations Research,1999(115):219-236.

[14] ZHANG D J,TENG D C.Recent advances in mathematical modeling of supply chain network equilibrium [Z].Advances in Mathematics and Its Applications, USTC Publishing House,2009,241-269.

[15] NAGU RNEY A,DONGJ,ZHANGD.Asupply chain network equilibrium model[J].Transportation Research E,2002,(38):281-303.

[16] CORBETT C,KARMARKAR U.Competition and structure in serial supply chains with deterministic demand[J].ManagementScience,2001,47(7): 966-978.

[17] CARR S,KARM ARKAR U.Competition in multiec-helon assembly supply chains[J].Management Science,2005,51(1):45-59.

[18] ZHANG D.A network economic model for supply chain versus supply chain competition[J].Omega:The International Journal of Management Science,2006, 34:283-295.

[19] CACHON G,ZIPKIN P.Competitive and cooperative inventory policies in a two stage supply chain[J]. M anagement Science,1999,45(7):936-953.

[20] CACHON G,LARIVIERE M.An equilibrium analysis of linear and proportional scare capacity[J].IIE Transactions,1999,31(9):835-850.

[21] CACHON G,LARIVIERE M.Capacity choice and allocation:strategic behavior and supply chain performance[J].M anagementScience,1999,45(8): 1091-1108.

[22] SAM UELSON P A.Spatial price equilibrium and linear programming[J].American Economic Review, 1952,42:283-303.

[23] TAKAYAM A T,JUDGE G G.Spatial and Temporal Price and Allocation M odels[M].Amsterdam:North Holland,1971.

[24] WARDROP J G.Some theoretical aspects of road traffic research[J].Proceedings of the Institute of Civil Engineering Part II,1952(3):325-362.

[25] NAGURNEY A,LOO J,DONG J,et al.Supply chain networks and electronic commerce:A theoretical perspective[J].Netnomics,2002,4:187-220.

[26] NAGURNEY A,ZHANG D,DONG J.Spatial economic networks with multicriteria producers and consumers:statics and dynamics[J].Annals of Regional Science,2002,36:79-105.

[27] DONG J,ZHANG D,NAGURNEY A.Supply chain networks with multicriteria decision-makers[C]∥TAYLOR M A P.Transportation and Traffic Theory in the 21st Century.Pergamon:2002:179-196.

[28] MAHAJAN S,RYZIN G V.Inventory competition under dynamic consumer choice[J].Operations Research,2001,49:646-657.

[29] DONG J,ZHANG D,NAGURNEY A.Asupply chain network equilibrium model with random demands[J].European Journal of Operational Research, 2004,156:194-212.

[30] DONG J,ZHANG D,NAGURNEY A.Asupply chain network equilibrium model with random demands[J].European Journal of Operational Research, 2004,156:194-212.

[31] DONG J,ZHANG D.YAN H,et al.Multitiered supply chain networks:multicriteria decision-making under uncertainty[J].Annals of Operations Research, 2005,135:155-178.

[32] NAGURNEY A,CRUZ J,DONG J,et al.Supply chain networks,electronic commerce,and supply side and demand side risk[J].European Journal of Operational Research,2005,164:120-142.

[33] NAGURNEY A,MATSYPURA D.Global supply chain network dynamics with multicriteria decisionmaking under risk and uncertainty[J].Transportation Research E,2005,41:585-612.

[34] NAGURNEY A,ZHANG D.Projected Dynamical Systems and Variational Inequalities with Applications[M].Norwell:KluwerAcademic Publishers Groups,1996.

[35] NAGURNEY A,DONG J.Supernetworks:decisionmaking for the Information age[M].Cheltenham: Edward Elgar Publishing,2002.

[36] NAGU RNEY A.CRUZ J,DONG J.Global supply chain networks and risk management:A multi-agent framework[C]∥CHAIB-DRAA B,M ULLER J P. Multiagent-Based Supply Chain Management.Berlin: Editors Springer,2006:103–134.

[37] NAGURNEY A,LIU Z,WOOLLEY T.Optimal endogenous carbon taxes forelectric powersupply chains with power plants[J].Mathematical and Computer M odelling,2006,44:899-916.

[38] NAGURNEY A,MATSYPURA D,A supply chain network perspective for electric power generation,supply, transmission,and consumption[C]∥KONTOGHIORGHES E J,GATU C.Optimisation,Econometric and Financial Analysis.Berlin:Springer,2006:3-27.

[39] NAGU RNEY,WU K A,LIU Z,et al.Modeling generator power plant portfolios and pollution taxes in electric power supply chain networks:a transportation network equilibrium transformation[J].Transportation Research D,2006,11:171-190.

[40] MATSYPURAL D.NAGURNEY A.LIU,Z.Modeling of electric power supply chain networks with fuel suppliers via variational inequalities[J].International Journal of Emerging Electric Power Systems,2007,8: 1-5.

[41] NAGU RNEY A,LIU Z,COJOCARU M,et al.Dynamic electric power supply chains and transportation networks:an evolutionary variational inequality formulation[J].Transportation Research E,2007,43: 624-646.

[42] COJOCARU M G,DANIELE P,NAGURNEY A. Projected dynamical systems and evolutionary variational inequalities via hilbert spaces with applications [J].Journal of Optimization Theory and Applications,2005,27:1-15.

[43] NAGURNEY A,LIU Z,WOOLLEY T.Optimal endogenous carbon taxes forelectric powersupply chains with power plants[J].Mathematical and Computer Modeling,2006,44:899-916.

[44] LIU Z A,NAGURNE Y.An Integrated Electric Power Supply Chain and Fuel Market Network Framework:Theoretical Modeling with Empirical Analysis for New England[Z].http∥:supernet.som.umass. edu,2007.

[45] NAGU RNEY A,KE K.Financial networks with intermediation:Risk management with variable weights [J].European Journal of Operational Research,2005, 172:40–63.

[46] CRUZ J,NAGURNEY A,WAKOLBINGER T.Financial engineering of the integration of global supply chain networks and social networks with risk management[J].Naval Research Logistics,2006,53:674 -696.

[47] CUUZ J.Dynamics of supply chain networks with corporate social responsibility through integrated environmental decision-making[J].European Journal of Operational Research,2008,184(3):1005-1031.

[48] HSUEH C.CHANG M.Equilibrium analysis and corporate social responsibility for supply chain integration[J].European Journal of Operational Research,2008,190(1):116-129.

[49] NAGURNEY A.TOYASAKI F.Reverse supply chain management and electronic waste recycling:A multitiered network equilibrium framework for e-cycling[J].Transportation Research E,2005,41:1-28.

[50] HAMMOND D,BEULLENS P.Modelling oligopolistic closed loop supply chains[C]∥Proceedings of 13th CIRP Life Cycle Engineering Conference,Sao Paolo:2006.

[51] ZHU D,HU Y,LI Y,et al.A new measure for airline networks performance evaluation and critical cities identication[Z].Shanghai:Fudan University,2006.

[52] NAGU RNEY A,QIANG Q.Fragile Networks:Identifying Vulnerabilities and Synergies in an Uncertain World[M].New York:JohnWiley &Sons, INC,2009.

[53] NAGURNEY A,QIANG Q.A network efficiency measure with application to critical infrastructure networks[J].Journal of Global Optimization,2008,40: 261-275.

[54] NAGU RNEY A,QING Q,DONG J.Modeling of Supply Chain Risk Under Disruptions with Performance Measurement and Robustness Analysis[C]∥Managing Supply Chain Risk and Vulnerability:Tools and Methods for Supply Chain Decision M akers,Berlin:Springer,2009:91-111.