智能水温控制系统的设计及实现
2011-03-26于光普黎东升尤传富
于光普, 黎东升, 尤传富
(长春工业大学电气与电子工程学院,吉林长春 130012)
0 引 言
目前,水温控制被广泛应用于食品、医药、化工、家电等领域。水温控制系统性能的好坏直接影响产品的品质。因此,研究水温控制技术具有十分重要的意义。
文中所介绍的水温控制系统的控制对象为格来德WKF-9301电热水器(功率1 000 W,容量1.2 L),温度设定范围:水温初值≤99℃,最小区分刻度为1℃;定时加热时间设定范围:2~99 min。温差≤±1℃;时差≤±0.5min。
1 控制器设计
智能水温控制系统的控制器设计主要包括定时加热设计和恒温保持设计两部分。由于水温控制具有一定的滞后特性,且引起这种滞后效应的因素较多,例如加热材料的物理特性、加热过程中水体与外界环境的热能交换以及水体自身受热蒸发所导致的质量变化等,这些因素具有不确定性,因此,水温控制系统的精确数学模型很难建立起来,为了避开这类复杂问题,定时加热控制器以一个近似数学模型为基础,通过采用逐次修正输出校正因子的方法迫使实际输出逐步逼近理论输出。具体控制算法如下。
1.1 定时加热控制设计
由能量守恒定律和水体热量公式可知存在如下数学关系:
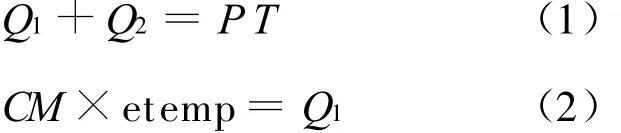
式中:Q1——水体热量;
Q2——损失热量;
P——电热器的电功率;
T——实际加热时间;
C——水的比热容;
M——水体质量;
etem p——温差。
室温条件下,在加热过程中,水体的受热速率大于水体热损速率。因此在一个微小时间区域内,忽略损失热量,则水体热量近似等于电功能量,即:

式中:T1——近似加热时间。
当C=4.2×103J/(kg◦℃),P=1 000W,M=1.2 kg时,有如下近似关系(若实际控制过程中质量损失严重则需引入质量监测):

又由于

式中:setime——设定时间;
setem p——设定温度;
wok time——电热器工作时间;
rtemp——实时水温;
etime——时差。
记etime与T1比率为K,则有如下数学关系:

取1/K作为输出校正因子,若加热方式采用PWM调制交流电压输出周期个数,则PWM的占空比为 100/K。通过不断采样 w oktime和rtem p修正K值,最终迫使T1逐步逼近T。
1.2 恒温保持控制设计
水温控制的另一个特性是具有记忆效应,因此,恒温过程的数字PID控制算法宜采用增量式。与位置式算法相比,增量式算法消去了积分项,因而可消除控制器的积分饱和,在精度不足时,计算误差对控制量的影响较小,易取得较好的控制效果[1]。增量式数字PID公式如下:

为了便于计算机编程,简化计算,提高计算速度,将上式整理为[1]:

式中:K p——比例系数;
K i——积分系数;
Kd——微分系数;
E(k)——当前采样时刻偏差;
E(k-1)——上一次采样时刻偏差;
E(k-2)——上两次采样时刻偏差。
1.3 过渡过程平滑处理
过渡平滑处理过程可分为两种情况讨论:
1)当设定时间与全功率状态下达到设定温度所用的时间相接近时,为了获得较好的时间-温度同步性,选择以下方式:当温度小于某一阈值时停止加热,然后切换到PID控制。一般是将全程温度分成若干档位,每段档位对应合适的阈值和PID参数,按照设定值选择合适的档位即可。
2)当设定时间大于两倍(或者两倍以上)全功率状态下达到设定温度所用的时间时,输出校正因子K随着时间逐渐由大变小,当 K≤2时,PWM的占空比≥50%。这种较大的占空比有利于获得较好的同步性,但是它同样也给后续恒温保持环节带来较大的温度超调。在兼顾同步性的前提下,有效地抑制超调,采取如下平滑处理:
①限幅输出,当温差etemp=2℃且K≤1时,PWM的占空比预取60;
②切换到PID控制,调整参数;
③观察同步性,若不理想,修改占空比,继续调整参数。
2 水温控制系统软硬件概述
2.1 硬件设计概述[2]
智能水温控制系统的控制器选择89C52单片机;温度传感器选择DS18B20;时钟芯片选择DS12C887+;键盘芯片选择MAX 6955;显示器选择青云LCM 128645ZK型液晶。采用串行方式将液晶屏与单片机连接;MAX 6955的P4引脚与单片机的P3.3引脚相连接;单片机的P1.6引脚作为输出口,经过非门后与固态继电器相连接。
2.2 软件设计概述[3-8]
软件整体主要由3部分构成,即一个主程序和两个中断程序。其中主程序负责解决芯片初始化、温度和时间采样显示以及计算分析等问题,其中合理性判别主要分析时间、温度的设置是否合理,即设定时间在1~90倍全功率加热状态下上升到设定温度所需时间之间。定时器 T0每20ms中断一次,通过计数完成周期为2 000 m s的PWM数字脉冲;MAX 6955外部中断函数主要用于按键识别及处理,软件流程如图1所示。
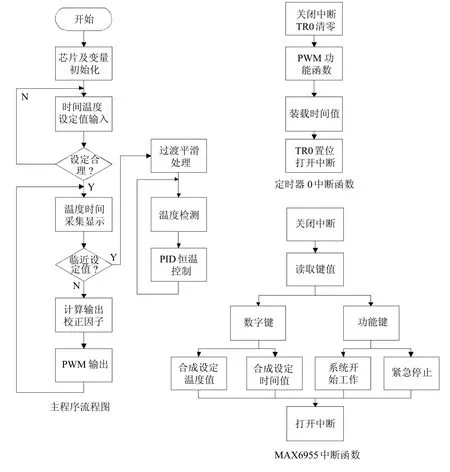
图1 软件流程总图
3 数据及分析
测试时,温度传感器DS18B20在工作过程中选择9位数字输出,转换后的温度值只保留整数位,采样时间小于1 s,在温度发生跳变时记录时间数据。
3.1 实验数据
设定温度为45℃,设定时间为15min,初始水温为12℃,室温为17℃,实验数据见表1。

表1 实验数据
根据上述数据,应用M ATLAB软件绘制实时水温曲线,如图2所示。

图2 水温实时曲线
3.2 结果分析
从初始水温开始,上升1℃所用的时间与后续升温过程中每升高1℃所用时间相比,具有一定的差异。引起这种差异的因素较多,而且比较复杂,但是其影响只在初始水温升高1℃这段时间内表现较为明显,对后续加热过程影响较为微小。因此,这段时间可以作为后续升温的一个参考点。实验数据中存在时间相同而温度值不同的数据对,这主要是由于采样时间较小以及处于温度临界点造成。从初始水温+1℃开始到定时加热结束这段区间,曲线逼近效果较好。通过多次测试发现,当设定时间介于3~10倍的全功率状态下达到设定温度所用时间之间时,可以达到最佳逼近效果。在此范围之外,虽然同步性效果很好,但失真较大。过渡过程中,温度超调为1℃。恒温过程中,稳态误差≤1℃。
4 结 语
通过理论分析和实验验证,基于89C52单片机的采用逐次逼近算法和增量式PID算法设计的智能水温控制系统能够获得较好的控制效果,在实际生产过程中具有一定的应用价值。
[1] 张德江.计算机控制系统[M].北京:机械工业出版社,2007.
[2] 张毅刚,彭喜元,董继成.单片机原理及应用[M].北京:高等教育出版社,2010.
[3] 胡伟,季晓衡.单片机C程序设计及应用实例[M].北京:人民邮电出版社,2003.
[4] 范立南,李雪飞,尹授远.单片微型计算机控制系统设计[M].北京:人民邮电出版社,2004.
[5] 李震,洪添胜.基于AVR单片机和PID算法的水温控制器[J].国外电子测量技术,2006,25(1):47-50.
[6] 张越,张炎,赵延军.基于单片机和模糊控制的水温自动控制系统[J].仪表技术与传感器,2007(4):71-72.
[7] 李铁.基于单片机的温度控制系统的设计[J].微型机与应用,2010,29(24):29-30.
[8] 刘敏.基于A T89S53单片机的电阻炉温度控制系统设计[J].宁夏机械,2008(4):11-13.
