基于修正熵权的TOPSIS 地下水质评价方法

杨玉中，孟祥中，，刘曦，邓叶飞，王晓林

(1．河南理工大学 能源科学与工程学院，河南 焦作454010; 2．河南平原光电有限公司 生产安全部，河南 焦作454001; 3．焦作市机动车排污监控中心，河南 焦作454003)

0 引言

水是生命的源泉，然而中国城市地下水污染日益加剧，据118 个城市监测资料，约64%的城市地下水遭受严重污染，33%的城市受到轻度污染，基本清洁的城市只有3%［1］． 随着城市化、工业化的发展，人们环境保护意识的增强，地下水质量出现不同程度的变化． 科学地对地下水质进行综合评价对于判别水质情况、预报水污染趋势、开展水污染预警管理具有重要的意义．

采用科学合理的评价方法对地下水质状况进行评价是地下水质量评价的核心内容． 根据GB/T 14848—1993［2］地下水质量标准可知，根据地下水分类指标( 监测项目) 综合评价地下水质是一个典型的多属性决策问题，各指标评判结果具有独立性．因此，在地下水质量状况评价中形成了许多综合的评价方法，地下水质量标准采用F 分值评分法，其他评价方法有模糊评判法［3］、层次分析法［4］、人工神经网络算法( BPN)［5］等． 其中F分值评分法无法区分属性的重要程度; 模糊评价法隶属函数的确定较困难，评价主观性较强;层次分析法在属性较多时，判断矩阵容易出现严重的不一致性问题;人工神经网络算法运算过于复杂．

笔者采用修正熵权系数和逼近理想解排序方法( Technique for Order Preference by Similarity to Ideal Solution，TOPSIS) 对地下水质评价的方法进行研究．

1 修正熵权TOPSIS 评价方法

1．1 熵值法确定权重及修正

熵值法是在客观条件下，由评价指标值来确定指标权重的一种方法［6-7］．一般来说，综合评价中某项指标差异程度越大，信息熵越小，该指标提供的信息量越大，该指标的权重越大［8］．

(1) 将m 个可行方案n 个指标值的原始数据xij(i=1，2，…，m; j=1，2，…，n)组成的矩阵定义为X;

(2) 数据标准化:

(3) 计算各指标的熵:

信息偏差度dj为

(4) 计算评价指标的熵权ωj:

(5) 由于决策者对于属性集偏好不同，给出的修正权重的系数为λ，就可以利用λj对熵权进一步修正［9］，得到比较准确计算评价指标的熵权ω0

j:

1．2 TOPSIS 综合评价方法

TOPSIS 综合评价方法计算步骤如下［10-11］:

(1) 建立加权标准化决策矩阵．通过式(5) 得出的权重向量ω0在这一步被考虑到决策矩阵中．加权标准化决策矩阵V 通过矩阵P 的每一列与其相应的权重相乘得到．

(2) 确定理想解和负理想解．令方案A+表示最偏好的方案( 理想解) ，A-表示最不偏好的方案( 负理想解) ，因地下水质评价中所选取的指标都是成本型指标，则有:

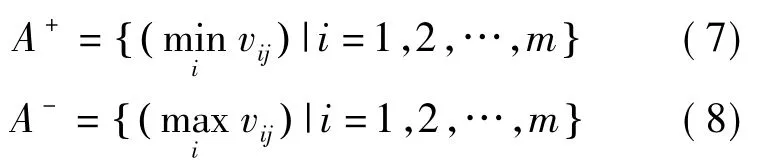
(3) 计算距离．每个方案的距离通过n 维Euclid 距离来测量．每个方案与理想方案的距离为:

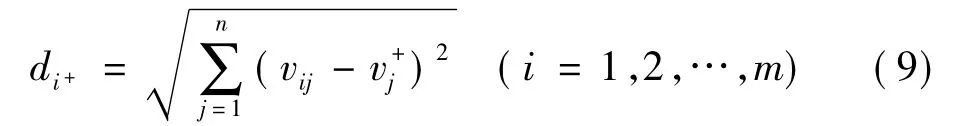
同样，到负理想解的距离为:

(4) 确定相对接近度． 评价对象与理想解的相对接近度为:

(5) 排列偏好顺序． 依据Ci+的降序，方案集此时能按偏好属性排列．

2 C 城市2005—2009 年地下水质的综合评价

C 城市位于河南省西北部，北依太行南临黄河，总面积4 071 km2，总人口345．5 万．按照GB/T14848—1993 地下水质量标准，选取砷、汞、铬( 六价) 、总硬度、铅、溶解性总固体、氯化物共7项评价指标，根据C 城市地下水监测资料，2005—2009 年各项监测结果的平均值如表1． 为便于计算，我们只选取了与该事例有关的GB/T 14848—1993 地下水质量标准中Ⅰ类和Ⅱ类标准．由于不同的监测项目对人们生活的影响有所差别，专家给出了修正熵权的系数为λ =( 0．1，0．2，0．15，0．15，0．2，0．1，0．1) ．

2．1 用熵权法计算权重

(1) 利用表1 中原始数据组成矩阵X:

(2) 利用式(1) 计算pij，得出:

表1 C 城市2005 －2009 年地下水质监测结果与分类标准比较Tab．1 Testing results of groundwater quality from 2005 to 2009 in C city and classification standarol mg/L

(3) 利用式( 2) 、( 3) 、( 5) 分别计算Ej，dj，

E=［0．934 1 0．805 8 0．910 5 0．967 1 0．881 2 0．983 0 0．919 0］;

d=［0．065 9 0．194 2 0．089 5 0．032 9 0．118 8 0．017 0 0．081 0］;

ω0=［0．067 7 0．399 0 0．137 9 0．050 7 0．244 1 0．017 5 0．083 1］．＞2006 年＞2007 年．通过以上计算可以得出Ⅰ类水质与最优值的接近程度为0．827 2，Ⅱ类水质与最优值的接近程度为0．129 3，显然2008—2009年度地下水属于Ⅰ类水质，2005—2007 年度地下水属于Ⅱ类水质．2005—2009 年度地下水质变化趋势可以用图1 清楚地表达出来．

图1 C 城市2005—2009 年地下水质变化趋势图Fig．1 Change tendency figure of groundwater quality from 2005 to 2009 in C city

2．2 TOPSIS 综合评价方法

(1) 建立加权标准化决策矩阵，由式(6) 得:

(2) 确定理想解和负理想解． 因地下水质监测指标都是成本型指标，由式(7) 、(8) 知:

A+={0．001 6 0．012 6 0．009 7 0．004 4 0．007 6 0．001 8 0．004 3}，

A-={0．016 1 0．157 1 0．048 4 0．011 2 0．076 3 0．003 6 0．025 9}．

(3) 计算距离． 由式( 9) 得: d1+=0． 072 5，d2+=0．290 5，d3+=0．055 7，d4+=0．006 2，d5+=0．009 7，d6+=0．031 8，d7+=0．162 9．

由式(10) 得: d1-=0．304 1，d2-=0．884 5，d3-=0．141 6，d4-=0．161 5，d5-=0．163 0，d6-=0．152 2，d7-=0．024 2．

(4) 计算与理想解接近程度． 由式( 11) 得:C1+=0．807 5，C2+=0．752 8，C3+=0．717 7，C4+=0．963 0，C5+=0．943 8，C6+=0．827 2，C7+=0．129 3．

(5) 方案集和评级标准此时的排列顺序为:

C4+≻C5+≻C6+≻C1+≻C2+≻C3+≻C7+

2．3 结果分析

由此可见，C 城市2005—2009 年地下水质量的综合评价排序为:2008 年＞2009 年＞2005 年

3 结论

基于修正熵权的TOPSIS 综合评价方法，既采用信息熵进行客观赋权，又根据监测项目对人们生活影响的强弱，利用专家意见对熵权进行修正，是对TOPSIS 评价方法的进一步研究． 通过对C城市2005—2009 年度地下水质进行综合评价，得出了该城市地下水质属于Ⅰ、Ⅱ类水质，并据此得到该城市地下水质变化趋势． 评价的过程和结果表明该方法计算简单，结论明确，易于推广使用;通过与该城市水质评价资料对比，该结果与实际结果基本一致．

［1］ 尹国勋，李振山．地下水污染与防治:焦作实证研究［M］．北京:中国环境科学出版社，2005．

［2］ 地质矿产部地质管理司，地质矿产部水文地质工程地质研究所，全国环境水文地质站，等． GB/T 14848—1993，地下水质量标准［S］．北京:中国标准出版社，1993．

［3］ 杨铭威，石亚东，盛东，等．城市供水安全评价指标体系初探［J］．水利经济，2009，27(6) : 32 -35．

［4］ 李晋杰，刘生宝，孙国才，等． 基于层次分析法( AHP) 的小城镇地下水饮水安全评价［J］． 中国高新技术企业，2010，21:51 -53．

［5］ 桂祥友，马云东，王文．神经网络在矿区地下水评价中的应用［J］． 辽宁工程技术大学学报，2003，22( S) :148 -150．

［6］ YOSHIAKI Y． Wave front-flatness evaluation by wave front-correlation-information entropy method and its application for adaptive confocal microscope［J］． Optics Communications，2004，232(6) :91 -97．

［7］ MA Jian，FAN Zhi-ping，HUANG Li-hua． A subjective and objective integrated approach to determine attribute weights［J］． European Journal of Operational Reseach，1999，112(2) :397 -404．

［8］ 杨玉中，吴立云，丛建春．基于熵权的煤矿运输安全性模糊综合评价［J］． 哈尔滨工业大学学报，2009，41(4) :257 -259．

［9］ 徐玖平，吴巍． 多属性决策的理论与方法［M］． 北京:清华大学出版社，2006．

［10］杨玉中，张强，吴立云． 基于熵权的TOPSIS 供应商选择方法［J］．北京理工大学学报，2006，26(1) :31-35．

［11］刘茜，吴黎军．新疆某3 所医院的熵权TOPSIS 法综合评价［J］． 数理医药学杂志，2009，22( 3) : 349 -352．