ANSYS Workbench的液压油缸多目标优化设计

彭先勇,陆中良,李受人,王雪萍

(1武汉第二船舶设计研究所,湖北 武汉 430064;2武汉理工大学物流工程学院,湖北 武汉 430063)

随着经济的发展和科学技术的突飞猛进,市场对产品提出越来越严格的要求.依靠经验设计的产品其结构及尺寸参数相对保守,耗材过多,成本过高,性能难以达到最佳.由经验设计向采用CAD/CAE等现代设计方法是产品设计的发展趋势.在保证产品强度、刚度、变形等条件下通过优化设计使产品小型化、轻量化是现代制造产业追求的目标.液压油缸作为车辆,船舶的重要动力装置设备之一,其小型化、轻量化不仅节省了材料,减少了生产成本,而且也降低了运输成本,提高了产品的竟争力.因此液压油缸的优化有着重要的现实意义.本文以某种型号的液压缸为研究对象,运用Ansys Workbench有限分析工具及其优化模块,对缸壁厚度、活塞行程与应力、应变、质量等关系进行探讨,提出了其小型化、轻量化的最优解.

1 液压油缸系统建模、网格划分

液压油缸系统的零件比较多,由于细部的零件挡环,阀座等部件对于整体的影响不大,所以建模时将其忽略.简化后模型主要由缸筒部分和活塞部分组成.由于整个系统的对称结构,建模时只须建出其对称的一半模型即可.系统在活塞杆完全伸出时工况最为恶劣,所以以活塞杆此时的液压油缸为研究对象.在Pro/E中建模(当前缸筒壁厚 25.5 mm,缸筒的内径115 mm,行程1096 mm),简化后的模型如图1所示.通过ANSYS Workbench与Pro/E的接口将其导入.采用物理结构自动网格划分功能,控制单元尺寸为0.01 m,划分的网格如图1所示,共含有节点130867个,单元73224个.

整个系统有三处接触:活塞与缸筒内壁的接触,将其定义为无摩擦接触;活塞与缸筒底壁部分的接触,将其定义为不分离接触;活塞杆与缸筒部分的接触,将其定义为无摩擦接触.

对于液压油缸系统的负载主要有三个,一端铰的固定负载,无杆腔的压力载荷,一端铰接的外负载.无杆腔工作压力为31.5 GPa,折算到外负载的为1200 kN.由于选取了工作台结构的1/2进行分析,故还要施加对称约束.加载,得到系统的应力、径向应变云图(图2).由图可以看出,缸筒部分应力相对集中,主要处于100～200 MPa,而且内壁部分的应力高于外壁部分应力,但是相对于45钢的屈服极限360 MPa,还有很大的优化空间.径向应变也主要集中在缸筒部分.因此缸筒部分是研究的重点.

2 理论计算及影响液压油缸重量因素分析

影响液压缸重量的因素主要有缸筒的壁厚、缸的长度(活塞行程)和缸筒所用的材料.同时液压油缸为高压容器,其缸筒厚度、活塞的行程和材料决定了其能够承受压力.因此在压力一定的情况下,缸筒的轻量化、小型化即对壁厚和行程的优化或者是选用其他的材料.按钢制压力容器标准得如下应力、应变计算[1].缸筒应力

其中:Di为缸筒的内直径;pc为内压力;δe为缸筒的厚度.缸筒的轴向应变

式中:L为缸筒原长度;Δ l为轴向变形量;E为拉压弹性模量.缸筒径向应变

由式(1)～(3)可以看出缸筒的应力、应变与缸筒的厚度、内直径直接相关.分别代入Di=230 mm,pc=31.5 MPa,δe=25.5 mm,E=2.1 GPa,计算出理论的 σt=158 MPa,ε=0.207 mm,ε'=0.1 mm.与有限元计算结果的较为相近,说明了有限元计算可信.因此,以下通过有限元计算方式来进行相关的问题研究.

以上计算结果和Ansys-Workbench应变云图可知缸筒部分的应变较小,最大的径向应变仅0.1 mm,可不考虑应变部分的影响.以缸筒质量为优化目标,分别考虑其在材料允许的应力范围内的最小化.用Ansys Workbench的目标驱动优化分析模块进行仿真计算[2].

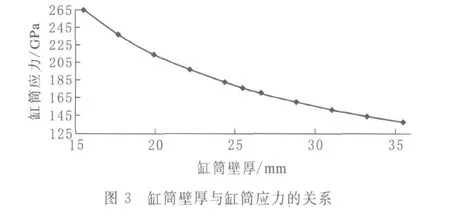
2.1 缸筒壁厚与缸筒应力、质量的关系

控制缸筒的内径和行程不变,定义缸筒的壁厚为变量,由仿真计算得出其与缸筒的应力、质量的关系如图3、图4所示.

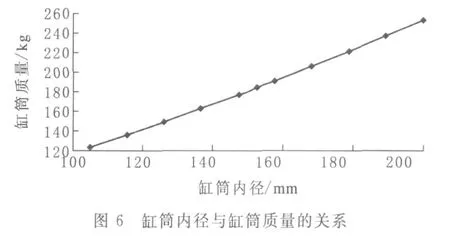
2.2 缸筒内径与缸筒应力、质量的关系

控制缸筒的壁厚和行程不变,定义缸筒的内径为变量,由仿真计算得出其与缸筒的应力、质量的关系如图5、图6所示.

2.3 活塞行程与缸筒应力、质量的关系

控制缸筒的壁厚和缸筒内径不变,定义活塞的行程为变量,由仿真计算得出其与缸筒的应力、质量的关系如图7、图8所示.

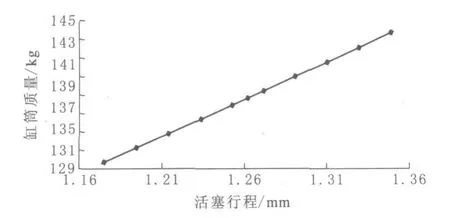
图8 活塞行程与缸筒质量的关系

3 优化设计

由以上仿真分析的结果可以得缸筒的应力随着缸筒的壁厚的增加而减少,随着缸筒的内径的增加而增加.缸筒的应力与活塞行程无关.因此液压缸系统的轻量化主要从壁厚和内径着手.以当前缸筒壁厚25.5 mm为例阐述其优化过程.

取缸筒的材料为45钢,其弹性模量取E=210 GPa,泊松比μ=0.3,密度ρ=7800 kg/m3,屈服极限为360 MPa,取安全系数为1.5,则材料对应的可以承受最大应力为360/1.5=240 MPa.由图3看出当前壁厚25.5 mm时,对应的缸筒部分应力为173 MPa,因此该缸存在优化的空间.由图4可以看出当取壁厚17.5 mm左右时,缸筒部分的应力大约为239 MPa,此时材料应力性能发挥到最大.设定该部分的优化的目标如下:最大应力≤240 MPa,其优先级为最高;质量在应力满足条件下取最小值,其优先级次之;变形量优先级最低[3].由计算机计算得到的推荐优化解如表1所示.由表1可以看出壁厚取值17.4 mm时比较合适.将该值再回代入原模型计算得出相应的值如下表2所示.

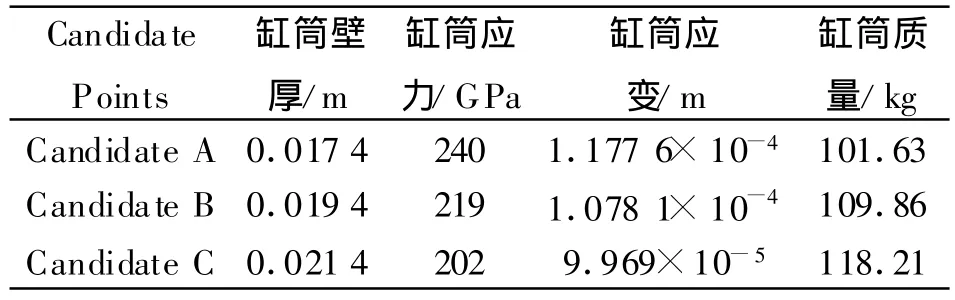
表1 优化解

表2 回代入原模型校核值

表3 优化前后各项数据对比

由表3可以看出,优化以后缸筒部分的应力较优化以前增加,但仍在安全系数的范围内,应变也仅为0.11 mm,但是缸筒的质量由135.7 kg降到了101.kg,降低了25%.可见优化计算后的缸筒材料得到更好的发挥,重量得以减轻.

以缸筒内径做优化与以缸筒壁厚优化类似,不再赘述.换作其他材料时,将相关材料的性能参数更改即可,不再赘述.

4 结束语

本文应用ANSYS Workbench的有限元计算及多目标优化设计功能,对影响液压缸系统的内部应力因素进行了分析.以缸筒壁厚部分的优化为例,阐述了在满足系统应力,应变要求的前提下,减轻缸筒质量.与传统的方法相比,该设计方法提高了材料的利用率,降低了企业的生产成本,为此类系统的相似部件结构优化和其他系统的结构优化设计提供了一种高效、可行的方法.

[1]全国压力容器标准技术委员会.GB 150-1998钢制压力容器[S].北京:石油工业出版社,1998.

[2]李 兵.ANSYS Workbench设计、仿真与优化[M].北京;清华大学出版社 2008.

[3]浦广益.ANSYS Workbench12基础教程与实测详解[M].北京:中国水利水电出版社,2010.