离散型卡尔曼滤波在汽车零部件检测中的应用

郑家旺,刘有源

(武汉理工大学物流工程学院,湖北 武汉 430063)

卡尔曼滤波是从与被测信号有关的观测中通过算法估计出所需信号的一种最优化自回归数据处理算法.由于卡尔曼滤波具有最小无偏方差性,目前广泛应用于机器人导航、控制、传感器数据融合、设备状态检测和计算机图像处理等领域.卡尔曼滤波与其他传统的滤波器相比,最大的特点是能够去除测量系统中的随机误差,来获取更接近真实值的信息.

1 离散型卡尔曼滤波的数学模型

卡尔曼滤波有连续和离散型两种算法,其中离散型算法目前被广泛应用于线性系统的状态估计中.

设tk时刻的状态估计为X(k),系统噪声序列为W(k),则状态方程[1-3]可描述为

对于X(k)的测量满足线性关系,测量方程为

其中,F为转移矩阵,Γ为系统噪声矩阵,H为测量矩阵,v(k)为测量噪声序列,W(k)为状态方程的过程噪声序列.则卡尔曼滤波的方程为:滤波估计

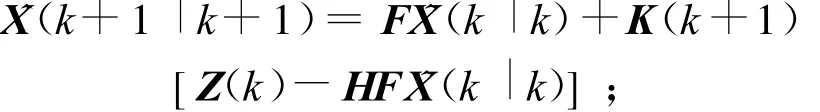
滤波增益

单步预测误差协方差矩阵

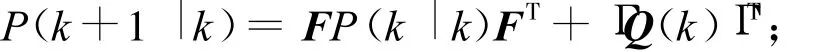
滤波误差协方差矩阵

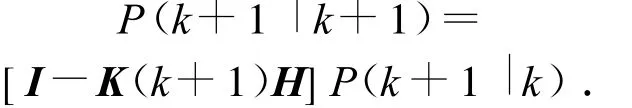
需要指出的是,P(k+1|k+1)可以看作Kalman滤波的性能评价,因为

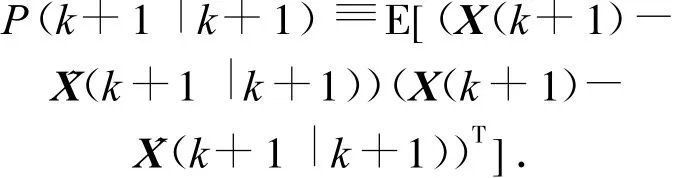
卡尔曼滤波流程如图1所示.可见,只要给定初值P0,根据tk时刻的测量值Z(k),就可以递推计算得到k时刻的状态估计 X(k).

图1 卡尔曼滤波基本流程

2 卡尔曼滤波仿真

在卡尔曼滤波中,有时候会出现一种现象:随着测量值的不断累积,按照滤波方程计算的估计误差方差矩阵会逐渐趋于一个稳定值,但估计值相对实际测量值被估计误差却逐渐增大,使示波器逐渐失去作用,这种现象被称为卡尔曼滤波器的发散.

引起滤波器误发散原因主要有:1)描述该系统动力学特性的数学模型和噪声的统计特性与真实的物理过程有偏差;2)在卡尔曼滤波的递推过程中,随着滤波次数的增加,舍入误差逐渐积累.

2.1 该滤波算法收敛性的验证

通过MAT LAB来验证该滤波器的收敛性[1].初值的确定如下.

测量时间Measure=100 s.由于频率太高会导致数据量增大,导致MATLAB中仿真时运行较慢,所以周期T=0.01 s;q=0.01;r=0.01;

仿真结果如图2所示.

图2 卡尔曼滤波MATLAB仿真

通过图2可见,在该参数下设计的卡尔曼滤波器是收敛的,且收敛速度较快.在提高数据的精度方面,滤波之后的误差远小于原始误差.

2.2 滤波效果验证

在设计中采用VC++6.0编程[5],对该滤波算法的效果进行检测.初值的确定如下.

由于VC++6.0能够调用系统底层资源,运行较快,所以周期 T=0.001 s;q=0.01;r=0.01;

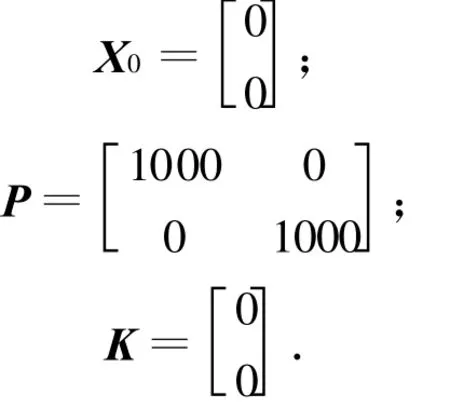
设采样函数为y=2t;高斯噪声函的均值为0,方差为0.5.

施加噪声函数之后的采样函数如图3所示,卡尔曼滤波之后的采样函数如图4所示.

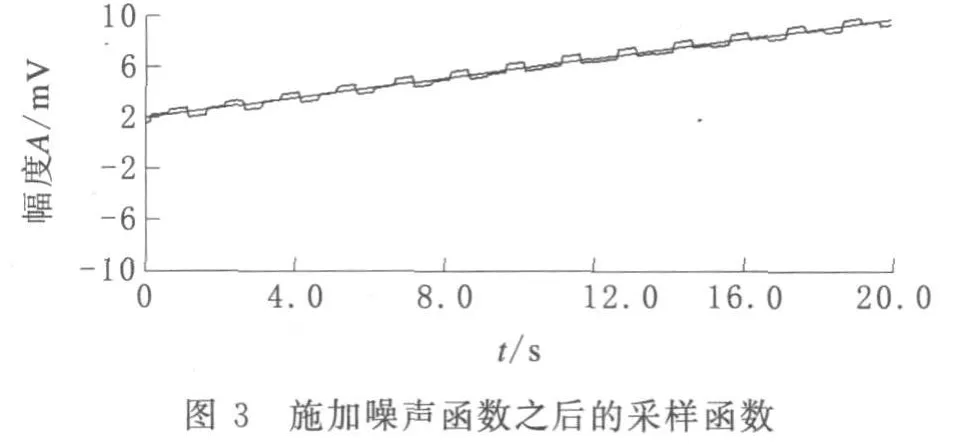
图3中,采样函数在添加了白噪声之后,系统出现明显的波动.图4中,在卡尔曼滤波之后,系统经过短暂的波动,逐渐与采样函数接近,滤波效果较好.对比图3和图4可见,该滤波器对于白噪声的滤除效果较好,能够对采集的数据进行较准确的修正.

3 结束语

在卡尔曼滤波算法的设计过程中,一般需要根据提前观测的信息,确定系统的数学模型,以较好地拟合动态系统的变化规律,提高修正数据的精度.对于一个稳定的系统,只要能够确保初始值的精度,就可以达到指定的精度.

[1]谢克明.现代控制理论[M].北京:清华大学出版社,2007.

[2]蒋志凯.数字滤波与卡尔曼滤波[M].北京:中国科学技术出版社,1993.

[3]邓自立.卡尔曼滤波与维纳滤波[M].哈尔滨:哈尔滨工业大学出版社,2001.

[4]余祖锋,许才军.Matlab在测量中的应用[J].东北测绘,2004,25(4):43-46.

[5]孙 鑫,余 安.VC++深入详解[M].北京:电子工业出版社,2006.