通道不平衡对偏置相位中心多波束SAR性能影响的理论分析
2011-03-22郜参观邓云凯
郜参观 邓云凯 冯 锦
①(中国科学院电子学研究所 北京 100190)
②(中国科学院研究生院 北京 100039)
1 引言
由于具有全天时、全天候的成像能力,合成孔径雷达(SAR)已成为对地观测不可或缺的手段之一[1]。随着技术上的进步和用户对图像质量需求的提高,目前的合成孔径雷达普遍要求具有高分辨率-宽测绘带成像能力。高分辨率SAR图像能提供目标的细节信息,宽测绘带 SAR在给出大尺度图像的同时,可以降低观测动态目标时的重访时间。
按照奈奎斯特采样定理,为了避免方位向模糊,雷达脉冲重复频率(PRF)必须大于多普勒带宽。但PRF的提高同时又受距离向测绘带宽的限制,这即是对于传统模式SAR来说的最小天线面积约束。当设置多接收孔径时,合成孔径雷达能够突破单孔径接收时的最小天线面积约束。目前,多接收波束SAR可分为距离向多波束SAR和方位向多波束SAR两种,方位向多波束SAR又细分为单相位中心多波束SAR(single phase center multiple-beam SAR)和偏置相位中心多波束 SAR(displaced phase centers multiple-beam SAR)[2]。其中,偏置相位中心多波束SAR由于更易于工程实现而得到更多的关注。但偏置相位中心多波束SAR对PRF的选择有严格的限制,在星载条件下这会产生非均匀采样问题[3,4],同时多个接收通道间的不一致性问题也会降低 SAR图像质量[5−9]。
本文重点关注接收通道间的不一致性对偏置相位中心多波束SAR性能的影响问题。目前,相关文献中已提出了一些通道不平衡的补偿方法,主要有基于原始数据的方法和内定标方法。基于原始数据的方法主要有空时自适应滤波法、子空间投影法等[5−7]。文献[8,9]则利用内定标方法实现了通道间的不一致性补偿。但是这些文献并未对通道不平衡对SAR性能的影响作系统性的理论分析,包括假目标位置和假目标电平相对大小的影响性因素等,而这对于偏置相位中心多波束 SAR的系统设计来说又是必不可少的。
本文接下来的内容安排如下:第2节对偏置相位中心多波束SAR的原理作基本阐述;第3节从理论上推导通道间的不一致性对方位向脉冲压缩的影响;第4节为仿真部分;最后是结束语。
2 偏置相位中心多波束SAR基本原理
如图1所示,以3通道为例来阐述偏置相位中心多波束SAR的基本原理。不妨设中间的子孔径发射线性调频脉冲信号,接收时,3个子孔径同时接收从目标反射的回波。实子孔径相位中心用矩形来表示,实子孔径间的距离为d;等效子孔径的相位中心用圆形来表示,它位于发射子孔径和接收子孔径连线的中心。Rt(η)表示发射孔径与目标之间的距离,Rm(η)表示接收孔径与目标之间的距离。第m个子孔径的接收基带信号可表示为[1,4]

图1 偏置相位中心多波束SAR工作原理示意图
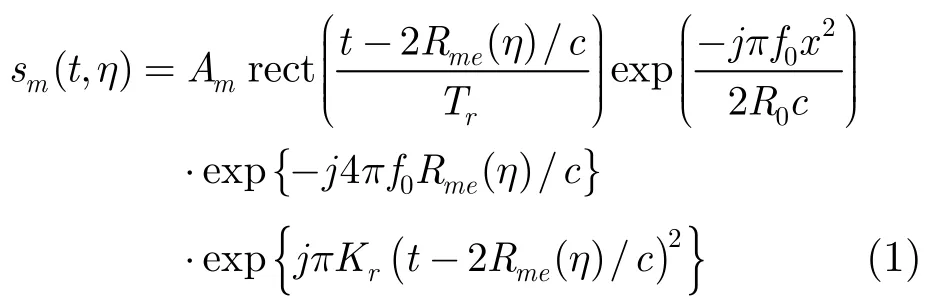
其中Am表示与m子孔径通道特性相关的常数,t为快时间,η为慢时间,Kr为调频率,f0为工作中心频率,c为光速,Tr为发射脉冲宽度,rect(·)为矩形脉冲函数,R0为雷达与目标间的最短斜距,x为接收子孔径相对发射子孔径的距离,Rme(η)表示等效子孔径与目标之间的距离。式(1)中的第1个指数项为相位补偿项,当x≪R0时,该项可忽略。当M个子孔径的偏置相位中心多波束 SAR的通道特性一致且脉冲重复频率满足

时,它就与以M·P RFDPC为脉冲重复频率的单孔径SAR等效,从而达到降低脉冲重复频率提高距离向测绘带宽的目的。式(2)中,vp为雷达的移动速度。当脉冲重复频率不满足式(2)时,即会产生非均匀采样问题。
3 通道不平衡对方位向脉冲压缩的影响
从上一节的分析可知,当各通道特性一致时,偏置相位中心多波束SAR可以与单孔径SAR等效。然而在工程实现时,由于各通道的前端组成部分,如天线、微波器件、A/D变换器等的工作性能不可能完全一致,且这种不一致性会随着外界环境的变化而改变,这样就有必要分析这种非理想性对多波束SAR性能的影响。在接下来的分析中,假定方位向信号为严格的线性调频信号。同时,不考虑距离向的影响,这样问题就可以简化为1维的。
设一个复数形式的线性调频信号为

其中η表示慢时间,Ka表示调频率,Ta为脉冲宽度。由驻定相位原理可得Ba=KaTa为线性调频信号的带宽。当对s(η)作单通道采样时,为了避免频谱混叠,最低复采样频率必须大于信号带宽Ba。设单通道采样频率为fs=αsBa,其中 αs> 1为过采样率。
为了降低采样频率,可采用多个通道联合采样的方式。假设有M个通道,则对于单个通道来说,其采样频率可降低为fs/M,如图2所示。设第m个通道采样得到的序列为sm(nMTs),其中m=0,1,…,M−1,Ts表示单通道采样时所需的采样周期(在接下来的相关表达式中将被省略),n表示与采样时刻相关的整数。若将这M个序列重新排列即可得等效采样序列s(n)。

图2 线性调频信号的多通道采样
为了分析的需要,现将每个单通道采样序列(nM)的采样点间补上M−1个零,得新的序列(n)。不难发现,这M个新序列叠加可得等效采样序列s(n),即

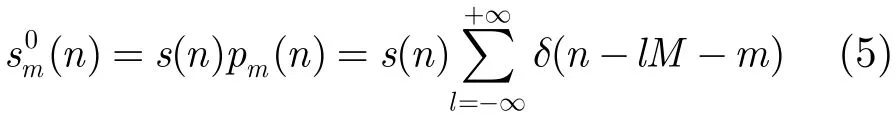

在对信号作数字处理时,求信号的频谱是通过离散傅里叶变换来完成的,而此时所能观察到的频率范围是。为了表达方便起见,将数字频率用模拟频率来表示,所以单通道采样补零序列(n)的频谱可表示为
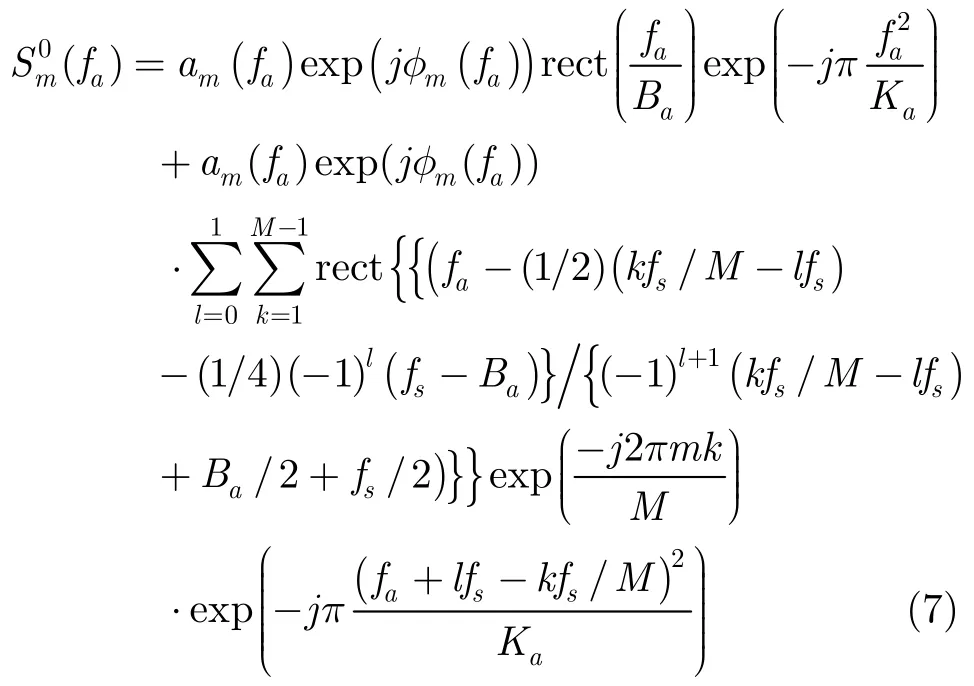
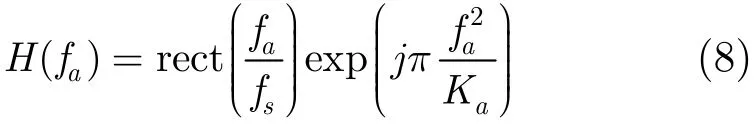

图3 单通道采样补零序列 (nTs)的频谱推导示意图
根据式(4),式(7)可得脉冲压缩结果为

其中“⊗”表示卷乘,S(fa)为s(n)的傅里叶变换,am(η)为的傅里叶逆变换。当各孔径的天线方向图一致,且合成孔径时间较短时,可以假定与频率无关,则式(9)退化为

其中fl,k(η)是为简化书写而引入的函数。am,φm分别表示与通道特性有关的幅度常量和相位常量。当通道特性一致,即时,式(9)成为

由式(11)可知,通道特性一致的情况下无假目标存在。当通道特性不一致时,由式(9)可知,这种情况下有2(M−1)个假目标存在,假目标的位置为

其中l=0,1,k=1,2,… ,M−1。值得注意的是,当运用式(12)计算所得的结果超出的范围时,应对其按Ta取模以使其拉回到的范围内。定义 POSl,k处假目标的峰值-假目标比为假目标电平大小与真实目标电平大小的比值。当通道特性与频率无关时, POSl,k处对数形式的峰值-假目标比为

从式(12),式(13)可以看出,假目标在真实目标两侧按照其位置和电平大小是成对出现的,即
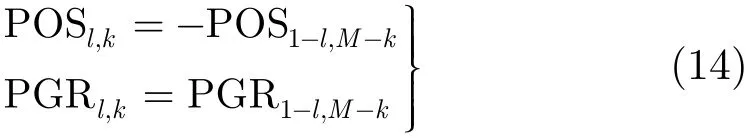
4 仿真分析
由上一节的分析可见,当各通道特性不平衡时,在真实目标的两侧会出现若干虚假目标,假目标的位置由式(12)决定,峰值-假目标比的计算公式由式(13)给出。通道的特性由两个因素决定:器件和天线方向图。其中,天线属于开放系统,所以在工作时其特性很难准确测量,由它引起的不平衡在补偿时也相对比较困难。由于本文不关心具体的通道补偿问题,同时为了使分析简化以明了影响多波束SAR性能的主要参数,所以在下面的仿真中,假定通道间误差为常量。
按照表1中给定的参数进行仿真。表1中的多普勒带宽为177 Hz,方位向过采样率为1.2,所以对于单孔径 SAR来说其采样频率为177 Hz×1.2=212.4 Hz。对于3孔径的多波束SAR来说,每个孔径的采样频率降为212.4 Hz/3=70.8 Hz。

表1 点目标仿真参数
参考图1,设右、中、左 3个子孔径分别称为子孔径0、子孔径1、子孔径2,其通道特性分别为a0exp(jφ0),a1exp(jφ1),a2exp(jφ2)。仿真中,分别考察幅度不平衡和相位不平衡对成像性能的影响。设各个通道的幅度满足m=0,1,2,其中 Inbaam为度量各通道幅度差异性大小的变量,这里称为幅度不平衡度。类似地,设各个通道的相位满足 φm=φ0+m·In bapha,m=0,1,2,其中 Inbapha为度量各通道相位差异性大小的变量,称为相位不平衡度。如图4,图5所示为点目标的仿真成像结果,其中的幅度不平衡度为 0,相位不平衡度为20°。可见,由于通道不平衡的存在,方位向上出现了不希望的4个虚假目标。现对幅度不平衡度和相位不平衡度进行扫描,考察方位向积分旁瓣比和峰值-假目标比的变化情况,结果如图6,图7所示。其中,积分旁瓣比以文献[1]中给出的定义为准,主瓣宽度取3 dB宽度的2倍。图6,图7中,PGR-1表示 POS0,1和 POS1,2处的峰值-假目标比,PGR-2表示 POS0,2和 POS1,1处的峰值-假目标比。仿真时,假目标电平取 PGRl,k和 PGR1−l,M−k中较大者。由图6,图7可以看出假目标电平和积分旁瓣比均随着通道不一致性的增加而增加,且仿真值和本文给出的理论计算值间有较好的吻合。

图4 通道不平衡时点目标成像结果

图5 通道不平衡时点目标成像结果的切片
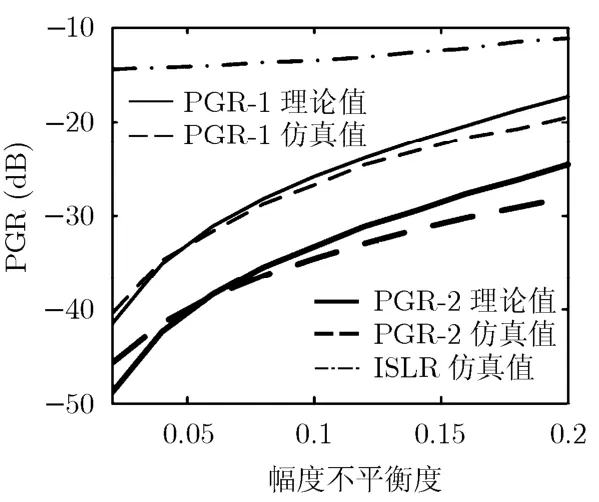
图6 幅度不平衡对假目标电平和积分旁瓣比的影响

图7 相位不平衡对假目标电平和积分旁瓣比的影响
5 结束语
本文分析了通道不一致性对偏置相位中心方位向多波束SAR性能的影响。理论分析表明由于通道不一致性的影响,方位向脉冲压缩时会出现不希望的假目标,假目标的数量、位置及信号大小与通道数、方位向的过采样率及通道不平衡程度等因素相关,文中给出了假目标位置和假目标电平相对大小的计算公式,点目标2维仿真结果验证了公式的正确性。本文假定了通道间的失配为恒定值,但实际运用中由于天线方向图不一致等因素的影响 ,通道间的幅相失配会存在一定的起伏,关于这个问题值得作进一步研究。
[1] Cumming I and Wong F. 洪文, 胡东辉, 等译. 合成孔径雷达成像—算法与实现[M]. 北京: 电子工业出版社, 2007: 2-3, 96.
[2] Currie A and Brown M A. Wide-swath SAR [J].IEE Proceedings–F:Radar and Signal Processing, 1992, 139(2):122-135.
[3] Gebert N and Krieger G. Azimuth phase center adaptation on transmit for high-resolution wide-swath SAR image [J].IEEE Geoscience and Remote Sensing Letters, 2009, 6(4):782-786.
[4] Gebert N, Krieger G, and Moreira A. Digital beamforming on receive: techniques and optimization strategies for highresolution wide-swath SAR imaging [J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 564-592.
[5] 张磊, 金英汇, 刑孟道, 等. 一种子空间投影的高分辨宽测绘带SAR成像通道均衡方法[J]. 电子与信息学报, 2010, 32(1):1-6.Zhang Lei, Jin Ying-hui, Xing Meng-dao,et al.. An SSP based channel calibration for high-resolution and wide-swath SAR imagery [J].Journal of Electronics&InformationTechnology, 2010, 32(1): 1-6.
[6] Jing Wei, Xing Meng-dao, Qiu Cheng-wei,et al..Unambiguous reconstruction and high- resolution imaging for multiple-channel SAR and airborne experiment results [J].IEEE Geoscience and Remote Sensing Letters, 2009, 6(1):102-106.
[7] Li Zhen-fang, Bao Zheng, Wang Hong-yang,et al..Performance improvement for constellation SAR using signal processing techniques [J].IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 436-452.
[8] Zhang Xu-jin, Zhang Chang-yao, and Deng Hai-tao.Channels equalizing and calibration technology of moving target detection for multi-phase centers receive system [C].1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 154-158.
[9] Chen Ren-yuan, Jiang Kai, Yong Yan-mei,et al.. High resolution dual channel receiving SAR compensation technique [C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 713-717.
[10] 胡广书. 数字信号处理—理论算法与实现(第 2版)[M]. 北京:清华大学出版社, 2003: 410-412.
