不确定需求情景下的一种城市物流中心选址方法＊

王淑珍，和振兴

(1.四川工商职业技术学院管理工程系，四川成都610831; 2.中铁二院工程集团有限责任公司地铁设计研究院，四川成都610031)

物流中心选址涉及到很多因素，是一项复杂的工程。国内外学者做了大量的研究工作［1－4］。任永昌等［1］采用重心模型及经济分析法对城市物流中心单点选址模型优化及方案评选进行了研究。周爱莲等［2］运用随机机会约束规划方法，将不确定条件下选址分派费用的波动均方差融入目标函数以实现选址稳健性目标。Killmer［3］在需求、供应、运输费用都不确定的条件下，针对危险品设施选址问题构建了鲁棒优化模型。这些模型虽然比传统选址数学模型具有明显优势，但考虑到预测的需求情景或者与预测需求情景靠近的情景在整个物流中心运营期间持续发生的概率很小，准确性仍受到各种不确定因素的影响。

本文基于情景分析法的基本思想，在不确定需求情景下，通过构建鲁棒优化模型对城市物流中心选址问题进行研究，即物流需求在受到环境小的扰动变化后，物流中心选址的最优解不变。一方面由此模型得出的最优解要接近任意特定情景下的最优解(具有解的鲁棒性);另一方面对不确定参数来讲，最优解逼近零误差(模型具有鲁棒性)，并通过实例及数据分析比较以验证其合理性和实用性。

1 模型的构建

设G=(V，E)表示某一城市物流网络，其中，V=(1，2…，n)表示物流中心的备选点及货物需求点;E=(eij|i，j∈V，i≠j)为两顶点之间的连接边，即物流线路集合，假定网络图已明确而详细地列出了所有的候选路径。设ξ为定义在概率空间(Ω，Α，Pr)上的随机向量，即ξ=(ξ1，ξ2，...ξm)，对每个需求情景ω∈Ω，ξj(ω)为在情景ω下客户j的随机需求量，pω表示需求情景ω出现的概率。定义变量为在需求情景ω下从物流中心i向需求区域j的运量为在情景ω下的物流中心i的货流损失量;capi为物流中心备选点i的最大容量;pc为容量短缺引起单位货流损失的惩罚因子;为需求在情景ω下的中心i容量剩余量;pd为剩余单位容量的惩罚因子。

则具有鲁棒性的城市物流中心选址模型的目标函数描述为:

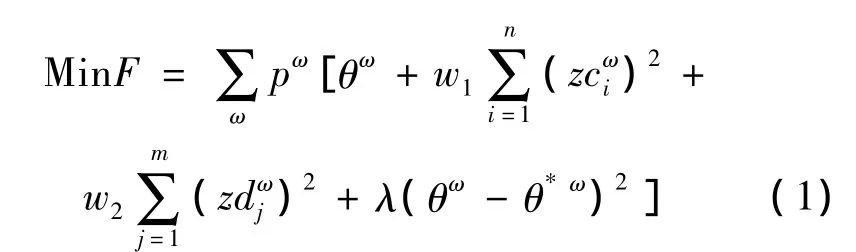
其中:

这是一个非线性规划模型，目标是最小化式(1)和(2)的期望值费用及其偏离最优解的偏移量。模型的鲁棒度量因子wi迫使模型产生在所有情景下使容量短缺与剩余都趋于零的解;解的鲁棒度量因子λ迫使模型找到使各个情景费用都逼近最优解的解。通过变化惩罚因子λ和wi，观测其引起的费用期望值和误差的变化情况来获得。

由此可得基于鲁棒性的物流中心选址方法的完整模型如下:

约束方程(5)保证了必须考虑所有的需求量，要么在此系统中得到满足，要么由别家企业提供(货流损失);(6)保证了中心i的容量利用，要么用来处理货流量，要么空余浪费(容量过剩);约束方程(7)对各备选点能够建设物流中心的最大容量进行了限制;约束方程(8)为运量、容量的非负约束。

2 求解算法设计

鲁棒优化模型是在考虑物流中心的运营过程中其环境参数(需求量)变化的基础上建立的，并通过在具体的区间内改变λ和ω对模型求解。由于其目标函数式(1)是一个非线性方程，因此称其为非线性规划模型，当模型规模很大时，可以采用lingo软件或者GAMS软件求解。思路为:

首先，在运行鲁棒性模型之前，必须先求解得各情景在确定发生情况下的最优解，以作为鲁棒性模型的解的参照物。

其次，求解鲁棒优化模型，通过系统改变w和λ，反复运行线性规划模型求解程序的过程，循环次数为w×λ，算法流程如图1。

3 实例应用及数据分析

以某城市为例，鉴于城市的发展战略，在考虑各个区的社会经济、区域面积、人口密度及其分布、产业分布情况、地理特征等因素，从区域经济学的角度出发［5－6］，将城市按配送范围及配送量分成15个小区，即为各需求点，记为 vi(i=1，2……15)。其网络图如图2所示。

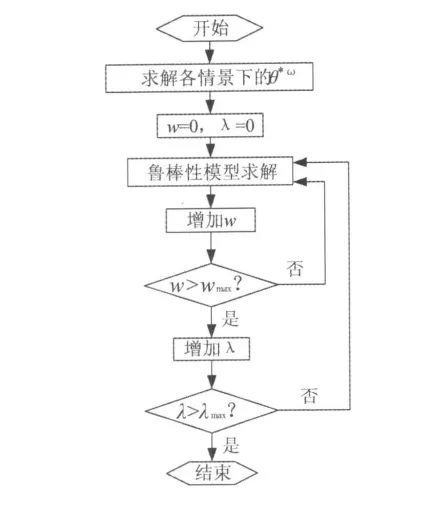
图1 鲁棒性模型的算法流程Fig.1 Algorithm for robustmodel

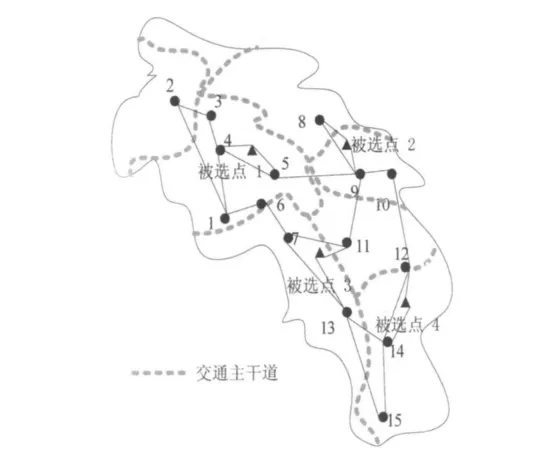
图2 某城市需求点与备选中心点分布示意图Fig.2 Distribution diagram of demand and origin facility center

根据城市发展过程中各区域的战略定位，物流需求现状和发展趋势，将城市物流划分为3个区:Ⅰ区的地理位置优越，物流需求已经具有了一定的规模，规划年内物流需求仍会增长，但增长能力逐年有下降的趋势，包括需求点3，7，11，12，13;Ⅱ区有需求点1，2，5，10，14，有较强的发展潜力，物流中心的建设对于拉动2区发展意义重大，物流较前期物流需求增长速率有较大幅度上升;Ⅲ区包含需求点4，6，8，9，15，有明显的地域特色和特殊环境，物流发展将比较缓慢，需求增长速率到规划年会有所上升，但幅度较小。

通过对未来城市经济发展水平、人口增长速度、产业结构、市场环境及政策刺激等物流不确定影响因素及影响机制的分析及量化，进行典型情景设置，预测规划年内可能的物流需求情景，并分别确定各情景下各区物流需求的增幅大小及各情景出现的概率［7－8］。本例设规划年内有4个需求情景，记为e1，e2，e3，e4，发生的概率分别为0.2，0.3，0.25，0.25。各情景下各需求点的需求量大小如表1。

假定有4个物流中心备选点如图2，各自的最大可能容量为500，建设和经营单个物流中心的单位成本费用(DC)为1.1元/t。各中心备选点到各需求点的单位费用如表2。

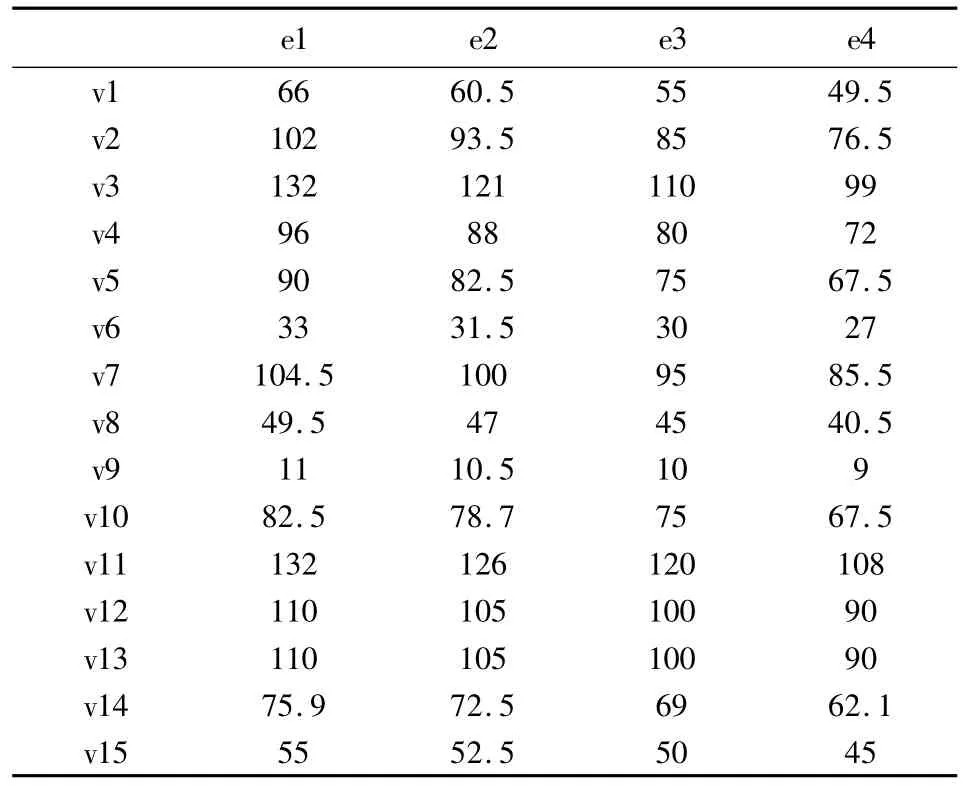
表1 各需求点在各情景下的需求量Table 1 Demands of all scenarios t

表2 各中心备选点到各需求点的单位费用(元/t)Table 2 Unit costs between origin facility centers and demands (yuan/t)

取pc=18，pd=6，运用图1的计算流程，得具有鲁棒性物流中心的最佳适建点为备选点1，2，4，其容量大小分别为:340，384，406 t。

3.1 解的鲁棒性分析

解的鲁棒性由参数λ来控制，本模型中λ的取值范围是［0.00001，0.01］，以步长0.00001进行增加。λ的增大意味着模型强制性找到一个逼近最优解的方案的程度增大。图3描述了在鲁棒性方案下随着鲁棒因子变化时其期望值费用与各自确定发生条件的优化费用的偏移大小示意图。当λ增大到0.0018以前，解基本上是稳定的，没有大的变动。事实上，当λ低于0.002时，鲁棒性模型的解逼近最优解。解得鲁棒性通过协调容量剩余或短缺水平来获得。

图3 鲁棒因子对费用偏移期望值的影响Fig.3 Average cost deviations in robust solutions asλis varied

3.2 对容量短缺或剩余的控制

为了获得逼近容量的零剩余及零短缺对w1，w2在区间［0.00001，0.01］上以步长0.00001实行很微小的变化。然而，要获得在所有情景下都实现零剩余和零短缺的容量方案是不可行的，但是容量的剩余或短缺程度可以通过改变备选点1，2，4这3个物流中心的规划容量来调整。

3.3 鲁棒优化方案与随机规划方案的比较

令w=0，λ=0，则得优化期望值总费用的随机规划模型，与鲁棒优化方案进行对比分析得各情景在2种方案下的费用曲线示意图如图4。由图中可得，除了在随机规划方案下容量短缺非常严重的一些情景外，基于鲁棒性优化的方案(λ= 0.002)大多数情景下比随机模型方案的运营费用要高一点，但是差距不大。

图4 各情景下的费用曲线Fig.4 Cost curve of all scenarios between stochastic solution and robust solution

另外，随机优化方案只是最小化期望值费用，当有些情景出现的时候，可能会由于物流中心容量严重不足，导致费用急剧上升。而鲁棒优化方案的最大优势在于可以大大降低最坏情景的最大后悔值，减小投资的风险。

两方案下各情景货流损失或容量剩余情况对比如图5所示。

图5 货流损失及容量剩余对比Fig.5 Comparison of excess capacity and unmet demand

由图5可得，若实施随机优化方案，则各情景发生的机会损失期望值费用为1 107.63元;发生情景1时，为最不利情况，造成的最大后悔值为: 149.5×18=2 691(元);若实施鲁棒优化方案，则各情景发生的机会损失期望值为918.9元，发生情景1时，也为最不利情况，但这时的最大后悔值为: 118.0×18=2 124(元);因此，无论从最小化期望值费用来讲，还是从最小化最坏情景下的最大后悔值来讲，鲁棒优化方案都优于随机优化方案。

4 结论

(1)在不确定需求情景下，构建及实现了基于鲁棒性优化的城市物流中心选址模型。实例分析表明，此模型不仅可以最小化期望值总费用而且可以大大降低最坏情景的最大后悔值，减小投资风险。

(2)该模型可以进一步推广到供应、运输费用等其他因素的不确定性处理，以进一步提高选址在整个运营过程中的稳健性。

(3)解决了将不确定因素假设为若干情景的选址问题，对于费用因素的不确定性以某一函数形态出现时，选址模型还需进一步研究。

［1］任永昌，刑 涛，赵国强.城市物流中心单点选址模型及优化及方案评选［J］.辽宁工程技术大学学报:自然科学版，2010，29(4):690－693.REN Yong-chang，XING chao，ZHAO Guo-qiang.Optimization on single location selection of city logistics centre model and scheme selection［J］.Journal of Liaoning Technical University:Natural Science，2010，29(4):690－693.

［2］周爱莲，李旭宏，毛海军.企业物流中心稳健性选址模型［J］.交通运输工程学报，2010，10(4):60－65.ZHOU Ai-lian，LIXu-hong，MAO Hai-jun.Robusth location model of enterprise logistics center［J］.Journal of Traffic and Transportation Engineering，2010，10(4):60－65.

［3］Killmer K A.Sitting noxious facilities under uncertainty［J］.European Journal of Operational Research，2001，133:569－607.

［4］Feng Pan，Rakesh Nagi.Robust supply chain design under uncertain demand in agile manufacturing［J］.Computers＆Operations Research，2010(37):668－683.

［5］崔亚琼.综合因素条件下的物流中心选址研究［J］.铁道运输与经济，2010，32(10):53－57.CUIYa-qiong.Research on location selection of logistic center under comprehensive factors［J］.Railway Transport and Economy，2010，32(10):53－57.

［6］董龙云，史 峰，秦 进，等.区域交通物流基础设施可持续发展水平的多层次灰色综合评价［J］.铁道科学与工程学报，2009，2(6):64－68.DONG Long-yun，SHIFeng，QIN Jin，etal.Multi－level grey comprehensive evaluation for sustainable development level of regional transportation and logistics infrastructures［J］.Journal of Railway Science and Engineering，2009，2(6):64－68.

［7］Zhiqiang Lu，Nathalie Bostel.A facility location model for logistics systems including reverse flows:The case of remanufacturing activities［J］.Computers＆Operations Research，2007(34):299－323.

［8］Anshuman G，Maranas C D.Managing demand uncertainty in supply chain planning［J］.Computers and Chemical Engineering，2003(27):1219－1227.