集对社会网络分析模型及其应用

张春英,梁瑞涛,刘璐

(河北联合大学理学院,河北唐山063009)

0 引 言

社会网络又称人际网络,是由某些特定群体(人、企业、组织)相互的关系组成的相对稳定的关系网[1]。社会网络作为一种较新的数据挖掘技术,在管理、犯罪组织、互联网等领域都得到了广泛的应用[2,3,4]。文献[2,3,4]以社会网络为视角进行研究,找出网络中个体存在的各种社会关系,针对社会关系进行网络的信息挖掘。我国学者周卫国[5]等利用社会网络找出网站中用户之间的朋友关系,通过开发社会网络可视化平台挖掘用户之间的关联关系并找出用户之间的最短路径。学者高鹏[6]通过分析聊天数据的时序关系推断出用户间的社会网络关系,然后根据社会网络中反映出的用户交流关系判断并过滤了聊天数据中的噪声。文献[5,6]通过个体之间的引用、交流等一些个体相同的信息来发现网络中个体之间的关联关系,且利用社会网络从大量信息当中挖掘出有效信息。然而,在利用社会网络对网络中个体间的社会关系进行评估的过程中,个体之间还存在着不相同、不确定的信息元素,只利用确定的相同信息评估不能全面地反应网络中个体之间的关系。同时,在现实社会网络中节点和连接的属性常随时间动态变化[7],网络中节点关系也会随着各种因素的变化而发生变化,因此,只考虑网络中个体之间相同元素某个时刻的静态特征是很难进行准确的信息挖掘的。集对分析是由我国学者赵克勤[8]在1989年提出的一种处理不确定问题的系统分析方法。随后由我国学者孙晋众[9]等建立了一种基于马尔科夫链的集对分析的动态模型,从而使集对分析在处理动态不确定问题上有很大的进展。因此,本文基于集对分析理论,试图将集对分析的思想融入到社会网络中提出了集对社会网络分析模型、集对社会网络动态变化以及相关性质,通过简单例子的实现了集对社会网络的应用。

1 基本概念

1.1 社会网络

社会网络[10]可以表示为由多个点(社会行动者)和各点之间的连线(代表行动者之间的关系)组成的集合,若令G为一个社会网络,E为边集,V为点集,则社会网络可以表示为G=(V,E)。社会网络体现着一种结构关系,可反映行动者之间的社会关系。不同类型的关系形成了不同的社会网络。如社会交际网、社会支持网、讨论网、权利网等。

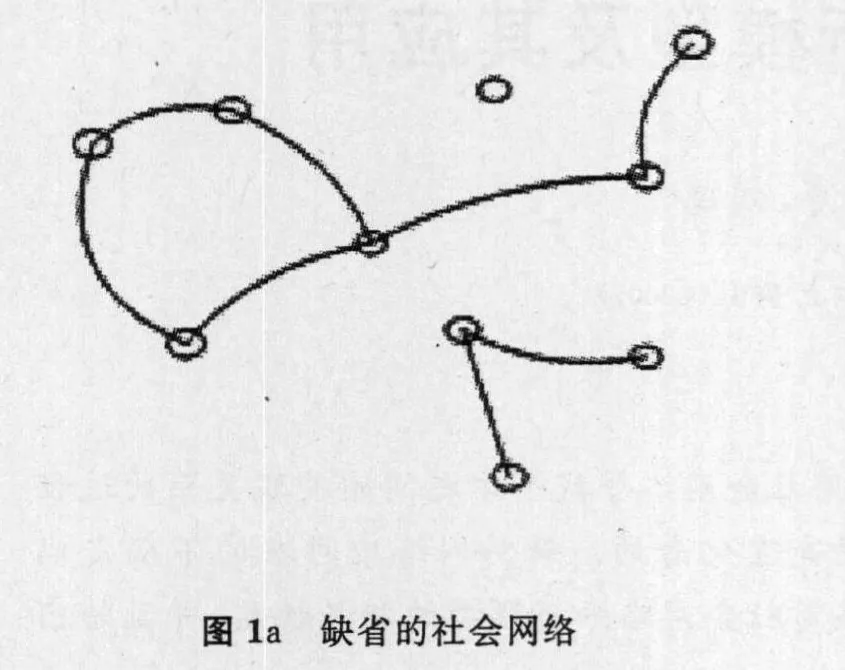
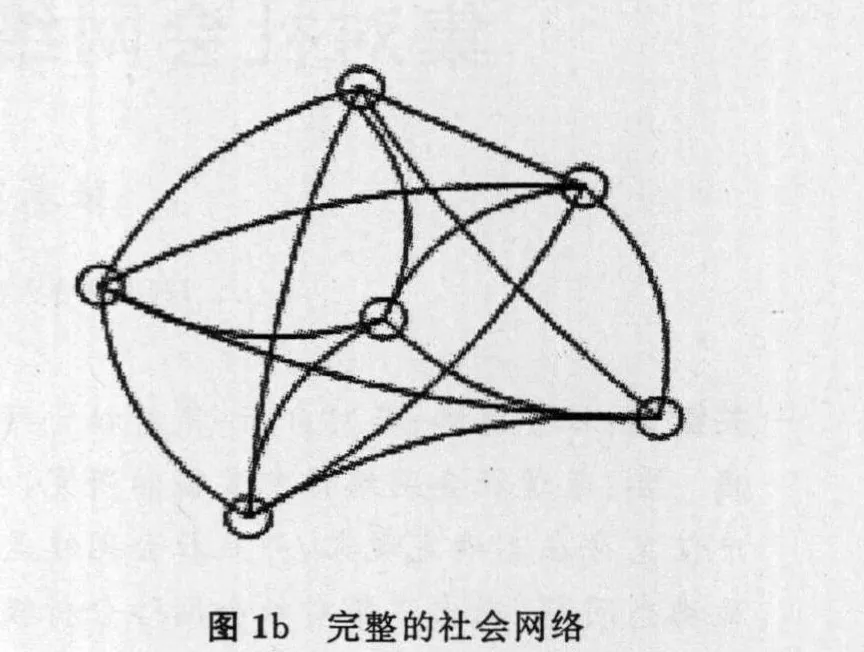
社会网络可以分为两类:(1)缺省的社会网络(defau lt social network):社会网络中行动者之间的信息存在不完备的;行动者与行动者之间的关系值是缺省的;(如图1a)(2)完整的社会网络(comp lete social network):行动者与行动者之间的关系值是完备的,也就是任意的两个行动者之间都有关系的存在。(如图1b)。

1.2 集对分析理论

定义1.1集对[8](set pair)就是由一定联系的两个集合构成对子,在协同的不确定系统背景下,对于两个有联系的集合A和B,对他们所具有的特性展开分析,共得到N个特性,其中S个为集对中共有的,并且有P个特性相对立(相反的),在其余F个特性上关系是不确定的,则两个集合联系度u的数学表达式为:

其中,i为差异标记,在区间[-1,1]上视不同情况取值,在[0,1]时差异部分趋向同一,在[-1,0]时差异部分趋向相反的。j仅起标记作用,集对所要处理的是任意两个集合之间由于不确定引起差异性,利用联系度表示出两个集合的关联程度。

1.3 联系度i的确定

在集对分析理论发展的今天,后继者都在不断完善集对分析理论,尤其在对i的取值上,赵克勤采用顺势取值法、逆势取值法、计算取值法和随机取值法等多种方法对i进行求解,提出应该在具体问题中找到i变化的规律[8],朱兵[11]等提出了用统计试验方法来确定差异不确定系数i的新途径,给出了合理的取值。但这些方法并未从根本上提出有效的方法。而由李陶[12]提出分别将差异度与同一度和对立度的关联度作为i的取值,运用灰色理论中的绝对关联度计算方法对i进行求解。这个方法更能够通过差异度、同一度、对立度给出更合理的取值。

2 集对社会网络分析模型

在社会网络关系中,对于两个研究对象的属性集合ek和es,共有N个属性(即两个对象的属性之和),其中有S为两个对象属性集合中属性中相同的属性,有P为两个对象属性集合中不相同的属性,有F为两个对象属性集合中不确定的属性。则令

针对社会网络中节点的复杂性,以及节点间关系的不确定性。我们给出了如下定义:

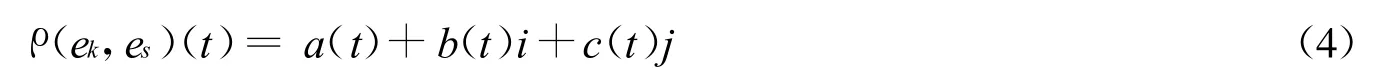
其中ek(t)∈U和es(t)∈U,a为两个对象所具有的相同属性与两个对象所共有的属性之比;b为两个对象所具有的不确定属性与两个对象所共有的属性之比;c为两个对象所具有的不相同的属性与两个对象所共有的属性之比;i为差异标记,在区间[-1,1]上视不同情况取值,j仅起标记作用,取值为-1。

由定义3.1我们知道在t时刻的两个研究对象的联系度为:

其中i∈[-1,1];j=-1;a+b+c=1

而在社会网络中,网络会随时间不断的变化,原有的属性值就会发生变化,有的属性值不变,有的转化为其他的属性。不妨设在t+1时刻,原有的St属性中仍有S t1个处于不变状态,St2个转化为不确定的属性, St3个转化为相反的属性。则St在[t,t+1]内的转移向量(经归一化处理)为

因此,在[t,t+1]时间内的转移矩阵为M,在t+1时刻,两个研究对象的联系度为ρ(ek,es)(t+1)为:

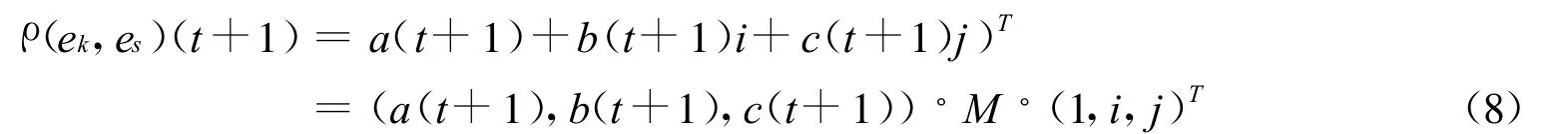
定义3.2:设矩阵R=(ρ(ek,es))k×s则称R为集对联系矩阵,其中ρ(ek,es)为集对联系矩阵中的元素,R =(ρ(ek,es))k×s表示研究对象ek与研究对象es的联系关系矩阵,或者说一个集对联系矩阵确定网络内各研究对象的联系度。此矩阵可表示为:

我们可以对集对社会网络的联系程度以及网络中心度问题给出如下定义:

定义3.3对于一个社会网络G=(V,E),则整个社会网络关系的集对联系密度为:

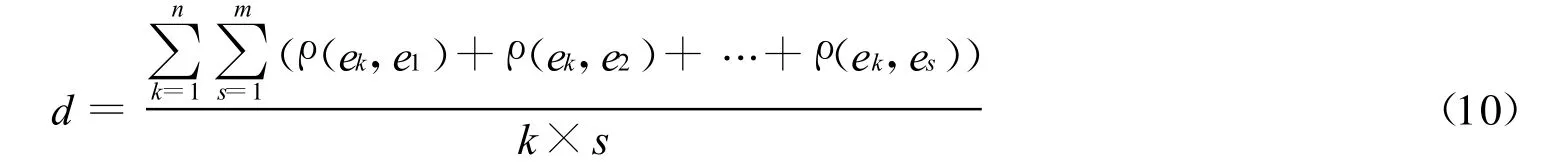
定义3.4:从社会网络关系中任一研究对象与其他研究对象的联系度之和取最大值与任意两个研究对象的联系度的差值比上差值中取最大值就是中心测度:

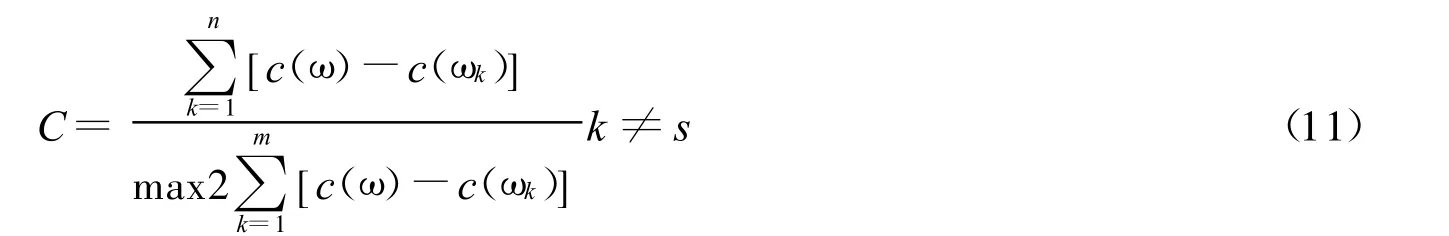
3 集对社会网络的性质

集对联系矩阵性质:在社会网络中任意两个研究对象之间的联系度为ρ(ek,es),则这个社会网络研究对象之间的关系组成一个集对联系矩阵。如图(5*5的网络)

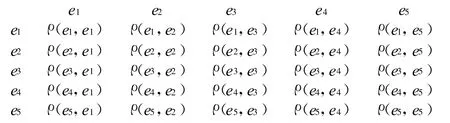
图2

由图2可知:

(1)集对联系矩阵任意的ρ(ek,es)有ρ(ek,es)=ρ(es,ek),表示研究对象ek和研究对象es的联系度与研究对象es和研究对象ek联系度相同。

(2)对角线上的值为常量,即ρ(ek,es)=1,表示对研究对象自身的同一度为1.,差异度和对立度为0。

(3)当ρ(ek,es)=-1时,则两个研究对象之间没有联系。

在社会网络关系中,任意两个研究对象之间的联系度随时间的变化也在发生的变化,两个研究对象之间的关系可能会加强,或者两个研究对象之间的关系可能会减弱。因此,当两个研究对象之间的联系度随时间变大或变小的话,两个研究对象之间的关系就会出现趋强或趋弱。如图3所示。

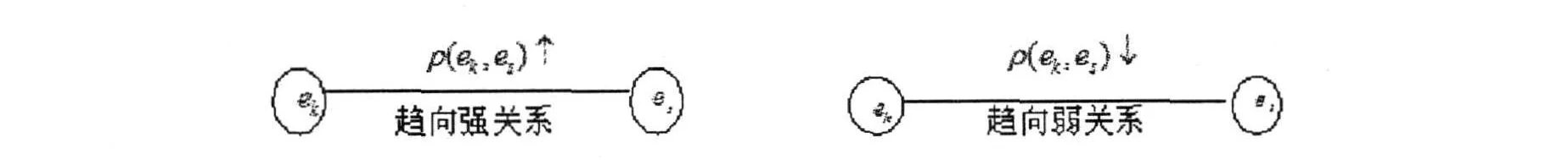
图3

定理1:在集对社会网络动态变化过程中:

若ρ(ek,es)逐渐增大达到某一稳定值时,则两个研究对象之间的关系就会趋于强关系。

若ρ(ek,es)逐渐减小达到某一稳定值时,则两个研究对象之间的关系就会趋于弱关系。

4 应用实例

社会网络分析对挖掘隐藏在确定的社会网络关系内的有效的方法,而实际的社会为网络环境里,有联系的研究对象之间关系属性特性上也存在着不确定性,由此我们提出了集对网络分析的概念,使我们不仅仅局限于0～1的二值网络关系之中,而有他们之间固有的属性特性造成网络关系中关系布局。因此,我们应该怎么样运用集对网络分析对网络进行分析挖掘呢?因此提出了集对网络分析的具体分析步骤:

Step1:在一个关系网络里,构造网络里每个研究对象的关系属性集合。按照集对的多种特性进行同一度、差异度和对立度分析,得到一组同一度 、差异度b和对立度c的量化值

Step2:采用灰色理论中的绝对关系度计算方法,计算联系度i的值。

Step3:根据计算出来的i的值,得到网络中任意两个研究对象的联系度ρ(ei,ej)(t)的值。

Step4:由step3得到的任意两个研究对象的联系度,从而构造集联矩阵M 。

Step5:由集联矩阵M计算网络的中心度测度C。找出网络中处于核心的研究对象。

Step6:提出结论,由网络的中心度情况给出整个网络的现在情况。

例:

由图建立集对网络模型

A={A,B,C}B={A,B,C}C={A,B,C,D}D={C,D,E,F}E={D,E,F}

F={D,E,F}任意两个研究对象的联系度为ρ(A,B)(t)ρ(A,C)(t)等。

采用灰色理论中的绝对关系度计算方法,计算可得i=0.770

构建集联矩阵

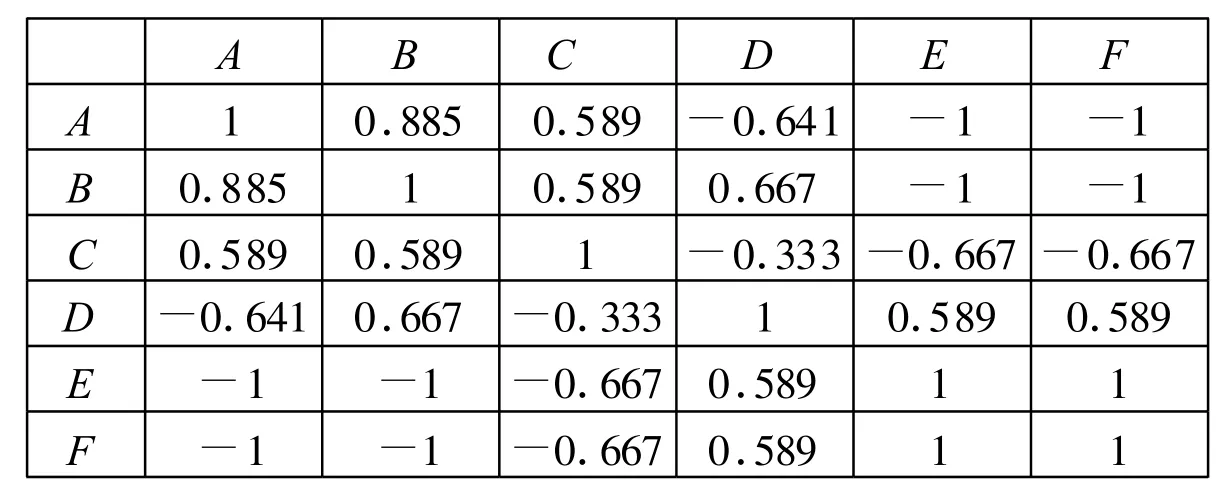
A B C D E F A 1 0.885 0.589 -0.641 -1 -1 B 0.885 1 0.589 0.667 -1 -1 C 0.589 0.589 1 -0.333-0.667-0.667 D -0.641 0.667 -0.333 1 0.589 0.589 E -1 -1 -0.667 0.589 1 1 F -1 -1 -0.667 0.589 1 1

通过计算D点的联系度最高,所以D的是简单网络的核心,中心测度为C=0.403。

5 结 语

本文首先提出了社会网络和集对分析的相关概念,对集对社会网络的定义的提出给出了有力的支持,同时根据集对社会网络的定义、网络的动态变化提出集对社会网络的相关性质,对解决社会网路中的不确定的问题以及网络的动态问题提出了新的方法。现在的集对社会网络理论还不太完善,还有许多工作需要完成。

[1] Gou H ong-mei,Huang Bi-qing.A framew ork for virtualen terprise Operationmanagement[J].Compu ters in Industry,2003,50(3): 333～352.

[2] 潘虹,翟东升.基于社会网络的信任模型研究[J].计算机工程与应用,2008,44(12),215～220.

[3] 卢志国,马国栋,任树怀.社会网络在美国大学图书馆的应用分析[J].图书馆工作与研究,2009,155(1),69～72.

[4] 邱峰,叶新东.网络学习社区的社会网络研究[J].现代教育技术,2010,20(2),37～41.

[5] 周卫国,史戎坚,叶婷.基于Web2.0网站中社会网络的信息挖掘[J].微计算机信息,2009,25(2-3):146～147.

[6] 高鹏,曹先彬.基于社会网络的聊天数据噪声过滤[J].计算机工程,2008,34(5):166～168.

[7] Gao Lin,Liu Jiming,Zhang Shiwu,et a1.Discovering the Dynamics in a Social Mem ory Network[C]//Proc.of 2008 International Conference on Web Intelligence and Intelligent Agen t Technology.Sydney,Australia:[s,n],2008.

[8] 赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社2000:8～90.

[9] 孙晋众,陈世权.一种集对分析的动态模型及其应用[J].系统工程,2004,22(5),35～38.

[10] John Scott著,刘军译,等.社会网络分析法[M].重庆:重庆大学出版社,2007.

[11] 朱兵,王文圣,王红芳,等.集对分析中差异不确定系数的探讨[J].四川大学学报(工程科学版),2008,40(1):5～9.

[12] 李陶,付强,丁红.基于灰色关联度的集对分析差异系数研究[J].黑龙江水专学报,2010,37(1)97～99.